Difference between revisions of "The Cross Product"
| Line 1: | Line 1: | ||
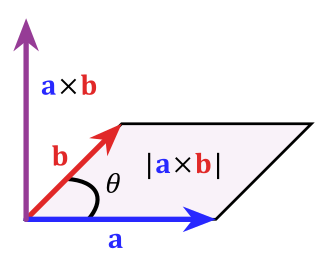
[[File:Cross product parallelogram.svg|thumb|Cross_product_parallelogram]] | [[File:Cross product parallelogram.svg|thumb|Cross_product_parallelogram]] | ||
| − | The cross product is an operation between two 3-dimensional vectors that returns a third vector orthogonal (i.e., perpendicular) to the first two. For vectors <math> \mathbf{u} = \langle u_1, u_2, u_3 \rangle </math> and <math> \mathbf{v} = \langle v_1, v_2, v_3 \rangle </math>, the cross product of <math> \mathbf{u} </math> and <math> \mathbf{v} </math> (notated as <math> u \times v </math>) is <math> \mathbf{w} = \langle u_2v_3 - u_3v_2, -(u_1v_3 - u_3v_1), u_1v_2 - u_2v_1 \rangle</math>. | + | The cross product is an operation between two 3-dimensional vectors that returns a third vector orthogonal (i.e., perpendicular) to the first two. For vectors <math> \mathbf{u} = \langle u_1, u_2, u_3 \rangle </math> and <math> \mathbf{v} = \langle v_1, v_2, v_3 \rangle </math>, the cross product of <math> \mathbf{u} </math> and <math> \mathbf{v} </math> (notated as <math> \mathbf{u} \times \mathbf{v} </math>) is <math> \mathbf{w} = \langle u_2v_3 - u_3v_2, -(u_1v_3 - u_3v_1), u_1v_2 - u_2v_1 \rangle</math>. |
One way to remember the cross product of <math> \mathbf{u} </math> and <math> \mathbf{v} </math> is to calculate it with the following determinant: | One way to remember the cross product of <math> \mathbf{u} </math> and <math> \mathbf{v} </math> is to calculate it with the following determinant: | ||
Revision as of 17:31, 20 September 2021
The cross product is an operation between two 3-dimensional vectors that returns a third vector orthogonal (i.e., perpendicular) to the first two. For vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u} = \langle u_1, u_2, u_3 \rangle } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v} = \langle v_1, v_2, v_3 \rangle } , the cross product of and (notated as ) is . One way to remember the cross product of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u} } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v} } is to calculate it with the following determinant:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{w} = \textrm{det}\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ u_1 & u_2 & u_3\\ v_1 & v_2 & v_3\\ \end{vmatrix} = (u_2v_3 - u_3v_2)\mathbf{i} - (u_1v_3 - u_3v_1)\mathbf{j} + (u_1v_2 - u_2v_1)\mathbf{k} }
Resources
- The Cross Product, OpenStax
- Cross Product, Cornell University