Difference between revisions of "Applications of Integrals"
| (4 intermediate revisions by one other user not shown) | |||
| Line 72: | Line 72: | ||
&=2\pi R^3-\frac{2\pi}{3}R^3=\frac{4\pi}{3}R^3 | &=2\pi R^3-\frac{2\pi}{3}R^3=\frac{4\pi}{3}R^3 | ||
\end{align}</math> | \end{align}</math> | ||
| + | |||
| + | ==Arc length== | ||
| + | Suppose that <math>f'</math> is continuous on <math>[a,b]</math> . Then the length of the curve given by <math>y=f(x)</math> between <math>a</math> and <math>b</math> is given by | ||
| + | :<math>L=\int\limits_a^b \sqrt{1+f'(x)^2}dx</math> | ||
| + | And in Leibniz notation | ||
| + | :<math>L=\int\limits_a^b \sqrt{1+\left(\tfrac{dy}{dx}\right)^2}dx</math> | ||
| + | |||
| + | '''Proof:''' Consider <math>y_{i+1}-y_i=f(x_{i+1})-f(x_i)</math> . By the Mean Value Theorem there is a point <math>z_i</math> in <math>(x_{i+1},x_i)</math> such that | ||
| + | :<math>y_{i+1}-y_i=f(x_{i+1})-f(x_i)=f'(z_i)(x_{i+1}-x_i)</math> | ||
| + | |||
| + | So | ||
| + | :{| | ||
| + | |<math>\bigl|P_iP_{i+1}\bigr|</math> | ||
| + | |<math>=\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\sqrt{(x_{i+1}-x_i)^2+f'(z_i)^2(x_{i+1}-x_i)^2}</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\sqrt{\bigl(1+f'(z_i)^2\bigr)(x_{i+1}-x_i)^2}</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\sqrt{1+f'(z_i)^2}\Delta x</math> | ||
| + | |} | ||
| + | |||
| + | Putting this into the definition of the length of <math>C</math> gives | ||
| + | |||
| + | :<math>L=\lim_{n\to\infty}\sum_{i=0}^{n-1}\sqrt{1+f'(z_i)^2}\Delta x</math> | ||
| + | |||
| + | Now this is the definition of the integral of the function <math>g(x)=\sqrt{1+f'(x)^2}</math> between <math>a</math> and <math>b</math> (notice that <math>g</math> is continuous because we are assuming that <math>f'</math> is continuous). Hence | ||
| + | |||
| + | :<math>L=\int\limits_a^b \sqrt{1+f'(x)^2}dx</math> | ||
| + | |||
| + | as claimed. | ||
| + | |||
| + | ===Example=== | ||
| + | Length of the curve <math>y=2x</math> from <math>x=0</math> to <math>x=1</math>}} | ||
| + | As a sanity check of our formula, let's calculate the length of the "curve" <math>y=2x</math> from <math>x=0</math> to <math>x=1</math> . First let's find the answer using the Pythagorean Theorem. | ||
| + | :<math>P_0=(0,0)</math> | ||
| + | and | ||
| + | :<math>P_1=(1,2)</math> | ||
| + | so the length of the curve, <math>s</math> , is | ||
| + | :<math>s=\sqrt{2^2+1^2}=\sqrt5</math> | ||
| + | Now let's use the formula | ||
| + | :<math>s=\int\limits_0^1 \sqrt{1+\left(\tfrac{d(2x)}{dx}\right)^2}\,dx=\int\limits_0^1 \sqrt{1+2^2}\,dx=\sqrt5x\bigg|_0^1=\sqrt5</math> | ||
==Resources== | ==Resources== | ||
| − | * [https:// | + | * [https://www.youtube.com/watch?v=FE0eJGdWC04 Business Calculus: Application of definite integral], Rajendra Dahal (YouTube) |
| − | |||
* [https://tutorial.math.lamar.edu/classes/calci/intappsintro.aspx Applications of Integrals - Cal I], Paul's Online Notes | * [https://tutorial.math.lamar.edu/classes/calci/intappsintro.aspx Applications of Integrals - Cal I], Paul's Online Notes | ||
* [https://tutorial.math.lamar.edu/classes/calcii/intappsintro.aspx Applications of Integrals - Cal II], Paul's Online Notes | * [https://tutorial.math.lamar.edu/classes/calcii/intappsintro.aspx Applications of Integrals - Cal II], Paul's Online Notes | ||
| + | |||
| + | ==Licensing== | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Area Area, Wikibooks: Calculus] under a CC BY-SA license | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Volume Volume, Wikibooks: Calculus] under a CC BY-SA license | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Arc_length Arc length, Wikibooks: Calculus] under a CC BY-SA license | ||
Latest revision as of 15:23, 28 October 2021
Contents
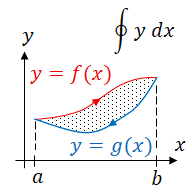
Area between two curves
Suppose we are given two functions and and we want to find the area between them on the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} . Also assume that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)\ge g(x)} for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} on the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} . Begin by partitioning the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} into Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} equal subintervals each having a length of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x=\frac{b-a}{n}} . Next choose any point in each subinterval, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i^*} . Now we can 'create' rectangles on each interval. At the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i*} , the height of each rectangle is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_i^*)-g(x_i^*)} and the width is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} . Thus the area of each rectangle is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigl[f(x_i^*)-g(x_i^*)\bigr]\Delta x} . An approximation of the area, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} , between the two curves is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A:=\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x} .
Now we take the limit as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} approaches infinity and get
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x}
which gives the exact area. Recalling the definition of the definite integral we notice that
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\int\limits_a^b \bigl(f(x)-g(x)\bigr)dx} .
This formula of finding the area between two curves is sometimes known as applying integration with respect to the x-axis since the rectangles used to approximate the area have their bases lying parallel to the x-axis. It will be most useful when the two functions are of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1=f(x)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_2=g(x)} . Sometimes however, one may find it simpler to integrate with respect to the y-axis. This occurs when integrating with respect to the x-axis would result in more than one integral to be evaluated. These functions take the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=f(y)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=g(y)} on the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [c,d]} . Note that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [c,d]} are values of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} . The derivation of this case is completely identical. Similar to before, we will assume that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y)\ge g(y)} for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [c,d]} . Now, as before we can divide the interval into Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} subintervals and create rectangles to approximate the area between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(y)} . It may be useful to picture each rectangle having their 'width', Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta y} , parallel to the y-axis and 'height', Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y_i^*)-g(y_i^*)} at the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_i^*} , parallel to the x-axis. Following from the work above we may reason that an approximation of the area, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} , between the two curves is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A:=\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y} .
As before, we take the limit as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} approaches infinity to arrive at
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y} ,
which is nothing more than a definite integral, so
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\int\limits_c^d \bigl(f(y)-g(y)\bigr)dy} .
Regardless of the form of the functions, we basically use the same formula.
Volume
If the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)} is continuous on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} , then the volume Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_S} of the solid Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is given by:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_S=\int\limits_a^b A(x)dx}
Example 1: A right cylinder
Now we will calculate the volume of a right cylinder using our new ideas about how to calculate volume. Since we already know the formula for the volume of a cylinder this will give us a "sanity check" that our formulas make sense. First, we choose a dimension along which to integrate. In this case, it will greatly simplify the calculations to integrate along the height of the cylinder, so this is the direction we will choose. Thus we will call the vertical direction Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} (see Figure 1). Now we find the function, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)} , which will describe the cross-sectional area of our cylinder at a height of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . The cross-sectional area of a cylinder is simply a circle. Now simply recall that the area of a circle is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi r^2} , and so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)=\pi r^2} . Before performing the computation, we must choose our bounds of integration. In this case, we simply define Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} to be the base of the cylinder, and so we will integrate from to , where is the height of the cylinder. Finally, we integrate:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} V_{\mathrm{cylinder}}&=\int\limits_a^b A(x)dx\\ &=\int\limits_0^h\pi r^2dx\\ &=\pi r^2\int\limits_0^hdx\\ &=\pi r^2x\bigg|_{x=0}^h\\ &=\pi r^2(h-0)\\ &=\pi r^2h\end{align}}
This is exactly the familiar formula for the volume of a cylinder.
Example 2: A right circular cone
For our next example we will look at an example where the cross sectional area is not constant. Consider a right circular cone. Once again the cross sections are simply circles. But now the radius varies from the base of the cone to the tip. Once again we choose Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} to be the vertical direction, with the base at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} and the tip at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=h} , and we will let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} denote the radius of the base. While we know the cross sections are just circles we cannot calculate the area of the cross sections unless we find some way to determine the radius of the circle at height Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .
Luckily in this case it is possible to use some of what we know from geometry. We can imagine cutting the cone perpendicular to the base through some diameter of the circle all the way to the tip of the cone. If we then look at the flat side we just created, we will see simply a triangle, whose geometry we understand well. The right triangle from the tip to the base at height Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is similar to the right triangle from the tip to the base at height Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} . This tells us that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{r}{h-x}=\frac{R}{h}} . So that we see that the radius of the circle at height Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(x)=\frac{R}{h}(h-x)} . Now using the familiar formula for the area of a circle we see that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)=\pi\frac{R^2}{h^2}(h-x)^2} .
Now we are ready to integrate.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} V_{\mathrm{cone}}&=\int\limits_a^b A(x)dx\\ &=\int\limits_0^h \pi\frac{R^2}{h^2}(h-x)^2dx\\ &=\pi\frac{R^2}{h^2}\int\limits_0^h(h-x)^2dx \end{align}}
By u-substitution we may let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=h-x} , then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle du=-dx} and our integral becomes
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} &&=\pi\frac{R^2}{h^2}\left(-\int\limits_h^0 u^2du\right)\\ &&=\pi\frac{R^2}{h^2}\left(-\frac{u^3}{3}\bigg|_h^0\right)\\ &&=\pi\frac{R^2}{h^2}\left(-0+\frac{h^3}{3}\right)\\ &&=\frac{\pi}{3}R^2h \end{align}}
Example 3: A sphere

In a similar fashion, we can use our definition to prove the well known formula for the volume of a sphere. First, we must find our cross-sectional area function, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)} . Consider a sphere of radius Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} which is centered at the origin in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^3} . If we again integrate vertically then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} will vary from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -R} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} . In order to find the area of a particular cross section it helps to draw a right triangle whose points lie at the center of the sphere, the center of the circular cross section, and at a point along the circumference of the cross section. As shown in the diagram the side lengths of this triangle will be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x|} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} . Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} is the radius of the circular cross section. Then by the Pythagorean theorem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\sqrt{R^2-|x|^2}} and find that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)=\pi(R^2-|x|^2)} . It is slightly helpful to notice that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x|^2=x^2} so we do not need to keep the absolute value.
So we have that
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} V_{\mathrm{sphere}}&=\int\limits_a^b A(x)dx\\ &=\int\limits_{-R}^R\pi(R^2-x^2)dx\\ &=\pi\int\limits_{-R}^R R^2dx-\pi\int\limits_{-R}^R x^2dx\\ &=\pi R^2x\Bigg|_{-R}^R-\pi\frac{x^3}{3}\Bigg|_{-R}^R\\ &=\pi R^2(R-(-R))-\pi\left(\frac{R^3}{3}-\frac{(-R)^3}{3}\right)\\ &=2\pi R^3-\frac{2\pi}{3}R^3=\frac{4\pi}{3}R^3 \end{align}}
Arc length
Suppose that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'} is continuous on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} . Then the length of the curve given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=f(x)} between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} is given by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=\int\limits_a^b \sqrt{1+f'(x)^2}dx}
And in Leibniz notation
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=\int\limits_a^b \sqrt{1+\left(\tfrac{dy}{dx}\right)^2}dx}
Proof: Consider Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{i+1}-y_i=f(x_{i+1})-f(x_i)} . By the Mean Value Theorem there is a point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_i} in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_{i+1},x_i)} such that
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{i+1}-y_i=f(x_{i+1})-f(x_i)=f'(z_i)(x_{i+1}-x_i)}
So
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigl|P_iP_{i+1}\bigr|} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{(x_{i+1}-x_i)^2+f'(z_i)^2(x_{i+1}-x_i)^2}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{\bigl(1+f'(z_i)^2\bigr)(x_{i+1}-x_i)^2}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{1+f'(z_i)^2}\Delta x}
Putting this into the definition of the length of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} gives
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=\lim_{n\to\infty}\sum_{i=0}^{n-1}\sqrt{1+f'(z_i)^2}\Delta x}
Now this is the definition of the integral of the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x)=\sqrt{1+f'(x)^2}} between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} (notice that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} is continuous because we are assuming that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'} is continuous). Hence
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=\int\limits_a^b \sqrt{1+f'(x)^2}dx}
as claimed.
Example
Length of the curve Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=2x} from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=1} }} As a sanity check of our formula, let's calculate the length of the "curve" Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=2x} from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=1} . First let's find the answer using the Pythagorean Theorem.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_0=(0,0)}
and
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_1=(1,2)}
so the length of the curve, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} , is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=\sqrt{2^2+1^2}=\sqrt5}
Now let's use the formula
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=\int\limits_0^1 \sqrt{1+\left(\tfrac{d(2x)}{dx}\right)^2}\,dx=\int\limits_0^1 \sqrt{1+2^2}\,dx=\sqrt5x\bigg|_0^1=\sqrt5}
Resources
- Business Calculus: Application of definite integral, Rajendra Dahal (YouTube)
- Applications of Integrals - Cal I, Paul's Online Notes
- Applications of Integrals - Cal II, Paul's Online Notes
Licensing
Content obtained and/or adapted from:
- Area, Wikibooks: Calculus under a CC BY-SA license
- Volume, Wikibooks: Calculus under a CC BY-SA license
- Arc length, Wikibooks: Calculus under a CC BY-SA license