Difference between revisions of "The Geometric Interpretation of the Determinant"
(Created page with "This parallelogram picture <center> x200px </center> is familiar from the construction of the sum of the two vectors. One way to compute the...") |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 34: | Line 34: | ||
is no coincidence. | is no coincidence. | ||
| − | + | ||
| + | The properties in the definition of determinants | ||
make reasonable postulates for a function | make reasonable postulates for a function | ||
that measures the size of the region | that measures the size of the region | ||
| Line 98: | Line 99: | ||
justification to interpret <math> \det(\vec{v}_1,\dots,\vec{v}_n) </math> as the | justification to interpret <math> \det(\vec{v}_1,\dots,\vec{v}_n) </math> as the | ||
size of the box formed by the vectors. | size of the box formed by the vectors. | ||
| − | |||
| − | |||
| − | |||
| − | + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | |
| − | + | '''Example 1.1:''' | |
The volume of this parallelepiped, which can be found by the usual | The volume of this parallelepiped, which can be found by the usual | ||
formula from high school geometry, is <math>12</math>. | formula from high school geometry, is <math>12</math>. | ||
| Line 115: | Line 113: | ||
\end{vmatrix}=12</math> | \end{vmatrix}=12</math> | ||
</center> | </center> | ||
| − | + | </blockquote> | |
| − | + | ||
| − | + | '''Remark 1.2:''' | |
Although property (2) of the definition of | Although property (2) of the definition of | ||
determinants is redundant, it raises an important point. | determinants is redundant, it raises an important point. | ||
| Line 144: | Line 142: | ||
then the sign is positive. | then the sign is positive. | ||
Following a clockwise arc gives a negative sign. | Following a clockwise arc gives a negative sign. | ||
| − | + | ||
| + | The sign returned by the size function reflects the | ||
"orientation" or "sense" of the box. | "orientation" or "sense" of the box. | ||
(We see the same thing if we picture the effect of scalar multiplication | (We see the same thing if we picture the effect of scalar multiplication | ||
by a negative scalar.) | by a negative scalar.) | ||
| − | Although it is both interesting and important, the idea of orientation turns out to be tricky. It is not needed for the development below, and so we will pass it by. | + | Although it is both interesting and important, the idea of orientation turns out to be tricky. It is not needed for the development below, and so we will pass it by. |
| − | + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | |
| − | + | '''Definition 1.3:''' | |
| − | |||
| − | |||
The '''box''' (or '''parallelepiped''') formed by <math> \langle | The '''box''' (or '''parallelepiped''') formed by <math> \langle | ||
\vec{v}_1,\dots,\vec{v}_n \rangle </math> (where each vector is from | \vec{v}_1,\dots,\vec{v}_n \rangle </math> (where each vector is from | ||
| Line 159: | Line 156: | ||
\{t_1\vec{v}_1+\dots+t_n\vec{v}_n \,\big|\, t_1,\ldots,t_n\in [0..1]\} | \{t_1\vec{v}_1+\dots+t_n\vec{v}_n \,\big|\, t_1,\ldots,t_n\in [0..1]\} | ||
</math>. The '''volume''' of a box is the absolute value of the | </math>. The '''volume''' of a box is the absolute value of the | ||
| − | determinant of the matrix with those vectors as columns. | + | determinant of the matrix with those vectors as columns. |
| + | </blockquote> | ||
| − | + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | |
| − | + | Example 1.4: | |
Volume, because it is an absolute value, | Volume, because it is an absolute value, | ||
does not depend on the order in which the vectors are given. | does not depend on the order in which the vectors are given. | ||
| − | The volume of the parallelepiped in | + | The volume of the parallelepiped in can also be computed as the absolute value of this determinant. |
| − | can also be computed as the absolute value of this determinant. | ||
:<math> | :<math> | ||
| Line 175: | Line 172: | ||
\end{vmatrix}=-12 | \end{vmatrix}=-12 | ||
</math> | </math> | ||
| − | + | </blockquote> | |
The definition of volume gives a geometric interpretation to | The definition of volume gives a geometric interpretation to | ||
| Line 182: | Line 179: | ||
spaces. | spaces. | ||
| − | + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | |
| − | + | ||
| + | '''Theorem 1.5:''' | ||
A transformation <math> t:\mathbb{R}^n\to \mathbb{R}^n </math> changes | A transformation <math> t:\mathbb{R}^n\to \mathbb{R}^n </math> changes | ||
the size of all boxes by the same factor, namely the size of the image | the size of all boxes by the same factor, namely the size of the image | ||
| Line 193: | Line 191: | ||
determinants | determinants | ||
<math>\left|TS\right|=\left|T\right|\cdot\left|S\right|</math>. | <math>\left|TS\right|=\left|T\right|\cdot\left|S\right|</math>. | ||
| − | + | </blockquote> | |
The two sentences state the same idea, first in map terms and then | The two sentences state the same idea, first in map terms and then | ||
| Line 200: | Line 198: | ||
the second sentence, the matrix version, is more convienent for the proof | the second sentence, the matrix version, is more convienent for the proof | ||
and is also the way that we shall use this result later. | and is also the way that we shall use this result later. | ||
| − | |||
| − | |||
| − | |||
| − | + | '''Proof:''' | |
| − | |||
The two statements are equivalent because | The two statements are equivalent because | ||
<math>\left|t(S)\right|=\left|TS\right|</math>, as both give the size of the box that is the | <math>\left|t(S)\right|=\left|TS\right|</math>, as both give the size of the box that is the | ||
| Line 232: | Line 226: | ||
If the elementary matrix <math>E</math> is <math>M_i(k)</math> then <math>M_i(k)S</math> equals <math>S</math> except that row <math>i</math> has been multiplied by <math>k</math>. The third property of determinant functions then gives that <math>\left|M_i(k)S\right|=k\cdot\left|S\right|</math>. But <math>\left|M_i(k)\right|=k</math>, again by the third property because <math>M_i(k)</math> is derived from the identity by multiplication of row <math>i</math> by <math>k</math>, and so <math> \left|ES\right|=\left|E\right|\cdot\left|S\right| </math> holds for <math>E=M_i(k)</math>. The <math>E=P_{i,j}=-1</math> and <math>E=C_{i,j}(k)</math> checks are similar. | If the elementary matrix <math>E</math> is <math>M_i(k)</math> then <math>M_i(k)S</math> equals <math>S</math> except that row <math>i</math> has been multiplied by <math>k</math>. The third property of determinant functions then gives that <math>\left|M_i(k)S\right|=k\cdot\left|S\right|</math>. But <math>\left|M_i(k)\right|=k</math>, again by the third property because <math>M_i(k)</math> is derived from the identity by multiplication of row <math>i</math> by <math>k</math>, and so <math> \left|ES\right|=\left|E\right|\cdot\left|S\right| </math> holds for <math>E=M_i(k)</math>. The <math>E=P_{i,j}=-1</math> and <math>E=C_{i,j}(k)</math> checks are similar. | ||
| − | |||
| − | + | ||
| − | + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | |
| + | '''Example 1.6:''' | ||
Application of the map <math>t</math> represented with respect to the standard | Application of the map <math>t</math> represented with respect to the standard | ||
bases by | bases by | ||
| Line 264: | Line 258: | ||
\end{vmatrix}=6</math> | \end{vmatrix}=6</math> | ||
</center> | </center> | ||
| − | + | </blockquote> | |
| − | + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | |
| − | + | '''Corollary 1.7:''' | |
If a matrix is invertible then the determinant of its inverse is the inverse of its determinant <math>\left|T^{-1}\right|=1/\left|T\right|</math>. | If a matrix is invertible then the determinant of its inverse is the inverse of its determinant <math>\left|T^{-1}\right|=1/\left|T\right|</math>. | ||
| − | + | </blockquote> | |
| − | + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | |
| − | + | Proof: | |
<math>1=\left|I\right|=\left|TT^{-1}\right|=\left|T\right|\cdot\left|T^{-1}\right|</math> | <math>1=\left|I\right|=\left|TT^{-1}\right|=\left|T\right|\cdot\left|T^{-1}\right|</math> | ||
| − | + | </blockquote> | |
Recall that determinants are not additive homomorphisms, | Recall that determinants are not additive homomorphisms, | ||
| Line 282: | Line 276: | ||
<math>\det(AB)</math> does equal <math>\det(A)\cdot \det(B)</math>. | <math>\det(AB)</math> does equal <math>\det(A)\cdot \det(B)</math>. | ||
| − | == | + | == Licensing == |
| − | * [https://en.wikibooks.org/wiki/Linear_Algebra/Determinants_as_Size_Functions Determinants as Size Functions | + | Content obtained and/or adapted from: |
| + | * [https://en.wikibooks.org/wiki/Linear_Algebra/Determinants_as_Size_Functions Determinants as Size Functions, Wikibooks: Linear Algebra] under a CC BY-SA license | ||
Latest revision as of 14:27, 5 November 2021
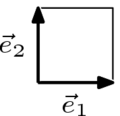
This parallelogram picture
is familiar from the construction of the sum of the two vectors. One way to compute the area that it encloses is to draw this rectangle and subtract the area of each subregion.
 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{l} \text{area of parallelogram} \\ \quad =\text{area of rectangle} -\text{area of }A-\text{area of }B \\ \qquad -\cdots-\text{area of }F \\ \quad =(x_1+x_2)(y_1+y_2)-x_2y_1-x_1y_1/2 \\ \qquad -x_2y_2/2-x_2y_2/2-x_1y_1/2-x_2y_1 \\ \quad =x_1y_2-x_2y_1 \end{array}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{l} \text{area of parallelogram} \\ \quad =\text{area of rectangle} -\text{area of }A-\text{area of }B \\ \qquad -\cdots-\text{area of }F \\ \quad =(x_1+x_2)(y_1+y_2)-x_2y_1-x_1y_1/2 \\ \qquad -x_2y_2/2-x_2y_2/2-x_1y_1/2-x_2y_1 \\ \quad =x_1y_2-x_2y_1 \end{array}}
The fact that the area equals the value of the determinant
is no coincidence.
The properties in the definition of determinants make reasonable postulates for a function that measures the size of the region enclosed by the vectors in the matrix.
For instance, this shows the effect of multiplying one of the box-defining vectors by a scalar (the scalar used is ).
The region formed by and is bigger, by a factor of , than the shaded region enclosed by and . That is, and in general we expect of the size measure that . Of course, this postulate is already familiar as one of the properties in the defintion of determinants.
Another property of determinants is that they are unaffected by pivoting. Here are before-pivoting and after-pivoting boxes (the scalar used is ).
Although the region on the right, the box formed by and , is more slanted than the shaded region, the two have the same base and the same height and hence the same area. This illustrates that . Generalized, , which is a restatement of the determinant postulate.
Of course, this picture
shows that , and we naturally extend that to any number of dimensions , which is a restatement of the property that the determinant of the identity matrix is one.
With that, because property (2) of determinants is redundant (as remarked right after the definition), we have that all of the properties of determinants are reasonable to expect of a function that gives the size of boxes. We can now cite the work done in the prior section to show that the determinant exists and is unique to be assured that these postulates are consistent and sufficient (we do not need any more postulates). That is, we've got an intuitive justification to interpret as the size of the box formed by the vectors.
Example 1.1: The volume of this parallelepiped, which can be found by the usual formula from high school geometry, is .
Remark 1.2:
Although property (2) of the definition of
determinants is redundant, it raises an important point.
Consider these two.

| 
|
The only difference between them is in the order in which the vectors are taken. If we take first and then go to , follow the counterclockwise arc shown, then the sign is positive. Following a clockwise arc gives a negative sign.
The sign returned by the size function reflects the "orientation" or "sense" of the box. (We see the same thing if we picture the effect of scalar multiplication by a negative scalar.)
Although it is both interesting and important, the idea of orientation turns out to be tricky. It is not needed for the development below, and so we will pass it by.
Definition 1.3: The box (or parallelepiped) formed by (where each vector is from ) includes all of the set . The volume of a box is the absolute value of the determinant of the matrix with those vectors as columns.
Example 1.4: Volume, because it is an absolute value, does not depend on the order in which the vectors are given. The volume of the parallelepiped in can also be computed as the absolute value of this determinant.
The definition of volume gives a geometric interpretation to something in the space, boxes made from vectors. The next result relates the geometry to the functions that operate on spaces.
Theorem 1.5: A transformation changes the size of all boxes by the same factor, namely the size of the image of a box is times the size of the box , where is the matrix representing with respect to the standard basis. That is, for all matrices, the determinant of a product is the product of the determinants .
The two sentences state the same idea, first in map terms and then in matrix terms. Although we tend to prefer a map point of view, the second sentence, the matrix version, is more convienent for the proof and is also the way that we shall use this result later.
Proof: The two statements are equivalent because , as both give the size of the box that is the image of the unit box under the composition (where is the map represented by with respect to the standard basis).
First consider the case that . A matrix has a zero determinant if and only if it is not invertible. Observe that if is invertible, so that there is an such that , then the associative property of matrix multiplication shows that is also invertible (with inverse ). Therefore, if is not invertible then neither is — if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|T\right|=0} then , and the result holds in this case.
Now consider the case that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|T\right|\neq 0} , that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} is nonsingular. Recall that any nonsingular matrix can be factored into a product of elementary matrices, so that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TS=E_1E_2\cdots E_rS} . In the rest of this argument, we will verify that if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is an elementary matrix then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|ES\right|=\left|E\right|\cdot\left|S\right| } . The result will follow because then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|TS\right|=\left|E_1\cdots E_rS\right|=\left|E_1\right|\cdots\left|E_r\right|\cdot\left|S\right| =\left|E_1\cdots E_r\right|\cdot\left|S\right|=\left|T\right|\cdot\left|S\right|} .
If the elementary matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_i(k)} then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_i(k)S} equals Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} except that row Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} has been multiplied by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} . The third property of determinant functions then gives that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|M_i(k)S\right|=k\cdot\left|S\right|} . But Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|M_i(k)\right|=k} , again by the third property because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_i(k)} is derived from the identity by multiplication of row Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , and so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|ES\right|=\left|E\right|\cdot\left|S\right| } holds for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=M_i(k)} . The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=P_{i,j}=-1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=C_{i,j}(k)} checks are similar.
Example 1.6: Application of the map Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} represented with respect to the standard bases by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 &1 \\ -2 &0 \end{pmatrix} }
will double sizes of boxes, e.g., from this
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} 2 &1 \\ 1 &2 \end{vmatrix}=3}
to this
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} 3 &3 \\ -4 &-2 \end{vmatrix}=6}
Corollary 1.7: If a matrix is invertible then the determinant of its inverse is the inverse of its determinant Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|T^{-1}\right|=1/\left|T\right|} .
Proof: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=\left|I\right|=\left|TT^{-1}\right|=\left|T\right|\cdot\left|T^{-1}\right|}
Recall that determinants are not additive homomorphisms, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(A+B)} need not equal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(A)+\det(B)} . The above theorem says, in contrast, that determinants are multiplicative homomorphisms: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(AB)} does equal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det(A)\cdot \det(B)} .
Licensing
Content obtained and/or adapted from:
- Determinants as Size Functions, Wikibooks: Linear Algebra under a CC BY-SA license





























![{\displaystyle \{t_{1}{\vec {v}}_{1}+\dots +t_{n}{\vec {v}}_{n}\,{\big |}\,t_{1},\ldots ,t_{n}\in [0..1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f9a540e9629e8fb4043860c340547644394e678)




















