Difference between revisions of "Theorem:Bolzano-Weierstrass"
| (2 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
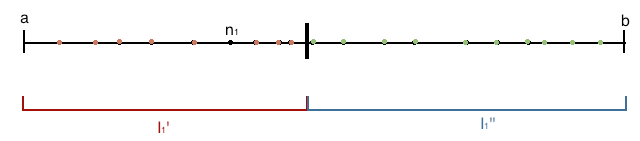
<li><strong>Proof 1:</strong> Let <span class="math-inline"><math>(a_n)</math></span> be a bounded sequence, that is the set <span class="math-inline"><math>\{ a_n : n \in \mathbb{N} \}</math></span> is bounded. Suppose that <span class="math-inline"><math>a</math></span> is a lower bound for this set, and <span class="math-inline"><math>b</math></span> is an upper bound for this set, and so <span class="math-inline"><math>a \leq a_n \leq b_n</math></span> for all <span class="math-inline"><math>n \in \mathbb{N}</math></span>. Therefore the set <span class="math-inline"><math>\{ a_n : n \in \mathbb{N} \}</math></span> is contained in the interval <span class="math-inline"><math>I_1 = [a, b]</math></span>.</li> | <li><strong>Proof 1:</strong> Let <span class="math-inline"><math>(a_n)</math></span> be a bounded sequence, that is the set <span class="math-inline"><math>\{ a_n : n \in \mathbb{N} \}</math></span> is bounded. Suppose that <span class="math-inline"><math>a</math></span> is a lower bound for this set, and <span class="math-inline"><math>b</math></span> is an upper bound for this set, and so <span class="math-inline"><math>a \leq a_n \leq b_n</math></span> for all <span class="math-inline"><math>n \in \mathbb{N}</math></span>. Therefore the set <span class="math-inline"><math>\{ a_n : n \in \mathbb{N} \}</math></span> is contained in the interval <span class="math-inline"><math>I_1 = [a, b]</math></span>.</li> | ||
</ul> | </ul> | ||
| − | + | ||
| + | [[File:Bolzano-Weierstrass 1.png|center|Bolzano-Weierstrass 1]] | ||
| + | |||
<ul> | <ul> | ||
<li>Let's take <span class="math-inline"><math>n_1 = 1</math></span>, i.e., let the first term of the subsequence <span class="math-inline"><math>(a_{n_k})</math></span> be equal to the first term of the parent sequence <span class="math-inline"><math>(a_n)</math></span>.</li> | <li>Let's take <span class="math-inline"><math>n_1 = 1</math></span>, i.e., let the first term of the subsequence <span class="math-inline"><math>(a_{n_k})</math></span> be equal to the first term of the parent sequence <span class="math-inline"><math>(a_n)</math></span>.</li> | ||
| Line 12: | Line 14: | ||
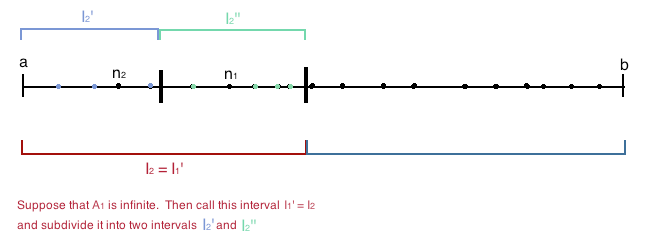
<li>We will now take the interval <span class="math-inline"><math>I_1</math></span> and divide into two subintervals of equal length. We will call these intervals <span class="math-inline"><math>I_1'</math></span> and <span class="math-inline"><math>I_1''</math></span>. We will also divide the set of indices into two sets. Let <span class="math-inline"><math>A_1 := \{ n \in \mathbb{N} : n > n_1, a_n \in I_1' \}</math></span> and let <span class="math-inline"><math>B_1 = \{ n \in \mathbb{N} : n > n_1, a_N \in I_1'' \}</math></span>. We note that <span class="math-inline"><math>A_1</math></span> is the set of indices <span class="math-inline"><math>n</math></span> greater than the first index in our subsequence, <span class="math-inline"><math>n_1</math></span>, such that <span class="math-inline"><math>a_n</math></span> is in the interval <span class="math-inline"><math>I_1'</math></span>. Similarly, <span class="math-inline"><math>B_1</math></span> is the set of indices <span class="math-inline"><math>n</math></span> greater than the first index in our subsequence, <span class="math-inline"><math>n_1</math></span> such that <span class="math-inline"><math>a_N</math></span> is in the interval <span class="math-inline"><math>I_1''</math></span>.</li> | <li>We will now take the interval <span class="math-inline"><math>I_1</math></span> and divide into two subintervals of equal length. We will call these intervals <span class="math-inline"><math>I_1'</math></span> and <span class="math-inline"><math>I_1''</math></span>. We will also divide the set of indices into two sets. Let <span class="math-inline"><math>A_1 := \{ n \in \mathbb{N} : n > n_1, a_n \in I_1' \}</math></span> and let <span class="math-inline"><math>B_1 = \{ n \in \mathbb{N} : n > n_1, a_N \in I_1'' \}</math></span>. We note that <span class="math-inline"><math>A_1</math></span> is the set of indices <span class="math-inline"><math>n</math></span> greater than the first index in our subsequence, <span class="math-inline"><math>n_1</math></span>, such that <span class="math-inline"><math>a_n</math></span> is in the interval <span class="math-inline"><math>I_1'</math></span>. Similarly, <span class="math-inline"><math>B_1</math></span> is the set of indices <span class="math-inline"><math>n</math></span> greater than the first index in our subsequence, <span class="math-inline"><math>n_1</math></span> such that <span class="math-inline"><math>a_N</math></span> is in the interval <span class="math-inline"><math>I_1''</math></span>.</li> | ||
</ul> | </ul> | ||
| − | + | ||
| + | [[File:Bolzano-Weierstrass 2.png|center|Bolzano-Weierstrass 2]] | ||
| + | |||
<ul> | <ul> | ||
<li>We note that both of the sets <span class="math-inline"><math>A_1</math></span> and <span class="math-inline"><math>B_1</math></span> cannot be finite since <span class="math-inline"><math>A_1</math></span> and <span class="math-inline"><math>B_1</math></span> contain all of the indices of the sequence <span class="math-inline"><math>(a_n)</math></span> which has infinitely many indices since it is an infinite sequence. If <span class="math-inline"><math>A_1</math></span> is infinite, then we let <span class="math-inline"><math>I_2 = I_1'</math></span>, and we will let <span class="math-inline"><math>n_2</math></span> be the smallest natural number index in the set <span class="math-inline"><math>A_1</math></span>, which we are ensured to have by the Well Ordering Principle. If <span class="math-inline"><math>A_1</math></span> is finite, then <span class="math-inline"><math>B_1</math></span> is infinite and we let <span class="math-inline"><math>I_2 = I_1''</math></span> and we let <span class="math-inline"><math>n_2</math></span> be the smallest natural number index in the set <span class="math-inline"><math>B_1</math></span>, which once again, we are ensured to have by the Well Ordering Principle.</li> | <li>We note that both of the sets <span class="math-inline"><math>A_1</math></span> and <span class="math-inline"><math>B_1</math></span> cannot be finite since <span class="math-inline"><math>A_1</math></span> and <span class="math-inline"><math>B_1</math></span> contain all of the indices of the sequence <span class="math-inline"><math>(a_n)</math></span> which has infinitely many indices since it is an infinite sequence. If <span class="math-inline"><math>A_1</math></span> is infinite, then we let <span class="math-inline"><math>I_2 = I_1'</math></span>, and we will let <span class="math-inline"><math>n_2</math></span> be the smallest natural number index in the set <span class="math-inline"><math>A_1</math></span>, which we are ensured to have by the Well Ordering Principle. If <span class="math-inline"><math>A_1</math></span> is finite, then <span class="math-inline"><math>B_1</math></span> is infinite and we let <span class="math-inline"><math>I_2 = I_1''</math></span> and we let <span class="math-inline"><math>n_2</math></span> be the smallest natural number index in the set <span class="math-inline"><math>B_1</math></span>, which once again, we are ensured to have by the Well Ordering Principle.</li> | ||
| Line 19: | Line 23: | ||
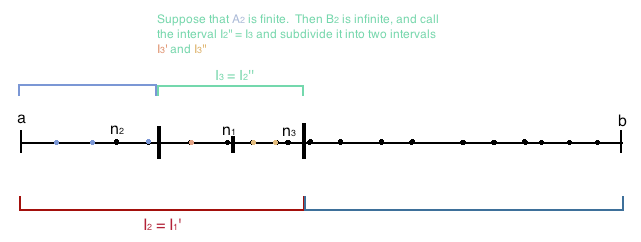
<li>We will now take the interval <span class="math-inline"><math>I_2</math></span> and subdivide it into two subintervals of equal length, call them <span class="math-inline"><math>I_2'</math></span> and <span class="math-inline"><math>I_2''</math></span>. Once again, we will subdivide the set of indices into two sets. Let <span class="math-inline"><math>A_2 = \{ n \in \mathbb{N} : n > n_2, a_n \in I_2' \}</math></span> and let <span class="math-inline"><math>B_2 = \{ n \in \mathbb{N} : n > n_2, a_n \in I_2'' \}</math></span>.</li> | <li>We will now take the interval <span class="math-inline"><math>I_2</math></span> and subdivide it into two subintervals of equal length, call them <span class="math-inline"><math>I_2'</math></span> and <span class="math-inline"><math>I_2''</math></span>. Once again, we will subdivide the set of indices into two sets. Let <span class="math-inline"><math>A_2 = \{ n \in \mathbb{N} : n > n_2, a_n \in I_2' \}</math></span> and let <span class="math-inline"><math>B_2 = \{ n \in \mathbb{N} : n > n_2, a_n \in I_2'' \}</math></span>.</li> | ||
</ul> | </ul> | ||
| − | + | ||
| + | [[File:Bolzano-Weierstrass 3.png|center|Bolzano-Weierstrass 3]] | ||
| + | |||
<ul> | <ul> | ||
<li>Once again, if <span class="math-inline"><math>A_2</math></span> is infinite, then we will let <span class="math-inline"><math>I_3 = I_2'</math></span>, and let <span class="math-inline"><math>n_3</math></span> be the smallest natural number index of <span class="math-inline"><math>A_2</math></span>. If <span class="math-inline"><math>A_2</math></span> is finite, then <span class="math-inline"><math>B_2</math></span> is infinite and let <span class="math-inline"><math>n_3</math></span> be the smallest natural number index of <span class="math-inline"><math>B_2</math></span>.</li> | <li>Once again, if <span class="math-inline"><math>A_2</math></span> is infinite, then we will let <span class="math-inline"><math>I_3 = I_2'</math></span>, and let <span class="math-inline"><math>n_3</math></span> be the smallest natural number index of <span class="math-inline"><math>A_2</math></span>. If <span class="math-inline"><math>A_2</math></span> is finite, then <span class="math-inline"><math>B_2</math></span> is infinite and let <span class="math-inline"><math>n_3</math></span> be the smallest natural number index of <span class="math-inline"><math>B_2</math></span>.</li> | ||
| Line 26: | Line 32: | ||
<li>We will then take the interval <span class="math-inline"><math>I_3</math></span> and subdivide it into two subintervals of equal length, call them <span class="math-inline"><math>I_3'</math></span> and <span class="math-inline"><math>I_3''</math></span>. We will also subdivide the set of indices into two sets. <span class="math-inline"><math>A_3 = \{ n \in \mathbb{N} : n > n_3, a_n \in I_3' \}</math></span> and <span class="math-inline"><math>B_3 = \{ n \in \mathbb{N} : n > n_3, a_n \in I_3'' \}</math></span></li> | <li>We will then take the interval <span class="math-inline"><math>I_3</math></span> and subdivide it into two subintervals of equal length, call them <span class="math-inline"><math>I_3'</math></span> and <span class="math-inline"><math>I_3''</math></span>. We will also subdivide the set of indices into two sets. <span class="math-inline"><math>A_3 = \{ n \in \mathbb{N} : n > n_3, a_n \in I_3' \}</math></span> and <span class="math-inline"><math>B_3 = \{ n \in \mathbb{N} : n > n_3, a_n \in I_3'' \}</math></span></li> | ||
</ul> | </ul> | ||
| − | + | ||
| + | [[File:Bolzano-Weierstrass 4.png|center|Bolzano-Weierstrass 4]] | ||
| + | |||
<ul> | <ul> | ||
<li>We will continue this pattern to obtain a sequence of nested intervals <span class="math-inline"><math>I_1 \supseteq I_2 \supseteq ... \supseteq I_k \supseteq ...</math></span>. Furthermore, we will also have a subsequence <span class="math-inline"><math>(a_{n_k})</math></span> of <span class="math-inline"><math>(a_n)</math></span> where <span class="math-inline"><math>a_{n_k} \in I_k</math></span> for every <span class="math-inline"><math>k \in \mathbb{N}</math></span>.</li> | <li>We will continue this pattern to obtain a sequence of nested intervals <span class="math-inline"><math>I_1 \supseteq I_2 \supseteq ... \supseteq I_k \supseteq ...</math></span>. Furthermore, we will also have a subsequence <span class="math-inline"><math>(a_{n_k})</math></span> of <span class="math-inline"><math>(a_n)</math></span> where <span class="math-inline"><math>a_{n_k} \in I_k</math></span> for every <span class="math-inline"><math>k \in \mathbb{N}</math></span>.</li> | ||
</ul> | </ul> | ||
| − | + | ||
| + | [[File:Bolzano-Weierstrass 5.png|center|Bolzano-Weierstrass 5]] | ||
| + | |||
<ul> | <ul> | ||
<li>We also note that the length of any interval <span class="math-inline"><math>I_k</math></span> is precisely equal to <span class="math-inline"><math>\frac{b - a}{2^{k-1}}</math></span>. By the nested intervals theorem there exists a common point <span class="math-inline"><math>\xi \in I_k</math></span> for all <span class="math-inline"><math>k \in \mathbb{N}</math></span>, and so we have that:</li> | <li>We also note that the length of any interval <span class="math-inline"><math>I_k</math></span> is precisely equal to <span class="math-inline"><math>\frac{b - a}{2^{k-1}}</math></span>. By the nested intervals theorem there exists a common point <span class="math-inline"><math>\xi \in I_k</math></span> for all <span class="math-inline"><math>k \in \mathbb{N}</math></span>, and so we have that:</li> | ||
| Line 53: | Line 63: | ||
<li>But then convergence of <span class="math-inline"><math>A''</math></span> to <span class="math-inline"><math>L</math></span> contradicts the assumption that <span class="math-inline"><math>\mid a_{n_k} - L \mid \geq \epsilon_0</math></span>, and so the assumption that <span class="math-inline"><math>A</math></span> did not converge to <span class="math-inline"><math>L</math></span> was false. Therefore <span class="math-inline"><math>(a_n)</math></span> converges to <span class="math-inline"><math>L</math></span>. <span class="math-inline"><math>\blacksquare</math></span></li> | <li>But then convergence of <span class="math-inline"><math>A''</math></span> to <span class="math-inline"><math>L</math></span> contradicts the assumption that <span class="math-inline"><math>\mid a_{n_k} - L \mid \geq \epsilon_0</math></span>, and so the assumption that <span class="math-inline"><math>A</math></span> did not converge to <span class="math-inline"><math>L</math></span> was false. Therefore <span class="math-inline"><math>(a_n)</math></span> converges to <span class="math-inline"><math>L</math></span>. <span class="math-inline"><math>\blacksquare</math></span></li> | ||
</ul> | </ul> | ||
| + | |||
| + | ==Licensing== | ||
| + | Content obtained and/or adapted from: | ||
| + | * [http://mathonline.wikidot.com/the-bolzano-weierstrass-theorem The Bolzano-Weierstrass Theorem] under a CC BY-SA license | ||
Latest revision as of 12:26, 8 November 2021
Theorem 1 (Bolzano-Weierstrass): Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} be a bounded sequence. Then there exists a subsequence of , call it that is convergent.
- Proof 1: Let be a bounded sequence, that is the set is bounded. Suppose that is a lower bound for this set, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} is an upper bound for this set, and so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a \leq a_n \leq b_n} for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \in \mathbb{N}} . Therefore the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ a_n : n \in \mathbb{N} \}} is contained in the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1 = [a, b]} .
- Let's take Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1 = 1} , i.e., let the first term of the subsequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} be equal to the first term of the parent sequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} .
- We will now take the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1} and divide into two subintervals of equal length. We will call these intervals Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1'} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1''} . We will also divide the set of indices into two sets. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1 := \{ n \in \mathbb{N} : n > n_1, a_n \in I_1' \}} and let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1 = \{ n \in \mathbb{N} : n > n_1, a_N \in I_1'' \}} . We note that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} is the set of indices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} greater than the first index in our subsequence, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1} , such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n} is in the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1'} . Similarly, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1} is the set of indices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} greater than the first index in our subsequence, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1} such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_N} is in the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1''} .
- We note that both of the sets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1} cannot be finite since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1} contain all of the indices of the sequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} which has infinitely many indices since it is an infinite sequence. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} is infinite, then we let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2 = I_1'} , and we will let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2} be the smallest natural number index in the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} , which we are ensured to have by the Well Ordering Principle. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} is finite, then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1} is infinite and we let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2 = I_1''} and we let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2} be the smallest natural number index in the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1} , which once again, we are ensured to have by the Well Ordering Principle.
- We will now take the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2} and subdivide it into two subintervals of equal length, call them Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2'} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2''} . Once again, we will subdivide the set of indices into two sets. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2 = \{ n \in \mathbb{N} : n > n_2, a_n \in I_2' \}} and let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_2 = \{ n \in \mathbb{N} : n > n_2, a_n \in I_2'' \}} .
- Once again, if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2} is infinite, then we will let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_3 = I_2'} , and let be the smallest natural number index of . If is finite, then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_2} is infinite and let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_3} be the smallest natural number index of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_2} .
- We will then take the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_3} and subdivide it into two subintervals of equal length, call them Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_3'} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_3''} . We will also subdivide the set of indices into two sets. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_3 = \{ n \in \mathbb{N} : n > n_3, a_n \in I_3' \}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_3 = \{ n \in \mathbb{N} : n > n_3, a_n \in I_3'' \}}
- We will continue this pattern to obtain a sequence of nested intervals Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1 \supseteq I_2 \supseteq ... \supseteq I_k \supseteq ...} . Furthermore, we will also have a subsequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n_k} \in I_k} for every Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \in \mathbb{N}} .
- We also note that the length of any interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_k} is precisely equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{b - a}{2^{k-1}}} . By the nested intervals theorem there exists a common point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi \in I_k} for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \in \mathbb{N}} , and so we have that:
- Therefore the subsequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} converges to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} . Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \blacksquare}
- Proof 2: Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} be a bounded sequence. By the <a href="/the-monotone-subsequence-theorem">The Monotone Subsequence Theorem</a>, every sequence of real numbers has a monotonic subsequence. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} be this monotonic subsequence. Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} is bounded, it follows that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} is also bounded since the values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n_k}} are contained in the sequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} . Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} is both bounded and monotonic, then by <a href="/the-monotone-convergence-theorem">The Monotone Convergence Theorem</a>, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} is a convergent subsequence. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \blacksquare}
Theorem 2: If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} is a bounded sequence such that every convergent subsequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{n_k})} of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} converges to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} converges to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} .
- Proof: Suppose that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = (a_n)} does not converge to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} . Then there exists a subsequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A' = (a_{n_k})} and an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_0 > 0} such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid a_{n_k} - L \mid \geq \epsilon_0} for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \in \mathbb{N}} .
- Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is bounded, any subsequence of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is also bounded, and so the subsequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'} is bounded. Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'} is bounded, then by the Bolzano-Weierstrass theorem there exists a convergent subsequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A''} of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'} . Since is a convergent subsequence of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'} , then it is also a convergent sequence of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} by transitivity, and by the hypothesis, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A''} converges to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} .
- But then convergence of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A''} to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} contradicts the assumption that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid a_{n_k} - L \mid \geq \epsilon_0} , and so the assumption that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} did not converge to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} was false. Therefore Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_n)} converges to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} . Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \blacksquare}
Licensing
Content obtained and/or adapted from:
- The Bolzano-Weierstrass Theorem under a CC BY-SA license