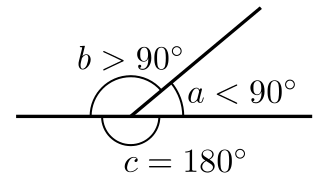Difference between revisions of "Lines & Angles"
(→Units) |
|||
| (19 intermediate revisions by the same user not shown) | |||
| Line 20: | Line 20: | ||
==In Euclidean geometry== | ==In Euclidean geometry== | ||
| − | When geometry was first formalized by Euclid in the ''Elements'', he defined a general line (straight or curved) to be "breadthless length" with a straight line being a line "which lies evenly with the points on itself". | + | When geometry was first formalized by Euclid in the ''Elements'', he defined a general line (straight or curved) to be "breadthless length" with a straight line being a line "which lies evenly with the points on itself". These definitions serve little purpose, since they use terms which are not by themselves defined. In fact, Euclid himself did not use these definitions in this work, and probably included them just to make it clear to the reader what was being discussed. In modern geometry, a line is simply taken as an undefined object with properties given by axioms, but is sometimes defined as a set of points obeying a linear relationship when some other fundamental concept is left undefined. |
In an axiomatic formulation of Euclidean geometry, such as that of Hilbert (Euclid's original axioms contained various flaws which have been corrected by modern mathematicians) a line is stated to have certain properties which relate it to other lines and points. For example, for any two distinct points, there is a unique line containing them, and any two distinct lines intersect in at most one point. In two dimensions (i.e., the Euclidean plane), two lines which do not intersect are called parallel. In higher dimensions, two lines that do not intersect are parallel if they are contained in a plane, or skew if they are not. | In an axiomatic formulation of Euclidean geometry, such as that of Hilbert (Euclid's original axioms contained various flaws which have been corrected by modern mathematicians) a line is stated to have certain properties which relate it to other lines and points. For example, for any two distinct points, there is a unique line containing them, and any two distinct lines intersect in at most one point. In two dimensions (i.e., the Euclidean plane), two lines which do not intersect are called parallel. In higher dimensions, two lines that do not intersect are parallel if they are contained in a plane, or skew if they are not. | ||
| Line 86: | Line 86: | ||
::<math>\frac{c}{|c|}\sqrt{a^2 + b^2}.</math> | ::<math>\frac{c}{|c|}\sqrt{a^2 + b^2}.</math> | ||
| − | Unlike the slope-intercept and intercept forms, this form can represent any line but also requires only two finite parameters, <math>\varphi</math> and {{math|''p''}}, to be specified. If {{math|''p'' > 0}}, then <math>\varphi</math> is uniquely defined modulo | + | Unlike the slope-intercept and intercept forms, this form can represent any line but also requires only two finite parameters, <math>\varphi</math> and {{math|''p''}}, to be specified. If {{math|''p'' > 0}}, then <math>\varphi</math> is uniquely defined modulo <math>2 \pi </math>. On the other hand, if the line is through the origin ({{math|1=''c'' = ''p'' = 0}}), one drops the ''c''/|''c''| term to compute <math>\sin\varphi</math> and <math>\cos\varphi</math>, and it follows that <math>\varphi</math> is only defined modulo <math> \pi </math>. |
===In polar coordinates=== | ===In polar coordinates=== | ||
| Line 184: | Line 184: | ||
[[File:Ray (A, B, C).svg|500px|center|Ray]] | [[File:Ray (A, B, C).svg|500px|center|Ray]] | ||
| − | Thus, we would say that two different points, ''A'' and ''B'', define a line and a decomposition of this line into the disjoint union of an open segment | + | Thus, we would say that two different points, ''A'' and ''B'', define a line and a decomposition of this line into the disjoint union of an open segment (''A'', ''B'') and two rays, ''BC'' and ''AD'' (the point ''D'' is not drawn in the diagram, but is to the left of ''A'' on the line ''AB''). These are not opposite rays since they have different initial points. |
In Euclidean geometry two rays with a common endpoint form an angle. | In Euclidean geometry two rays with a common endpoint form an angle. | ||
| Line 218: | Line 218: | ||
* An angle equal to 0° or not turned is called a zero angle. | * An angle equal to 0° or not turned is called a zero angle. | ||
* An angle smaller than a right angle (less than 90°) is called an ''acute angle'' ("acute" meaning "sharp"). | * An angle smaller than a right angle (less than 90°) is called an ''acute angle'' ("acute" meaning "sharp"). | ||
| − | * An angle equal to <math> \ | + | * An angle equal to <math> \tfrac{1}{4}</math> turn (90° or <math> \tfrac{\pi}{2}</math> radians) is called a ''right angle''. Two lines that form a right angle are said to be ''normal'', ''orthogonal'', or ''perpendicular''. |
* An angle larger than a right angle and smaller than a straight angle (between 90° and 180°) is called an ''obtuse angle'' ("obtuse" meaning "blunt"). | * An angle larger than a right angle and smaller than a straight angle (between 90° and 180°) is called an ''obtuse angle'' ("obtuse" meaning "blunt"). | ||
| − | * An angle equal to <math> \ | + | * An angle equal to <math> \tfrac{1}{2}</math> turn (180° or π radians) is called a ''straight angle''. |
* An angle larger than a straight angle but less than 1 turn (between 180° and 360°) is called a ''reflex angle''. | * An angle larger than a straight angle but less than 1 turn (between 180° and 360°) is called a ''reflex angle''. | ||
* An angle equal to 1 turn (360° or 2π radians) is called a ''full angle'', ''complete angle'', ''round angle'' or a ''perigon''. | * An angle equal to 1 turn (360° or 2π radians) is called a ''full angle'', ''complete angle'', ''round angle'' or a ''perigon''. | ||
| Line 247: | Line 247: | ||
|style = "background:#f2f2f2; text-align:center;" | turn | |style = "background:#f2f2f2; text-align:center;" | turn | ||
| 0 turn | | 0 turn | ||
| − | | <math> \left (0, \ | + | | <math> \left (0, \tfrac{1}{4} \right ) </math> turn |
| − | | <math> \ | + | | <math> \tfrac{1}{4} </math> turn |
| − | | <math> \left ( \ | + | | <math> \left ( \tfrac{1}{4}, \tfrac{1}{2} \right ) </math> turn |
| − | | <math> \ | + | | <math> \tfrac{1}{2} </math> turn |
| − | | <math> \left ( \ | + | | <math> \left ( \tfrac{1}{2}, 1 \right )</math> turn |
| 1 turn | | 1 turn | ||
|- | |- | ||
|style = "background:#f2f2f2; text-align:center;" | radian | |style = "background:#f2f2f2; text-align:center;" | radian | ||
| 0 rad | | 0 rad | ||
| − | | <math> \left (0, \ | + | | <math> \left (0, \tfrac{1}{2} \pi \right ) </math> rad |
| − | | <math> \ | + | | <math> \tfrac{1}{2} \pi </math> rad |
| − | | <math> \left ( \ | + | | <math> \left ( \tfrac{1}{2} \pi, \pi \right ) </math> rad |
| <math> \pi </math> rad | | <math> \pi </math> rad | ||
| (<math> \pi </math>, <math> 2 \pi </math>) rad | | (<math> \pi </math>, <math> 2 \pi </math>) rad | ||
| Line 286: | Line 286: | ||
* Angles that have the same measure (i.e. the same magnitude) are said to be ''equal'' or ''congruent''. An angle is defined by its measure and is not dependent upon the lengths of the sides of the angle (e.g. all ''right angles'' are equal in measure). | * Angles that have the same measure (i.e. the same magnitude) are said to be ''equal'' or ''congruent''. An angle is defined by its measure and is not dependent upon the lengths of the sides of the angle (e.g. all ''right angles'' are equal in measure). | ||
* Two angles that share terminal sides, but differ in size by an integer multiple of a turn, are called ''coterminal angles''. | * Two angles that share terminal sides, but differ in size by an integer multiple of a turn, are called ''coterminal angles''. | ||
| − | * A ''reference angle'' is the acute version of any angle determined by repeatedly subtracting or adding straight angle (<math> \ | + | * A ''reference angle'' is the acute version of any angle determined by repeatedly subtracting or adding straight angle (<math> \tfrac{1}{2}</math> turn, 180°, or π radians), to the results as necessary, until the magnitude of the result is an acute angle, a value between 0 and <math> \tfrac{1}{4}</math> turn, 90°, or <math> \tfrac {\pi}{2}</math> radians. For example, an angle of 30 degrees has a reference angle of 30 degrees, and an angle of 150 degrees also has a reference angle of 30 degrees (180–150). An angle of 750 degrees has a reference angle of 30 degrees (750–720). |
=== Vertical and adjacent angle pairs=== | === Vertical and adjacent angle pairs=== | ||
| Line 308: | Line 308: | ||
Three special angle pairs involve the summation of angles: | Three special angle pairs involve the summation of angles: | ||
[[File:Complement angle.svg|thumb|150px|The ''complementary'' angles <var>a</var> and <var>b</var> (<var>b</var> is the ''complement'' of <var>a</var>, and <var>a</var> is the complement of <var>b</var>).]] | [[File:Complement angle.svg|thumb|150px|The ''complementary'' angles <var>a</var> and <var>b</var> (<var>b</var> is the ''complement'' of <var>a</var>, and <var>a</var> is the complement of <var>b</var>).]] | ||
| − | * ''Complementary angles'' are angle pairs whose measures sum to one right angle ({{ | + | * ''Complementary angles'' are angle pairs whose measures sum to one right angle (<math> \tfrac{1}{4}</math> turn, 90°, or <math> \tfrac{\pi}{2}</math> radians). If the two complementary angles are adjacent, their non-shared sides form a right angle. In Euclidean geometry, the two acute angles in a right triangle are complementary, because the sum of internal angles of a triangle is 180 degrees, and the right angle itself accounts for 90 degrees. |
:The adjective complementary is from Latin ''complementum'', associated with the verb ''complere'', "to fill up". An acute angle is "filled up" by its complement to form a right angle. | :The adjective complementary is from Latin ''complementum'', associated with the verb ''complere'', "to fill up". An acute angle is "filled up" by its complement to form a right angle. | ||
:The difference between an angle and a right angle is termed the ''complement'' of the angle. | :The difference between an angle and a right angle is termed the ''complement'' of the angle. | ||
| Line 320: | Line 320: | ||
:(The tangent of an angle equals the cotangent of its complement and its secant equals the cosecant of its complement.) | :(The tangent of an angle equals the cotangent of its complement and its secant equals the cosecant of its complement.) | ||
:The prefix "co-" in the names of some trigonometric ratios refers to the word "complementary". | :The prefix "co-" in the names of some trigonometric ratios refers to the word "complementary". | ||
| − | + | ||
[[File:Angle obtuse acute straight.svg|thumb|right|300px|The angles <var>a</var> and <var>b</var> are ''supplementary'' angles.]] | [[File:Angle obtuse acute straight.svg|thumb|right|300px|The angles <var>a</var> and <var>b</var> are ''supplementary'' angles.]] | ||
| − | * Two angles that sum to a straight angle ({{ | + | * Two angles that sum to a straight angle (<math> \tfrac{1}{2}</math> turn, 180°, or π radians) are called ''supplementary angles''. |
| − | :If the two supplementary angles are adjacent (i.e. have a common vertex and share just one side), their non-shared sides form a straight line. Such angles are called a ''linear pair of angles''. However, supplementary angles do not have to be on the same line, and can be separated in space. For example, adjacent angles of a | + | :If the two supplementary angles are adjacent (i.e. have a common vertex and share just one side), their non-shared sides form a straight line. Such angles are called a ''linear pair of angles''. However, supplementary angles do not have to be on the same line, and can be separated in space. For example, adjacent angles of a parallelogram are supplementary, and opposite angles of a cyclic quadrilateral (one whose vertices all fall on a single circle) are supplementary. |
:If a point P is exterior to a circle with center O, and if the tangent lines from P touch the circle at points T and Q, then ∠TPQ and ∠TOQ are supplementary. | :If a point P is exterior to a circle with center O, and if the tangent lines from P touch the circle at points T and Q, then ∠TPQ and ∠TOQ are supplementary. | ||
:The sines of supplementary angles are equal. Their cosines and tangents (unless undefined) are equal in magnitude but have opposite signs. | :The sines of supplementary angles are equal. Their cosines and tangents (unless undefined) are equal in magnitude but have opposite signs. | ||
:In Euclidean geometry, any sum of two angles in a triangle is supplementary to the third, because the sum of internal angles of a triangle is a straight angle. | :In Euclidean geometry, any sum of two angles in a triangle is supplementary to the third, because the sum of internal angles of a triangle is a straight angle. | ||
| − | + | ||
[[File:Reflex angle.svg|thumb|right|150px|Sum of two ''explementary'' angles is a ''complete'' angle.]] | [[File:Reflex angle.svg|thumb|right|150px|Sum of two ''explementary'' angles is a ''complete'' angle.]] | ||
| − | * Two angles that sum to a complete angle (1 turn, 360°, or | + | * Two angles that sum to a complete angle (1 turn, 360°, or 2π radians) are called ''explementary angles'' or ''conjugate angles''. |
*: The difference between an angle and a complete angle is termed the ''explement'' of the angle or ''conjugate'' of an angle. | *: The difference between an angle and a complete angle is termed the ''explement'' of the angle or ''conjugate'' of an angle. | ||
| − | |||
===Polygon-related angles=== | ===Polygon-related angles=== | ||
[[File:ExternalAngles.svg|thumb|300px|right|Internal and external angles.]] | [[File:ExternalAngles.svg|thumb|300px|right|Internal and external angles.]] | ||
* An angle that is part of a simple polygon is called an ''interior angle'' if it lies on the inside of that simple polygon. A simple concave polygon has at least one interior angle that is a reflex angle. | * An angle that is part of a simple polygon is called an ''interior angle'' if it lies on the inside of that simple polygon. A simple concave polygon has at least one interior angle that is a reflex angle. | ||
| − | *: In Euclidean geometry, the measures of the interior angles of a triangle add up to | + | *: In Euclidean geometry, the measures of the interior angles of a triangle add up to π radians, 180°, or <math> \tfrac{1}{2}</math> turn; the measures of the interior angles of a simple convex quadrilateral add up to 2{{math|π}} radians, 360°, or 1 turn. In general, the measures of the interior angles of a simple convex polygon with ''n'' sides add up to (''n'' − 2){{math|π}} radians, or (''n'' − 2)180 degrees, (''n'' − 2)2 right angles, or (''n'' − 2)<math> \tfrac{1}{2}</math> turn. |
* The supplement of an interior angle is called an ''exterior angle'', that is, an interior angle and an exterior angle form a linear pair of angles. There are two exterior angles at each vertex of the polygon, each determined by extending one of the two sides of the polygon that meet at the vertex; these two angles are vertical and hence are equal. An exterior angle measures the amount of rotation one has to make at a vertex to trace out the polygon. If the corresponding interior angle is a reflex angle, the exterior angle should be considered negative. Even in a non-simple polygon it may be possible to define the exterior angle, but one will have to pick an orientation of the plane (or surface) to decide the sign of the exterior angle measure. | * The supplement of an interior angle is called an ''exterior angle'', that is, an interior angle and an exterior angle form a linear pair of angles. There are two exterior angles at each vertex of the polygon, each determined by extending one of the two sides of the polygon that meet at the vertex; these two angles are vertical and hence are equal. An exterior angle measures the amount of rotation one has to make at a vertex to trace out the polygon. If the corresponding interior angle is a reflex angle, the exterior angle should be considered negative. Even in a non-simple polygon it may be possible to define the exterior angle, but one will have to pick an orientation of the plane (or surface) to decide the sign of the exterior angle measure. | ||
*: In Euclidean geometry, the sum of the exterior angles of a simple convex polygon, if only one of the two exterior angles is assumed at each vertex, will be one full turn (360°). The exterior angle here could be called a ''supplementary exterior angle''. Exterior angles are commonly used in Logo Turtle programs when drawing regular polygons. | *: In Euclidean geometry, the sum of the exterior angles of a simple convex polygon, if only one of the two exterior angles is assumed at each vertex, will be one full turn (360°). The exterior angle here could be called a ''supplementary exterior angle''. Exterior angles are commonly used in Logo Turtle programs when drawing regular polygons. | ||
| Line 353: | Line 352: | ||
In some contexts, such as identifying a point on a circle or describing the ''orientation'' of an object in two dimensions relative to a reference orientation, angles that differ by an exact multiple of a full turn are effectively equivalent. In other contexts, such as identifying a point on a spiral curve or describing the ''cumulative rotation'' of an object in two dimensions relative to a reference orientation, angles that differ by a non-zero multiple of a full turn are not equivalent. | In some contexts, such as identifying a point on a circle or describing the ''orientation'' of an object in two dimensions relative to a reference orientation, angles that differ by an exact multiple of a full turn are effectively equivalent. In other contexts, such as identifying a point on a spiral curve or describing the ''cumulative rotation'' of an object in two dimensions relative to a reference orientation, angles that differ by a non-zero multiple of a full turn are not equivalent. | ||
| − | [[File:Angle measure.svg|right|thumb|The measure of angle {{math|''θ''}} is {{ | + | [[File:Angle measure.svg|right|thumb|The measure of angle {{math|''θ''}} is <math> \frac{s}{r}</math> radians.]] |
| − | In order to measure an angle <var>θ</var>, a circular arc centered at the vertex of the angle is drawn, e.g. with a pair of compasses. The ratio of the length <var>s</var> of the arc by the radius <var>r</var> of the circle is the number of | + | In order to measure an angle <var>θ</var>, a circular arc centered at the vertex of the angle is drawn, e.g. with a pair of compasses. The ratio of the length <var>s</var> of the arc by the radius <var>r</var> of the circle is the number of radians in the angle. Conventionally, in mathematics and in the SI, the radian is treated as being equal to the dimensionless value 1. |
| − | The angle expressed another angular unit may then be obtained by multiplying the angle by a suitable conversion constant of the form {{ | + | The angle expressed another angular unit may then be obtained by multiplying the angle by a suitable conversion constant of the form <math> \frac{k}{2 \pi} </math>, where ''k'' is the measure of a complete turn expressed in the chosen unit (for example, ''k'' = 360° for degrees or 400 grad for gradians): |
:<math> \theta = \frac{k}{2\pi} \cdot \frac{s}{r}. </math> | :<math> \theta = \frac{k}{2\pi} \cdot \frac{s}{r}. </math> | ||
| Line 375: | Line 374: | ||
[[Image:Angle radian.svg|right|thumb|150 px|Definition of 1 radian]] | [[Image:Angle radian.svg|right|thumb|150 px|Definition of 1 radian]] | ||
| − | Throughout history, angles have been | + | Throughout history, angles have been measured in many different units. These are known as '''angular units''', with the most contemporary units being the degree ( ° ), the radian (rad), and the gradian (grad), though many others have been used throughout history. |
| − | Angles expressed in radians are dimensionless for | + | Angles expressed in radians are dimensionless for dimensional analysis. |
| − | Most units of angular measurement are defined such that one | + | Most units of angular measurement are defined such that one turn (i.e. one full circle) is equal to ''n'' units, for some whole number ''n''. The two exceptions are the radian (and its decimal submultiples) and the diameter part. |
| − | One '' | + | One ''radian'' is the angle subtended by an arc of a circle that has the same length as the circle's radius. The radian is the derived quantity of angular measurement in the SI system. By definition, it is dimensionless, though it may be specified as ''rad'' to avoid ambiguity. Angles measured in degrees, are shown with the symbol °. Subdivisions of the degree are minute (symbol ′, 1′ = 1/60°) and second {symbol ″, 1″ = 1/3600°}. An angle of 360° corresponds to the angle subtended by a full circle, and is equal to 2''π'' radians, or 400 gradians. |
| − | Other units used to represent angles are listed in the following table. These units are defined such that the number of | + | Other units used to represent angles are listed in the following table. These units are defined such that the number of turns is equivalent to a full circle. |
{|class = "wikitable" | {|class = "wikitable" | ||
!name !!number in one turn!!rotation angle !!description | !name !!number in one turn!!rotation angle !!description | ||
|- | |- | ||
| − | + | |Turn||1||360° || The ''turn'', also ''cycle'', ''full circle'', ''revolution'', and ''rotation'', is complete circular movement or measure (as to return to the same point) with circle or ellipse. A turn is abbreviated {{mvar|τ}}, ''cyc'', ''rev'', or ''rot'' depending on the application.. The symbol {{mvar|τ}} can also be used as a mathematical constant to represent 2π radians. | |
|- | |- | ||
| − | | | + | |Multiples of <math> \pi </math> ||2||180° || The ''multiples of <math> \pi </math>'' (MUL<math> \pi </math>) unit is implemented in the RPN scientific calculator WP 43S. See also: IEEE 754 recommended operations |
|- | |- | ||
| − | + | |Quadrant||4||90°||One ''quadrant'' is a <math> \tfrac{1}{4}</math> turn and also known as a ''right angle''. The quadrant is the unit used in Euclid's Elements. In German the symbol <sup>∟</sup> has been used to denote a quadrant. It is the unit used in Euclid's Elements. 1 quad = 90° = <math> \tfrac{\pi}{2}</math> rad = <math> \tfrac{1}{4}</math> turn = 100 grad. | |
|- | |- | ||
| − | + | |Sextant||6||60°||The ''sextant'' was the unit used by the Babylonians, The degree, minute of arc and second of arc are sexagesimal subunits of the Babylonian unit. It is especially easy to construct with ruler and compasses. It is the ''angle of the equilateral triangle'' or is <math> \tfrac{1}{6}</math> turn. 1 Babylonian unit = 60° = <math> \tfrac{\pi}{3}</math> rad ≈ 1.047197551 rad. | |
|- | |- | ||
| − | | | + | |Radian||{{math|2''π''}}||57°17′||The ''radian'' is determined by the circumference of a circle that is equal in length to the radius of the circle (''n'' = 2π = 6.283...). It is the angle subtended by an arc of a circle that has the same length as the circle's radius. The symbol for radian is ''rad''. One turn is 2{{math|π}} radians, and one radian is <math> \tfrac{180^ \circ}{\pi}</math>, or about 57.2958 degrees. In mathematical texts, angles are often treated as being dimensionless with the radian equal to one, resulting in the unit ''rad'' often being omitted. The radian is used in virtually all mathematical work beyond simple practical geometry, due, for example, to the pleasing and "natural" properties that the trigonometric functions display when their arguments are in radians. The radian is the (derived) unit of angular measurement in the SI, which also treats angle as being dimensionless. |
|- | |- | ||
| − | | Hexacontade||60 ||6°||The ''hexacontade'' is a unit used by | + | | Hexacontade||60 ||6°||The ''hexacontade'' is a unit used by Eratosthenes. It is equal to 6°, so that a whole turn was divided into 60 hexacontades. |
|- | |- | ||
| − | + | |Binary degree ||256||1°33'45" || The ''binary degree'', also known as the ''binary radian'' (or ''brad''). The binary degree is used in computing so that an angle can be efficiently represented in a single byte (albeit to limited precision). Other measures of angle used in computing may be based on dividing one whole turn into 2<sup>''n''</sup> equal parts for other values of ''n''. It is <math> \tfrac{1}{256}</math> of a turn. | |
|- | |- | ||
| − | + | |Degree ||360 ||1°|| One advantage of this old sexagesimal subunit is that many angles common in simple geometry are measured as a whole number of degrees. Fractions of a degree may be written in normal decimal notation (e.g. 3.5° for three and a half degrees), but the "minute" and "second" sexagesimal subunits of the "degree-minute-second" system are also in use, especially for geographical coordinates and in astronomy and ballistics (''n'' = 360) The ''degree'', denoted by a small superscript circle (°), is 1/360 of a turn, so one ''turn'' is 360°. The case of degrees for the formula given earlier, a ''degree'' of ''n'' = 360° units is obtained by setting ''k'' = <math> \tfrac{360^ \circ}{2 \pi}</math>. | |
|- | |- | ||
| − | + | | Grad||400 ||0°54′ || The ''grad'', also called ''grade'', ''gradian'', or ''gon''. a right angle is 100 grads. It is a decimal subunit of the quadrant. A kilometre was historically defined as a centi-grad of arc along a meridian of the Earth, so the kilometer is the decimal analog to the sexagesimal nautical mile (''n'' = 400). The grad is used mostly in triangulation and continental surveying. | |
|- | |- | ||
| − | | | + | | Minute of arc||21,600 ||0°1′|| The ''minute of arc'' (or ''MOA'', ''arcminute'', or just ''minute'') is <math> \tfrac{1}{60} </math> of a degree. A nautical mile was historically defined as a minute of arc along a great circle of the Earth (''n'' = 21,600). The ''arcminute'' is <math> \tfrac{1}{60} </math> of a degree = <math> \tfrac{1}{21,600} </math> turn. It is denoted by a single prime ( ′ ). For example, 3° 30′ is equal to 3 × 60 + 30 = 210 minutes or 3 + <math> \tfrac{30}{60} </math> = 3.5 degrees. A mixed format with decimal fractions is also sometimes used, e.g. 3° 5.72′ = 3 + <math> \tfrac{5.72}{60} </math> degrees. A nautical mile was historically defined as an arcminute along a great circle of the Earth. |
|- | |- | ||
| − | | | + | | Second of arc||1,296,000 ||0°0′1″||The ''second of arc'' (or ''arcsecond'', or just ''second'') is <math> \tfrac{1}{60} </math> of a minute of arc and <math> \tfrac{1}{3600} </math> of a degree (''n'' = 1,296,000). The ''arcsecond'' (or ''second of arc'', or just ''second'') is <math> \tfrac{1}{60} </math> of an arcminute and <math> \tfrac{1}{3600} </math> of a degree. It is denoted by a double prime ( ″ ). For example, 3° 7′ 30″ is equal to 3 + <math> \tfrac{7}{60} </math> + <math> \tfrac{30}{3600} </math> degrees, or 3.125 degrees. |
|} | |} | ||
===Other descriptors=== | ===Other descriptors=== | ||
| − | * | + | * Hour angle (''n'' = 24): The astronomical ''hour angle'' is <math> \tfrac{1}{24} </math> turn. As this system is amenable to measuring objects that cycle once per day (such as the relative position of stars), the sexagesimal subunits are called ''minute of time'' and ''second of time''. These are distinct from, and 15 times larger than, minutes and seconds of arc. 1 hour = 15° = <math> \tfrac{\pi}{12} </math> rad = <math> \tfrac{1}{6} </math> quad = <math> \tfrac{1}{24} </math>turn = <math> 16 \tfrac{2}{3} </math> grad. |
| − | * | + | |
| − | * | + | * (Compass) point or wind (''n'' = 32): The ''point'', used in navigation, is <math> \tfrac{1}{32} </math> of a turn. 1 point = <math> \tfrac{1}{8} </math> of a right angle = 11.25° = 12.5 grad. Each point is subdivided in four quarter-points so that 1 turn equals 128 quarter-points. |
| − | * | + | |
| − | * Chi, an old Chinese angle measurement. | + | * Pechus (''n'' = 144–180): The ''pechus'' was a Babylonian unit equal to about 2° or <math> {2 \tfrac{1}{2}} ^ \circ </math>. |
| − | * Diameter part (''n'' = 376.99...): The ''diameter part'' (occasionally used in Islamic mathematics) is {{ | + | |
| − | * | + | * Tau, the number of radians in one turn (1 turn = {{mvar|τ}} rad), ''τ'' = 2''π''. |
| − | * Akhnam and zam. In old Arabia a | + | |
| + | * Chi, an old Chinese angle measurement. | ||
| + | |||
| + | * Diameter part (''n'' = 376.99...): The ''diameter part'' (occasionally used in Islamic mathematics) is <math> \tfrac{1}{60} </math> radian. One "diameter part" is approximately 0.95493°. There are about 376.991 diameter parts per turn. | ||
| + | |||
| + | * Milliradian and derived definitions: The true milliradian is defined a thousandth of a radian, which means that a rotation of one turn would equal exactly 2000π mil (or approximately 6283.185 mil), and almost all scope sights for firearms are calibrated to this definition. In addition there are three other derived definitions used for artillery and navigation which are ''approximately'' equal to a milliradian. Under these three other definitions one turn makes up for exactly 6000, 6300 or 6400 mils, which equals spanning the range from 0.05625 to 0.06 degrees (3.375 to 3.6 minutes). In comparison, the true milliradian is approximately 0.05729578 degrees (3.43775 minutes). One "NATO mil" is defined as <math> \tfrac{1}{6400} </math> of a circle. Just like with the true milliradian, each of the other definitions exploits the mil's useful property of subtensions, i.e. that the value of one milliradian approximately equals the angle subtended by a width of 1 meter as seen from 1 km away <math> \left ( \tfrac{2 \pi}{6400} = 0.0009817 \ldots \approx \tfrac{1}{1000} \right ) </math>. | ||
| + | |||
| + | * Akhnam and zam. In old Arabia a turn was subdivided in 32 Akhnam and each akhnam was subdivided in 7 zam, so that a turn is 224 zam. | ||
===Signed angles=== | ===Signed angles=== | ||
| − | Although the definition of the measurement of an angle does not support the concept of a negative angle, it is frequently useful to impose a convention that allows positive and negative angular values to represent | + | Although the definition of the measurement of an angle does not support the concept of a negative angle, it is frequently useful to impose a convention that allows positive and negative angular values to represent orientations and/or rotations in opposite directions relative to some reference. |
| − | In a two-dimensional | + | In a two-dimensional Cartesian coordinate system, an angle is typically defined by its two sides, with its vertex at the origin. The ''initial side'' is on the positive x-axis, while the other side or ''terminal side'' is defined by the measure from the initial side in radians, degrees, or turns. With ''positive angles'' representing rotations toward the positive y-axis and ''negative angles'' representing rotations toward the negative ''y''-axis. When Cartesian coordinates are represented by ''standard position'', defined by the ''x''-axis rightward and the ''y''-axis upward, positive rotations are anticlockwise and negative rotations are clockwise. |
In many contexts, an angle of −''θ'' is effectively equivalent to an angle of "one full turn minus ''θ''". For example, an orientation represented as −45° is effectively equivalent to an orientation represented as 360° − 45° or 315°. Although the final position is the same, a physical rotation (movement) of −45° is not the same as a rotation of 315° (for example, the rotation of a person holding a broom resting on a dusty floor would leave visually different traces of swept regions on the floor). | In many contexts, an angle of −''θ'' is effectively equivalent to an angle of "one full turn minus ''θ''". For example, an orientation represented as −45° is effectively equivalent to an orientation represented as 360° − 45° or 315°. Although the final position is the same, a physical rotation (movement) of −45° is not the same as a rotation of 315° (for example, the rotation of a person holding a broom resting on a dusty floor would leave visually different traces of swept regions on the floor). | ||
| − | In three-dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined relative to some reference, which is typically a | + | In three-dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined relative to some reference, which is typically a vector passing through the angle's vertex and perpendicular to the plane in which the rays of the angle lie. |
| − | In | + | In navigation, bearings or azimuth are measured relative to north. By convention, viewed from above, bearing angles are positive clockwise, so a bearing of 45° corresponds to a north-east orientation. Negative bearings are not used in navigation, so a north-west orientation corresponds to a bearing of 315°. |
===Alternative ways of measuring the size of an angle=== | ===Alternative ways of measuring the size of an angle=== | ||
There are several alternatives to measuring the size of an angle by the angle of rotation. | There are several alternatives to measuring the size of an angle by the angle of rotation. | ||
| − | The '' | + | The ''slope'' or ''gradient'' is equal to the tangent of the angle, or sometimes (rarely) the sine; a gradient is often expressed as a percentage. For very small values (less than 5%), the grade of a slope is approximately the measure of the angle in radians. |
| − | In | + | In rational geometry the ''spread'' between two lines is defined as the square of the sine of the angle between the lines. As the sine of an angle and the sine of its supplementary angle are the same, any angle of rotation that maps one of the lines into the other leads to the same value for the spread between the lines. |
===Astronomical approximations=== | ===Astronomical approximations=== | ||
| Line 445: | Line 451: | ||
* 20° is approximately the width of a handspan at arm's length. | * 20° is approximately the width of a handspan at arm's length. | ||
| − | These measurements clearly depend on the individual subject, and the above should be treated as rough | + | These measurements clearly depend on the individual subject, and the above should be treated as rough rule of thumb approximations only. |
| − | In | + | In astronomy, right ascension and declination are usually measured in angular units, expressed in terms of time, based on a 24-hour day. |
{|class="wikitable" | {|class="wikitable" | ||
|- | |- | ||
| − | ! Unit !! | + | ! Unit !! Symbol !!Degree !! Radians!! Circle!!Other |
|- | |- | ||
! Hour | ! Hour | ||
| − | | h || 15°|| { | + | | h || 15°|| <math> \tfrac {\pi}{12} </math> ||<math> \tfrac{1}{24} </math>|| |
|- | |- | ||
! Minute | ! Minute | ||
| − | | m || 0°15'||{ | + | | m || 0°15'||<math> \tfrac {\pi}{720} </math>||<math> \tfrac {1}{1,440} </math>||<math> \tfrac {1}{60} </math> hour |
|- | |- | ||
! Second | ! Second | ||
| − | | s|| 0°0'15"|| { | + | | s|| 0°0'15"|| <math> \tfrac {\pi}{43,200} </math> || <math> \tfrac {1}{86,400} </math> || <math> \tfrac {1}{60} </math> minute |
|} | |} | ||
===Measurements that are not angular units=== | ===Measurements that are not angular units=== | ||
| − | Not all angle measurements are angular units, for an angular measurement, it is definitional that the | + | Not all angle measurements are angular units, for an angular measurement, it is definitional that the angle addition postulate holds. |
| − | Some angle measurements where the | + | Some angle measurements where the angle addition postulate does not hold include: |
| − | * | + | * Trigonometric functions |
| − | * | + | * Slope |
==Angles between curves== | ==Angles between curves== | ||
[[File:Curve angles.svg|thumb|right|The angle between the two curves at ''P'' is defined as the angle between the tangents <var>A</var> and <var>B</var> at <var>P</var>.]] | [[File:Curve angles.svg|thumb|right|The angle between the two curves at ''P'' is defined as the angle between the tangents <var>A</var> and <var>B</var> at <var>P</var>.]] | ||
| − | The angle between a line and a | + | The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection. Various names (now rarely, if ever, used) have been given to particular cases:—''amphicyrtic'' (Gr. ἀμφί, on both sides, κυρτός, convex) or ''cissoidal'' (Gr. κισσός, ivy), biconvex; ''xystroidal'' or ''sistroidal'' (Gr. ξυστρίς, a tool for scraping), concavo-convex; ''amphicoelic'' (Gr. κοίλη, a hollow) or ''angulus lunularis'', biconcave. |
==Bisecting and trisecting angles== | ==Bisecting and trisecting angles== | ||
| − | The | + | The ancient Greek mathematicians knew how to bisect an angle (divide it into two angles of equal measure) using only a compass and straightedge, but could only trisect certain angles. In 1837 Pierre Wantzel showed that for most angles this construction cannot be performed. |
==Dot product and generalisations== | ==Dot product and generalisations== | ||
| − | In the | + | In the Euclidean space, the angle ''θ'' between two Euclidean vectors '''u''' and '''v''' is related to their dot product and their lengths by the formula |
:<math> \mathbf{u} \cdot \mathbf{v} = \cos(\theta) \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .</math> | :<math> \mathbf{u} \cdot \mathbf{v} = \cos(\theta) \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .</math> | ||
| − | This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their | + | This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their normal vectors and between skew lines from their vector equations. |
===Inner product=== | ===Inner product=== | ||
| − | To define angles in an abstract real | + | To define angles in an abstract real inner product space, we replace the Euclidean dot product ( '''·''' ) by the inner product <math> \langle \cdot , \cdot \rangle </math>, i.e. |
:<math> \langle \mathbf{u} , \mathbf{v} \rangle = \cos(\theta)\ \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .</math> | :<math> \langle \mathbf{u} , \mathbf{v} \rangle = \cos(\theta)\ \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .</math> | ||
| − | In a complex | + | In a complex inner product space, the expression for the cosine above may give non-real values, so it is replaced with |
:<math> \operatorname{Re} \left( \langle \mathbf{u} , \mathbf{v} \rangle \right) = \cos(\theta) \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .</math> | :<math> \operatorname{Re} \left( \langle \mathbf{u} , \mathbf{v} \rangle \right) = \cos(\theta) \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .</math> | ||
| Line 505: | Line 511: | ||
:<math> \left| \langle \mathbf{u} , \mathbf{v} \rangle \right| = \left| \cos(\theta) \right| \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| </math> | :<math> \left| \langle \mathbf{u} , \mathbf{v} \rangle \right| = \left| \cos(\theta) \right| \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| </math> | ||
| − | in a | + | in a Hilbert space can be extended to subspaces of any finite dimensions. Given two subspaces <math> \mathcal{U} </math>, <math> \mathcal{W} </math> with <math> \dim ( \mathcal{U}) := k \leq \dim ( \mathcal{W}) := l </math>, this leads to a definition of <math>k</math> angles called canonical or principal angles between subspaces. |
===Angles in Riemannian geometry=== | ===Angles in Riemannian geometry=== | ||
| − | In | + | In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where ''U'' and ''V'' are tangent vectors and ''g''<sub>''ij''</sub> are the components of the metric tensor ''G'', |
:<math> | :<math> | ||
| Line 515: | Line 521: | ||
===Hyperbolic angle=== | ===Hyperbolic angle=== | ||
| − | A | + | A hyperbolic angle is an argument of a hyperbolic function just as the ''circular angle'' is the argument of a circular function. The comparison can be visualized as the size of the openings of a hyperbolic sector and a circular sector since the areas of these sectors correspond to the angle magnitudes in each case. Unlike the circular angle, the hyperbolic angle is unbounded. When the circular and hyperbolic functions are viewed as infinite series in their angle argument, the circular ones are just alternating series forms of the hyperbolic functions. This weaving of the two types of angle and function was explained by Leonhard Euler in ''Introduction to the Analysis of the Infinite''. |
==Angles in geography and astronomy== | ==Angles in geography and astronomy== | ||
| − | In | + | In geography, the location of any point on the Earth can be identified using a ''geographic coordinate system''. This system specifies the latitude and longitude of any location in terms of angles subtended at the center of the Earth, using the equator and (usually) the Greenwich meridian as references. |
| − | In | + | In astronomy, a given point on the celestial sphere (that is, the apparent position of an astronomical object) can be identified using any of several ''astronomical coordinate systems'', where the references vary according to the particular system. Astronomers measure the ''angular separation'' of two stars by imagining two lines through the center of the Earth, each intersecting one of the stars. The angle between those lines can be measured and is the angular separation between the two stars. |
| − | In both geography and astronomy, a sighting direction can be specified in terms of a | + | In both geography and astronomy, a sighting direction can be specified in terms of a vertical angle such as altitude /elevation with respect to the horizon as well as the azimuth with respect to north. |
| − | Astronomers also measure the ''apparent size'' of objects as an | + | Astronomers also measure the ''apparent size'' of objects as an angular diameter. For example, the full moon has an angular diameter of approximately 0.5°, when viewed from Earth. One could say, "The Moon's diameter subtends an angle of half a degree." The small-angle formula can be used to convert such an angular measurement into a distance/size ratio. |
| − | + | = Licensing = | |
Content obtained and/or adapted from: | Content obtained and/or adapted from: | ||
* [https://en.wikipedia.org/wiki/Line_(geometry) Line (geometry), Wikipedia] under a CC BY-SA license | * [https://en.wikipedia.org/wiki/Line_(geometry) Line (geometry), Wikipedia] under a CC BY-SA license | ||
* [https://en.wikipedia.org/wiki/Angle Angle, Wikipedia] under a CC BY-SA license | * [https://en.wikipedia.org/wiki/Angle Angle, Wikipedia] under a CC BY-SA license | ||
Latest revision as of 18:13, 12 December 2021
Contents
- 1 Lines
- 2 Angle
- 3 Licensing
Lines
In geometry, the notion of line or straight line was introduced by ancient mathematicians to represent straight objects (i.e., having no curvature) with negligible width and depth. Lines are an idealization of such objects, which are often described in terms of two points (e.g., ) or referred to using a single letter (e.g., ).
Until the 17th century, lines were defined as the "[...] first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which [...] will leave from its imaginary moving some vestige in length, exempt of any width. [...] The straight line is that which is equally extended between its points."
Euclid described a line as "breadthless length" which "lies equally with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as non-Euclidean, projective and affine geometry).
In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation, but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.
When a geometry is described by a set of axioms, the notion of a line is usually left undefined (a so-called primitive object). The properties of lines are then determined by the axioms which refer to them. One advantage to this approach is the flexibility it gives to users of the geometry. Thus in differential geometry, a line may be interpreted as a geodesic (shortest path between points), while in some projective geometries, a line is a 2-dimensional vector space (all linear combinations of two independent vectors). This flexibility also extends beyond mathematics and, for example, permits physicists to think of the path of a light ray as being a line.
Definitions versus descriptions
All definitions are ultimately circular in nature, since they depend on concepts which must themselves have definitions, a dependence which cannot be continued indefinitely without returning to the starting point. To avoid this vicious circle, certain concepts must be taken as primitive concepts; terms which are given no definition. In geometry, it is frequently the case that the concept of line is taken as a primitive. In those situations where a line is a defined concept, as in coordinate geometry, some other fundamental ideas are taken as primitives. When the line concept is a primitive, the behaviour and properties of lines are dictated by the axioms which they must satisfy.
In a non-axiomatic or simplified axiomatic treatment of geometry, the concept of a primitive notion may be too abstract to be dealt with. In this circumstance, it is possible to provide a description or mental image of a primitive notion, to give a foundation to build the notion on which would formally be based on the (unstated) axioms. Descriptions of this type may be referred to, by some authors, as definitions in this informal style of presentation. These are not true definitions, and could not be used in formal proofs of statements. The "definition" of line in Euclid's Elements falls into this category. Even in the case where a specific geometry is being considered (for example, Euclidean geometry), there is no generally accepted agreement among authors as to what an informal description of a line should be when the subject is not being treated formally.
In Euclidean geometry
When geometry was first formalized by Euclid in the Elements, he defined a general line (straight or curved) to be "breadthless length" with a straight line being a line "which lies evenly with the points on itself". These definitions serve little purpose, since they use terms which are not by themselves defined. In fact, Euclid himself did not use these definitions in this work, and probably included them just to make it clear to the reader what was being discussed. In modern geometry, a line is simply taken as an undefined object with properties given by axioms, but is sometimes defined as a set of points obeying a linear relationship when some other fundamental concept is left undefined.
In an axiomatic formulation of Euclidean geometry, such as that of Hilbert (Euclid's original axioms contained various flaws which have been corrected by modern mathematicians) a line is stated to have certain properties which relate it to other lines and points. For example, for any two distinct points, there is a unique line containing them, and any two distinct lines intersect in at most one point. In two dimensions (i.e., the Euclidean plane), two lines which do not intersect are called parallel. In higher dimensions, two lines that do not intersect are parallel if they are contained in a plane, or skew if they are not.
Any collection of finitely many lines partitions the plane into convex polygons (possibly unbounded); this partition is known as an arrangement of lines.
In Cartesian coordinates
Lines in a Cartesian plane or, more generally, in affine coordinates, are characterized by linear equations. More precisely, every line (including vertical lines) is the set of all points whose coordinates (x, y) satisfy a linear equation; that is,
where a, b and c are fixed real numbers (called coefficients) such that a and b are not both zero. Using this form, vertical lines correspond to equations with b = 0.
One can further suppose either c = 1 or c = 0, by dividing everything by c if it is not zero.
There are many variant ways to write the equation of a line which can all be converted from one to another by algebraic manipulation. The above form is sometimes called the standard form. If the constant term is put on the left, the equation becomes
and this is sometimes called the general form of the equation. However, this terminology is not universally accepted, and many authors do not distinguish these two forms.
These forms (see Linear equation for other forms) are generally named by the type of information (data) about the line that is needed to write down the form. Some of the important data of a line is its slope, x-intercept, known points on the line and y-intercept.
The equation of the line passing through two different points and may be written as
- .
If x0 ≠ x1, this equation may be rewritten as
or
Parametric equations
Parametric equations are also used to specify lines, particularly in those in three dimensions or more because in more than two dimensions lines cannot be described by a single linear equation.
In three dimensions lines are frequently described by parametric equations:
where:
- x, y, and z are all functions of the independent variable t which ranges over the real numbers.
- (x0, y0, z0) is any point on the line.
- a, b, and c are related to the slope of the line, such that the direction vector (a, b, c) is parallel to the line.
Parametric equations for lines in higher dimensions are similar in that they are based on the specification of one point on the line and a direction vector.
As a note, lines in three dimensions may also be described as the simultaneous solutions of two linear equations
such that and are not proportional (the relations imply ). This follows since in three dimensions a single linear equation typically describes a plane and a line is what is common to two distinct intersecting planes.
Slope-intercept form
In two dimensions, the equation for non-vertical lines is often given in the slope-intercept form:
where:
- m is the slope or gradient of the line.
- b is the y-intercept of the line.
- x is the independent variable of the function y = f(x).
The slope of the line through points and , when , is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m = (y_b - y_a)/(x_b - x_a)} and the equation of this line can be written Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = m (x - x_a) + y_a} .
Normal form
The normal form (also called the Hesse normal form, after the German mathematician Ludwig Otto Hesse), is based on the normal segment for a given line, which is defined to be the line segment drawn from the origin perpendicular to the line. This segment joins the origin with the closest point on the line to the origin. The normal form of the equation of a straight line on the plane is given by:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \cos \varphi + y \sin \varphi - p = 0 ,}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} is the angle of inclination of the normal segment (the oriented angle from the unit vector of the x-axis to this segment), and p is the (positive) length of the normal segment. The normal form can be derived from the standard form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax+by=c} by dividing all of the coefficients by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{c}{|c|}\sqrt{a^2 + b^2}.}
Unlike the slope-intercept and intercept forms, this form can represent any line but also requires only two finite parameters, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} and p, to be specified. If p > 0, then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} is uniquely defined modulo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \pi } . On the other hand, if the line is through the origin (c = p = 0), one drops the c/|c| term to compute Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin\varphi} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\varphi} , and it follows that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} is only defined modulo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } .
In polar coordinates
In a Cartesian plane, polar coordinates (r, θ) are related to Cartesian coordinates by the equations
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=r\cos\theta, \quad y=r\sin\theta.}
In polar coordinates, the equation of a line not passing through the origin—the point with coordinates (0, 0)—can be written
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\frac p {\cos (\theta-\varphi)},}
with r > 0 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi-\pi/2 < \theta < \varphi + \pi/2.} Here, p is the (positive) length of the line segment perpendicular to the line and delimited by the origin and the line, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} is the (oriented) angle from the x-axis to this segment.
It may be useful to express the equation in terms of the angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=\varphi+\pi/2} between the x-axis and the line. In this case, the equation becomes
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\frac p {\sin (\theta-\alpha)},}
with r > 0 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < \theta < \alpha + \pi.}
These equations can be derived from the normal form of the line equation by setting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=r\cos\theta,} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=r\sin\theta,} and then applying the angle difference identity for sine or cosine.
These equations can also be proven geometrically by applying right triangle definitions of sine and cosine to the right triangle that has a point of the line and the origin as vertices, and the line and its perpendicular through the origin as sides.
The previous forms do not apply for a line passing through the origin, but a simpler formula can be written: the polar coordinates Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (r, \theta)} of the points of a line passing through the origin and making an angle of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} with the x-axis, are the pairs Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (r, \theta)} such that
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\ge 0,\qquad \text{and} \quad \theta=\alpha \quad\text{or}\quad \theta=\alpha +\pi.}
As a vector equation
The vector equation of the line through points A and B is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r} = \mathbf{OA} + \lambda\, \mathbf{AB}} (where λ is a scalar).
If a is vector OA and b is vector OB, then the equation of the line can be written: .
A ray starting at point A is described by limiting λ. One ray is obtained if λ ≥ 0, and the opposite ray comes from λ ≤ 0.
In higher dimensions
In three-dimensional space, a first degree equation in the variables x, y, and z defines a plane, so two such equations, provided the planes they give rise to are not parallel, define a line which is the intersection of the planes. More generally, in n-dimensional space n−1 first-degree equations in the n coordinate variables define a line under suitable conditions.
In more general Euclidean space, Rn (and analogously in every other affine space), the line L passing through two different points a and b (considered as vectors) is the subset
The direction of the line is from a (t = 0) to b (t = 1), or in other words, in the direction of the vector b − a. Different choices of a and b can yield the same line.
Collinear points
Three points are said to be collinear if they lie on the same line. Three points usually determine a plane, but in the case of three collinear points this does not happen.
In affine coordinates, in n-dimensional space the points X = (x1, x2, ..., xn), Y = (y1, y2, ..., yn), and Z = (z1, z2, ..., zn) are collinear if the matrix
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} 1 & x_1 & x_2 & \dots & x_n \\ 1 & y_1 & y_2 & \dots & y_n \\ 1 & z_1 & z_2 & \dots & z_n \end{bmatrix} }
has a rank less than 3. In particular, for three points in the plane (n = 2), the above matrix is square and the points are collinear if and only if its determinant is zero.
Equivalently for three points in a plane, the points are collinear if and only if the slope between one pair of points equals the slope between any other pair of points (in which case the slope between the remaining pair of points will equal the other slopes). By extension, k points in a plane are collinear if and only if any (k–1) pairs of points have the same pairwise slopes.
In Euclidean geometry, the Euclidean distance d(a,b) between two points a and b may be used to express the collinearity between three points by:
- The points a, b and c are collinear if and only if d(x,a) = d(c,a) and d(x,b) = d(c,b) implies x = c.
However, there are other notions of distance (such as the Manhattan distance) for which this property is not true.
In the geometries where the concept of a line is a primitive notion, as may be the case in some synthetic geometries, other methods of determining collinearity are needed.
Types of lines
In a sense, all lines in Euclidean geometry are equal, in that, without coordinates, one can not tell them apart from one another. However, lines may play special roles with respect to other objects in the geometry and be divided into types according to that relationship. For instance, with respect to a conic (a circle, ellipse, parabola, or hyperbola), lines can be:
- tangent lines, which touch the conic at a single point;
- secant lines, which intersect the conic at two points and pass through its interior;
- exterior lines, which do not meet the conic at any point of the Euclidean plane; or
- a directrix, whose distance from a point helps to establish whether the point is on the conic.
In the context of determining parallelism in Euclidean geometry, a transversal is a line that intersects two other lines that may or not be parallel to each other.
For more general algebraic curves, lines could also be:
- i-secant lines, meeting the curve in i points counted without multiplicity, or
- asymptotes, which a curve approaches arbitrarily closely without touching it.
With respect to triangles we have:
- the Euler line,
- the Simson lines, and
- central lines.
For a convex quadrilateral with at most two parallel sides, the Newton line is the line that connects the midpoints of the two diagonals.
For a hexagon with vertices lying on a conic we have the Pascal line and, in the special case where the conic is a pair of lines, we have the Pappus line.
Parallel lines are lines in the same plane that never cross. Intersecting lines share a single point in common. Coincidental lines coincide with each other—every point that is on either one of them is also on the other.
Perpendicular lines are lines that intersect at right angles.
In three-dimensional space, skew lines are lines that are not in the same plane and thus do not intersect each other.
In projective geometry
In many models of projective geometry, the representation of a line rarely conforms to the notion of the "straight curve" as it is visualised in Euclidean geometry. In elliptic geometry we see a typical example of this. In the spherical representation of elliptic geometry, lines are represented by great circles of a sphere with diametrically opposite points identified. In a different model of elliptic geometry, lines are represented by Euclidean planes passing through the origin. Even though these representations are visually distinct, they satisfy all the properties (such as, two points determining a unique line) that make them suitable representations for lines in this geometry.
Extensions
Ray
Given a line and any point A on it, we may consider A as decomposing this line into two parts. Each such part is called a ray and the point A is called its initial point. It is also known as half-line, a one-dimensional half-space. The point A is considered to be a member of the ray. Intuitively, a ray consists of those points on a line passing through A and proceeding indefinitely, starting at A, in one direction only along the line. However, in order to use this concept of a ray in proofs a more precise definition is required.
Given distinct points A and B, they determine a unique ray with initial point A. As two points define a unique line, this ray consists of all the points between A and B (including A and B) and all the points C on the line through A and B such that B is between A and C. This is, at times, also expressed as the set of all points C on the line determined by A and B such that A is not between B and C. A point D, on the line determined by A and B but not in the ray with initial point A determined by B, will determine another ray with initial point A. With respect to the AB ray, the AD ray is called the opposite ray.
Thus, we would say that two different points, A and B, define a line and a decomposition of this line into the disjoint union of an open segment (A, B) and two rays, BC and AD (the point D is not drawn in the diagram, but is to the left of A on the line AB). These are not opposite rays since they have different initial points.
In Euclidean geometry two rays with a common endpoint form an angle.
The definition of a ray depends upon the notion of betweenness for points on a line. It follows that rays exist only for geometries for which this notion exists, typically Euclidean geometry or affine geometry over an ordered field. On the other hand, rays do not exist in projective geometry nor in a geometry over a non-ordered field, like the complex numbers or any finite field.
Line segment
A line segment is a part of a line that is bounded by two distinct end points and contains every point on the line between its end points. Depending on how the line segment is defined, either of the two end points may or may not be part of the line segment. Two or more line segments may have some of the same relationships as lines, such as being parallel, intersecting, or skew, but unlike lines they may be none of these, if they are coplanar and either do not intersect or are collinear.
Geodesics
The "shortness" and "straightness" of a line, interpreted as the property that the distance along the line between any two of its points is minimized (see triangle inequality), can be generalized and leads to the concept of geodesics in metric spaces.
Angle
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in the plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.
Angle is also used to designate the measure of an angle or of a rotation. This measure is the ratio of the length of a circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation.
Identifying angles
In mathematical expressions, it is common to use Greek letters (α, β, γ, θ, φ, . . . ) as variables denoting the size of some angle (to avoid confusion with its other meaning, the symbol π is typically not used for this purpose). Lower case Roman letters (a, b, c, . . . ) are also used, as are upper case Roman letters in the context of polygons. See the figures in this article for examples.
In geometric figures, angles may also be identified by the labels attached to the three points that define them. For example, the angle at vertex A enclosed by the rays AB and AC (i.e. the lines from point A to point B and point A to point C) is denoted ∠BAC or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{\rm BAC}} . Where there is no risk of confusion, the angle may sometimes be referred to simply by its vertex (in this case "angle A").
Potentially, an angle denoted as, say, ∠BAC, might refer to any of four angles: the clockwise angle from B to C, the anticlockwise angle from B to C, the clockwise angle from C to B, or the anticlockwise angle from C to B, where the direction in which the angle is measured determines its sign (see Positive and negative angles). However, in many geometrical situations, it is obvious from context that the positive angle less than or equal to 180 degrees is meant, in which case no ambiguity arises. Otherwise, a convention may be adopted so that ∠BAC always refers to the anticlockwise (positive) angle from B to C, and ∠CAB the anticlockwise (positive) angle from C to B.
Types of angles
Individual angles
There is some common terminology for angles, whose measure is always non-negative (see Positive and negative angles):
- An angle equal to 0° or not turned is called a zero angle.
- An angle smaller than a right angle (less than 90°) is called an acute angle ("acute" meaning "sharp").
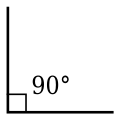
- An angle equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{4}} turn (90° or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\pi}{2}} radians) is called a right angle. Two lines that form a right angle are said to be normal, orthogonal, or perpendicular.
- An angle larger than a right angle and smaller than a straight angle (between 90° and 180°) is called an obtuse angle ("obtuse" meaning "blunt").
- An angle equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}} turn (180° or π radians) is called a straight angle.
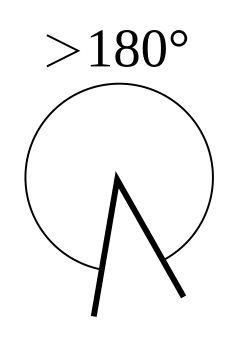
- An angle larger than a straight angle but less than 1 turn (between 180° and 360°) is called a reflex angle.
- An angle equal to 1 turn (360° or 2π radians) is called a full angle, complete angle, round angle or a perigon.
- An angle that is not a multiple of a right angle is called an oblique angle.
The names, intervals, and measuring units are shown in the table below:
| Name | zero | acute | right angle | obtuse | straight | reflex | perigon | |||
| Unit | Interval | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| turn | 0 turn | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left (0, \tfrac{1}{4} \right ) } turn | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{4} } turn | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( \tfrac{1}{4}, \tfrac{1}{2} \right ) } turn | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2} } turn | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( \tfrac{1}{2}, 1 \right )} turn | 1 turn | |||
| radian | 0 rad | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left (0, \tfrac{1}{2} \pi \right ) } rad | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2} \pi } rad | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( \tfrac{1}{2} \pi, \pi \right ) } rad | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } rad | (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \pi } ) rad | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \pi } rad | |||
| degree | 0° | (0, 90)° | 90° | (90, 180)° | 180° | (180, 360)° | 360° | |||
| gon | 0g | (0, 100)g | 100g | (100, 200)g | 200g | (200, 400)g | 400g | |||
Equivalence angle pairs
- Angles that have the same measure (i.e. the same magnitude) are said to be equal or congruent. An angle is defined by its measure and is not dependent upon the lengths of the sides of the angle (e.g. all right angles are equal in measure).
- Two angles that share terminal sides, but differ in size by an integer multiple of a turn, are called coterminal angles.
- A reference angle is the acute version of any angle determined by repeatedly subtracting or adding straight angle (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}} turn, 180°, or π radians), to the results as necessary, until the magnitude of the result is an acute angle, a value between 0 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{4}} turn, 90°, or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {\pi}{2}} radians. For example, an angle of 30 degrees has a reference angle of 30 degrees, and an angle of 150 degrees also has a reference angle of 30 degrees (180–150). An angle of 750 degrees has a reference angle of 30 degrees (750–720).
Vertical and adjacent angle pairs
When two straight lines intersect at a point, four angles are formed. Pairwise these angles are named according to their location relative to each other.
- A pair of angles opposite each other, formed by two intersecting straight lines that form an "X"-like shape, are called vertical angles or opposite angles or vertically opposite angles. They are abbreviated as vert. opp. ∠s.
- The equality of vertically opposite angles is called the vertical angle theorem. Eudemus of Rhodes attributed the proof to Thales of Miletus. The proposition showed that since both of a pair of vertical angles are supplementary to both of the adjacent angles, the vertical angles are equal in measure. According to a historical note, when Thales visited Egypt, he observed that whenever the Egyptians drew two intersecting lines, they would measure the vertical angles to make sure that they were equal. Thales concluded that one could prove that all vertical angles are equal if one accepted some general notions such as:
- All straight angles are equal.
- Equals added to equals are equal.
- Equals subtracted from equals are equal.
- When two adjacent angles form a straight line, they are supplementary. Therefore, if we assume that the measure of angle A equals x, then the measure of angle C would be 180° − x. Similarly, the measure of angle D would be 180° − x. Both angle C and angle D have measures equal to 180° − x and are congruent. Since angle B is supplementary to both angles C and D, either of these angle measures may be used to determine the measure of Angle B. Using the measure of either angle C or angle D, we find the measure of angle B to be 180° − (180° − x) = 180° − 180° + x = x. Therefore, both angle A and angle B have measures equal to x and are equal in measure.
- Adjacent angles, often abbreviated as adj. ∠s, are angles that share a common vertex and edge but do not share any interior points. In other words, they are angles that are side by side, or adjacent, sharing an "arm". Adjacent angles which sum to a right angle, straight angle, or full angle are special and are respectively called complementary, supplementary and explementary angles (see Combining angle pairs below).
A transversal is a line that intersects a pair of (often parallel) lines, and is associated with alternate interior angles, corresponding angles, interior angles, and exterior angles.
Combining angle pairs
Three special angle pairs involve the summation of angles:
- Complementary angles are angle pairs whose measures sum to one right angle (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{4}} turn, 90°, or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\pi}{2}} radians). If the two complementary angles are adjacent, their non-shared sides form a right angle. In Euclidean geometry, the two acute angles in a right triangle are complementary, because the sum of internal angles of a triangle is 180 degrees, and the right angle itself accounts for 90 degrees.
- The adjective complementary is from Latin complementum, associated with the verb complere, "to fill up". An acute angle is "filled up" by its complement to form a right angle.
- The difference between an angle and a right angle is termed the complement of the angle.
- If angles A and B are complementary, the following relationships hold:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} & \sin^2A + \sin^2B = 1 & & \cos^2A + \cos^2B = 1 \\[3pt] & \tan A = \cot B & & \sec A = \csc B \end{align} }
- (The tangent of an angle equals the cotangent of its complement and its secant equals the cosecant of its complement.)
- The prefix "co-" in the names of some trigonometric ratios refers to the word "complementary".
- Two angles that sum to a straight angle (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}} turn, 180°, or π radians) are called supplementary angles.
- If the two supplementary angles are adjacent (i.e. have a common vertex and share just one side), their non-shared sides form a straight line. Such angles are called a linear pair of angles. However, supplementary angles do not have to be on the same line, and can be separated in space. For example, adjacent angles of a parallelogram are supplementary, and opposite angles of a cyclic quadrilateral (one whose vertices all fall on a single circle) are supplementary.
- If a point P is exterior to a circle with center O, and if the tangent lines from P touch the circle at points T and Q, then ∠TPQ and ∠TOQ are supplementary.
- The sines of supplementary angles are equal. Their cosines and tangents (unless undefined) are equal in magnitude but have opposite signs.
- In Euclidean geometry, any sum of two angles in a triangle is supplementary to the third, because the sum of internal angles of a triangle is a straight angle.
- Two angles that sum to a complete angle (1 turn, 360°, or 2π radians) are called explementary angles or conjugate angles.
- The difference between an angle and a complete angle is termed the explement of the angle or conjugate of an angle.
- An angle that is part of a simple polygon is called an interior angle if it lies on the inside of that simple polygon. A simple concave polygon has at least one interior angle that is a reflex angle.
- In Euclidean geometry, the measures of the interior angles of a triangle add up to π radians, 180°, or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}} turn; the measures of the interior angles of a simple convex quadrilateral add up to 2π radians, 360°, or 1 turn. In general, the measures of the interior angles of a simple convex polygon with n sides add up to (n − 2)π radians, or (n − 2)180 degrees, (n − 2)2 right angles, or (n − 2)Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}} turn.
- The supplement of an interior angle is called an exterior angle, that is, an interior angle and an exterior angle form a linear pair of angles. There are two exterior angles at each vertex of the polygon, each determined by extending one of the two sides of the polygon that meet at the vertex; these two angles are vertical and hence are equal. An exterior angle measures the amount of rotation one has to make at a vertex to trace out the polygon. If the corresponding interior angle is a reflex angle, the exterior angle should be considered negative. Even in a non-simple polygon it may be possible to define the exterior angle, but one will have to pick an orientation of the plane (or surface) to decide the sign of the exterior angle measure.
- In Euclidean geometry, the sum of the exterior angles of a simple convex polygon, if only one of the two exterior angles is assumed at each vertex, will be one full turn (360°). The exterior angle here could be called a supplementary exterior angle. Exterior angles are commonly used in Logo Turtle programs when drawing regular polygons.
- In a triangle, the bisectors of two exterior angles and the bisector of the other interior angle are concurrent (meet at a single point).
- In a triangle, three intersection points, each of an external angle bisector with the opposite extended side, are collinear.
- In a triangle, three intersection points, two of them between an interior angle bisector and the opposite side, and the third between the other exterior angle bisector and the opposite side extended, are collinear.
- Some authors use the name exterior angle of a simple polygon to simply mean the explement exterior angle (not supplement!) of the interior angle. This conflicts with the above usage.
- The angle between two planes (such as two adjacent faces of a polyhedron) is called a dihedral angle. It may be defined as the acute angle between two lines normal to the planes.
- The angle between a plane and an intersecting straight line is equal to ninety degrees minus the angle between the intersecting line and the line that goes through the point of intersection and is normal to the plane.
Measuring angles
The size of a geometric angle is usually characterized by the magnitude of the smallest rotation that maps one of the rays into the other. Angles that have the same size are said to be equal or congruent or equal in measure.
In some contexts, such as identifying a point on a circle or describing the orientation of an object in two dimensions relative to a reference orientation, angles that differ by an exact multiple of a full turn are effectively equivalent. In other contexts, such as identifying a point on a spiral curve or describing the cumulative rotation of an object in two dimensions relative to a reference orientation, angles that differ by a non-zero multiple of a full turn are not equivalent.
In order to measure an angle θ, a circular arc centered at the vertex of the angle is drawn, e.g. with a pair of compasses. The ratio of the length s of the arc by the radius r of the circle is the number of radians in the angle. Conventionally, in mathematics and in the SI, the radian is treated as being equal to the dimensionless value 1.
The angle expressed another angular unit may then be obtained by multiplying the angle by a suitable conversion constant of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{k}{2 \pi} } , where k is the measure of a complete turn expressed in the chosen unit (for example, k = 360° for degrees or 400 grad for gradians):
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = \frac{k}{2\pi} \cdot \frac{s}{r}. }
The value of θ thus defined is independent of the size of the circle: if the length of the radius is changed then the arc length changes in the same proportion, so the ratio s/r is unaltered.
In particular, the measure of angle is radian can be also interpreted as the arc length of its corresponding unit circle:
Angle addition postulate
The angle addition postulate states that if B is in the interior of angle AOC, then
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\angle \mathrm{AOC} = m\angle \mathrm{AOB} + m\angle \mathrm{BOC} }
The measure of the angle AOC is the sum of the measure of angle AOB and the measure of angle BOC.
Units
Throughout history, angles have been measured in many different units. These are known as angular units, with the most contemporary units being the degree ( ° ), the radian (rad), and the gradian (grad), though many others have been used throughout history.
Angles expressed in radians are dimensionless for dimensional analysis.
Most units of angular measurement are defined such that one turn (i.e. one full circle) is equal to n units, for some whole number n. The two exceptions are the radian (and its decimal submultiples) and the diameter part.
One radian is the angle subtended by an arc of a circle that has the same length as the circle's radius. The radian is the derived quantity of angular measurement in the SI system. By definition, it is dimensionless, though it may be specified as rad to avoid ambiguity. Angles measured in degrees, are shown with the symbol °. Subdivisions of the degree are minute (symbol ′, 1′ = 1/60°) and second {symbol ″, 1″ = 1/3600°}. An angle of 360° corresponds to the angle subtended by a full circle, and is equal to 2π radians, or 400 gradians.
Other units used to represent angles are listed in the following table. These units are defined such that the number of turns is equivalent to a full circle.
| name | number in one turn | rotation angle | description |
|---|---|---|---|
| Turn | 1 | 360° | The turn, also cycle, full circle, revolution, and rotation, is complete circular movement or measure (as to return to the same point) with circle or ellipse. A turn is abbreviated τ, cyc, rev, or rot depending on the application.. The symbol τ can also be used as a mathematical constant to represent 2π radians. |
| Multiples of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } | 2 | 180° | The multiples of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } (MULFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } ) unit is implemented in the RPN scientific calculator WP 43S. See also: IEEE 754 recommended operations |
| Quadrant | 4 | 90° | One quadrant is a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{4}} turn and also known as a right angle. The quadrant is the unit used in Euclid's Elements. In German the symbol ∟ has been used to denote a quadrant. It is the unit used in Euclid's Elements. 1 quad = 90° = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\pi}{2}} rad = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{4}} turn = 100 grad. |
| Sextant | 6 | 60° | The sextant was the unit used by the Babylonians, The degree, minute of arc and second of arc are sexagesimal subunits of the Babylonian unit. It is especially easy to construct with ruler and compasses. It is the angle of the equilateral triangle or is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{6}} turn. 1 Babylonian unit = 60° = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\pi}{3}} rad ≈ 1.047197551 rad. |
| Radian | 2π | 57°17′ | The radian is determined by the circumference of a circle that is equal in length to the radius of the circle (n = 2π = 6.283...). It is the angle subtended by an arc of a circle that has the same length as the circle's radius. The symbol for radian is rad. One turn is 2π radians, and one radian is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{180^ \circ}{\pi}} , or about 57.2958 degrees. In mathematical texts, angles are often treated as being dimensionless with the radian equal to one, resulting in the unit rad often being omitted. The radian is used in virtually all mathematical work beyond simple practical geometry, due, for example, to the pleasing and "natural" properties that the trigonometric functions display when their arguments are in radians. The radian is the (derived) unit of angular measurement in the SI, which also treats angle as being dimensionless. |
| Hexacontade | 60 | 6° | The hexacontade is a unit used by Eratosthenes. It is equal to 6°, so that a whole turn was divided into 60 hexacontades. |
| Binary degree | 256 | 1°33'45" | The binary degree, also known as the binary radian (or brad). The binary degree is used in computing so that an angle can be efficiently represented in a single byte (albeit to limited precision). Other measures of angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n. It is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{256}} of a turn. |
| Degree | 360 | 1° | One advantage of this old sexagesimal subunit is that many angles common in simple geometry are measured as a whole number of degrees. Fractions of a degree may be written in normal decimal notation (e.g. 3.5° for three and a half degrees), but the "minute" and "second" sexagesimal subunits of the "degree-minute-second" system are also in use, especially for geographical coordinates and in astronomy and ballistics (n = 360) The degree, denoted by a small superscript circle (°), is 1/360 of a turn, so one turn is 360°. The case of degrees for the formula given earlier, a degree of n = 360° units is obtained by setting k = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{360^ \circ}{2 \pi}} . |
| Grad | 400 | 0°54′ | The grad, also called grade, gradian, or gon. a right angle is 100 grads. It is a decimal subunit of the quadrant. A kilometre was historically defined as a centi-grad of arc along a meridian of the Earth, so the kilometer is the decimal analog to the sexagesimal nautical mile (n = 400). The grad is used mostly in triangulation and continental surveying. |
| Minute of arc | 21,600 | 0°1′ | The minute of arc (or MOA, arcminute, or just minute) is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{60} } of a degree. A nautical mile was historically defined as a minute of arc along a great circle of the Earth (n = 21,600). The arcminute is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{60} } of a degree = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{21,600} } turn. It is denoted by a single prime ( ′ ). For example, 3° 30′ is equal to 3 × 60 + 30 = 210 minutes or 3 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{30}{60} } = 3.5 degrees. A mixed format with decimal fractions is also sometimes used, e.g. 3° 5.72′ = 3 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{5.72}{60} } degrees. A nautical mile was historically defined as an arcminute along a great circle of the Earth. |
| Second of arc | 1,296,000 | 0°0′1″ | The second of arc (or arcsecond, or just second) is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{60} } of a minute of arc and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{3600} } of a degree (n = 1,296,000). The arcsecond (or second of arc, or just second) is of an arcminute and of a degree. It is denoted by a double prime ( ″ ). For example, 3° 7′ 30″ is equal to 3 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{7}{60} } + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{30}{3600} } degrees, or 3.125 degrees. |
Other descriptors
- Hour angle (n = 24): The astronomical hour angle is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{24} } turn. As this system is amenable to measuring objects that cycle once per day (such as the relative position of stars), the sexagesimal subunits are called minute of time and second of time. These are distinct from, and 15 times larger than, minutes and seconds of arc. 1 hour = 15° = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\pi}{12} } rad = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{6} } quad = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{24} } turn = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 16 \tfrac{2}{3} } grad.
- (Compass) point or wind (n = 32): The point, used in navigation, is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{32} } of a turn. 1 point = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{8} } of a right angle = 11.25° = 12.5 grad. Each point is subdivided in four quarter-points so that 1 turn equals 128 quarter-points.
- Pechus (n = 144–180): The pechus was a Babylonian unit equal to about 2° or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {2 \tfrac{1}{2}} ^ \circ } .
- Tau, the number of radians in one turn (1 turn = τ rad), τ = 2π.
- Chi, an old Chinese angle measurement.
- Diameter part (n = 376.99...): The diameter part (occasionally used in Islamic mathematics) is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{60} } radian. One "diameter part" is approximately 0.95493°. There are about 376.991 diameter parts per turn.
- Milliradian and derived definitions: The true milliradian is defined a thousandth of a radian, which means that a rotation of one turn would equal exactly 2000π mil (or approximately 6283.185 mil), and almost all scope sights for firearms are calibrated to this definition. In addition there are three other derived definitions used for artillery and navigation which are approximately equal to a milliradian. Under these three other definitions one turn makes up for exactly 6000, 6300 or 6400 mils, which equals spanning the range from 0.05625 to 0.06 degrees (3.375 to 3.6 minutes). In comparison, the true milliradian is approximately 0.05729578 degrees (3.43775 minutes). One "NATO mil" is defined as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{6400} } of a circle. Just like with the true milliradian, each of the other definitions exploits the mil's useful property of subtensions, i.e. that the value of one milliradian approximately equals the angle subtended by a width of 1 meter as seen from 1 km away Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( \tfrac{2 \pi}{6400} = 0.0009817 \ldots \approx \tfrac{1}{1000} \right ) } .
- Akhnam and zam. In old Arabia a turn was subdivided in 32 Akhnam and each akhnam was subdivided in 7 zam, so that a turn is 224 zam.
Signed angles
Although the definition of the measurement of an angle does not support the concept of a negative angle, it is frequently useful to impose a convention that allows positive and negative angular values to represent orientations and/or rotations in opposite directions relative to some reference.
In a two-dimensional Cartesian coordinate system, an angle is typically defined by its two sides, with its vertex at the origin. The initial side is on the positive x-axis, while the other side or terminal side is defined by the measure from the initial side in radians, degrees, or turns. With positive angles representing rotations toward the positive y-axis and negative angles representing rotations toward the negative y-axis. When Cartesian coordinates are represented by standard position, defined by the x-axis rightward and the y-axis upward, positive rotations are anticlockwise and negative rotations are clockwise.
In many contexts, an angle of −θ is effectively equivalent to an angle of "one full turn minus θ". For example, an orientation represented as −45° is effectively equivalent to an orientation represented as 360° − 45° or 315°. Although the final position is the same, a physical rotation (movement) of −45° is not the same as a rotation of 315° (for example, the rotation of a person holding a broom resting on a dusty floor would leave visually different traces of swept regions on the floor).
In three-dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined relative to some reference, which is typically a vector passing through the angle's vertex and perpendicular to the plane in which the rays of the angle lie.
In navigation, bearings or azimuth are measured relative to north. By convention, viewed from above, bearing angles are positive clockwise, so a bearing of 45° corresponds to a north-east orientation. Negative bearings are not used in navigation, so a north-west orientation corresponds to a bearing of 315°.
Alternative ways of measuring the size of an angle
There are several alternatives to measuring the size of an angle by the angle of rotation. The slope or gradient is equal to the tangent of the angle, or sometimes (rarely) the sine; a gradient is often expressed as a percentage. For very small values (less than 5%), the grade of a slope is approximately the measure of the angle in radians.
In rational geometry the spread between two lines is defined as the square of the sine of the angle between the lines. As the sine of an angle and the sine of its supplementary angle are the same, any angle of rotation that maps one of the lines into the other leads to the same value for the spread between the lines.
Astronomical approximations
Astronomers measure angular separation of objects in degrees from their point of observation.
- 0.5° is approximately the width of the sun or moon.
- 1° is approximately the width of a little finger at arm's length.
- 10° is approximately the width of a closed fist at arm's length.
- 20° is approximately the width of a handspan at arm's length.
These measurements clearly depend on the individual subject, and the above should be treated as rough rule of thumb approximations only.
In astronomy, right ascension and declination are usually measured in angular units, expressed in terms of time, based on a 24-hour day.
| Unit | Symbol | Degree | Radians | Circle | Other |
|---|---|---|---|---|---|
| Hour | h | 15° | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {\pi}{12} } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{24} } | |
| Minute | m | 0°15' | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {\pi}{720} } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {1}{1,440} } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {1}{60} } hour |
| Second | s | 0°0'15" | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {\pi}{43,200} } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {1}{86,400} } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {1}{60} } minute |
Measurements that are not angular units
Not all angle measurements are angular units, for an angular measurement, it is definitional that the angle addition postulate holds.
Some angle measurements where the angle addition postulate does not hold include:
- Trigonometric functions
- Slope
Angles between curves
The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection. Various names (now rarely, if ever, used) have been given to particular cases:—amphicyrtic (Gr. ἀμφί, on both sides, κυρτός, convex) or cissoidal (Gr. κισσός, ivy), biconvex; xystroidal or sistroidal (Gr. ξυστρίς, a tool for scraping), concavo-convex; amphicoelic (Gr. κοίλη, a hollow) or angulus lunularis, biconcave.
Bisecting and trisecting angles
The ancient Greek mathematicians knew how to bisect an angle (divide it into two angles of equal measure) using only a compass and straightedge, but could only trisect certain angles. In 1837 Pierre Wantzel showed that for most angles this construction cannot be performed.
Dot product and generalisations
In the Euclidean space, the angle θ between two Euclidean vectors u and v is related to their dot product and their lengths by the formula
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u} \cdot \mathbf{v} = \cos(\theta) \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .}
This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their normal vectors and between skew lines from their vector equations.
Inner product
To define angles in an abstract real inner product space, we replace the Euclidean dot product ( · ) by the inner product Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \cdot , \cdot \rangle } , i.e.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \mathbf{u} , \mathbf{v} \rangle = \cos(\theta)\ \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .}
In a complex inner product space, the expression for the cosine above may give non-real values, so it is replaced with
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{Re} \left( \langle \mathbf{u} , \mathbf{v} \rangle \right) = \cos(\theta) \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .}
or, more commonly, using the absolute value, with
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| \langle \mathbf{u} , \mathbf{v} \rangle \right| = \left| \cos(\theta) \right| \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| .}
The latter definition ignores the direction of the vectors and thus describes the angle between one-dimensional subspaces Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{span}(\mathbf{u})} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{span}(\mathbf{v})} spanned by the vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} correspondingly.
Angles between subspaces
The definition of the angle between one-dimensional subspaces Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{span}(\mathbf{u})} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{span}(\mathbf{v})} given by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| \langle \mathbf{u} , \mathbf{v} \rangle \right| = \left| \cos(\theta) \right| \left\| \mathbf{u} \right\| \left\| \mathbf{v} \right\| }
in a Hilbert space can be extended to subspaces of any finite dimensions. Given two subspaces Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{U} } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{W} } with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim ( \mathcal{U}) := k \leq \dim ( \mathcal{W}) := l } , this leads to a definition of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} angles called canonical or principal angles between subspaces.
Angles in Riemannian geometry
In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where U and V are tangent vectors and gij are the components of the metric tensor G,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \theta = \frac{g_{ij}U^iV^j}{\sqrt{ \left| g_{ij}U^iU^j \right| \left| g_{ij}V^iV^j \right|}}. }
Hyperbolic angle
A hyperbolic angle is an argument of a hyperbolic function just as the circular angle is the argument of a circular function. The comparison can be visualized as the size of the openings of a hyperbolic sector and a circular sector since the areas of these sectors correspond to the angle magnitudes in each case. Unlike the circular angle, the hyperbolic angle is unbounded. When the circular and hyperbolic functions are viewed as infinite series in their angle argument, the circular ones are just alternating series forms of the hyperbolic functions. This weaving of the two types of angle and function was explained by Leonhard Euler in Introduction to the Analysis of the Infinite.
Angles in geography and astronomy
In geography, the location of any point on the Earth can be identified using a geographic coordinate system. This system specifies the latitude and longitude of any location in terms of angles subtended at the center of the Earth, using the equator and (usually) the Greenwich meridian as references.
In astronomy, a given point on the celestial sphere (that is, the apparent position of an astronomical object) can be identified using any of several astronomical coordinate systems, where the references vary according to the particular system. Astronomers measure the angular separation of two stars by imagining two lines through the center of the Earth, each intersecting one of the stars. The angle between those lines can be measured and is the angular separation between the two stars.
In both geography and astronomy, a sighting direction can be specified in terms of a vertical angle such as altitude /elevation with respect to the horizon as well as the azimuth with respect to north.
Astronomers also measure the apparent size of objects as an angular diameter. For example, the full moon has an angular diameter of approximately 0.5°, when viewed from Earth. One could say, "The Moon's diameter subtends an angle of half a degree." The small-angle formula can be used to convert such an angular measurement into a distance/size ratio.
Licensing
Content obtained and/or adapted from:
- Line (geometry), Wikipedia under a CC BY-SA license
- Angle, Wikipedia under a CC BY-SA license