Difference between revisions of "Inverse Trigonometric Functions"
(Created page with "In mathematics, the '''inverse trigonometric functions''' (occasionally also called '''arcus functions''', '''antitrigonometric functions''' or '''cyclometric functions''' are...") |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | In mathematics, the '''inverse trigonometric functions''' (occasionally also called '''arcus functions''', '''antitrigonometric functions''' or '''cyclometric functions''' are the | + | In mathematics, the '''inverse trigonometric functions''' (occasionally also called '''arcus functions''', '''antitrigonometric functions''' or '''cyclometric functions''' are the inverse functions of the trigonometric functions (with suitably restricted domains). Specifically, they are the inverses of the sine, cosine, tangent (trigonometry)|tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry. |
==Notation== | ==Notation== | ||
| Line 40: | Line 40: | ||
|- | |- | ||
|} | |} | ||
| − | + | ||
| + | Note: Some authors define the range of arcsecant to be <math> \big( 0 \leq y < \tfrac{\pi}{2} \text{ or } \pi < y \leq \tfrac{3 \pi}{2} \big)</math>, because the tangent function is nonnegative on this domain. This makes some computations more consistent. For example, using this range, <math>\tan(\arcsec(x)) = \sqrt{x^2 - 1},</math> whereas with the range <math> \big( 0 \leq y < \tfrac{\pi}{2} \text{ or } \tfrac{\pi}{2} < y \leq \pi \big) </math>, we would have to write <math>\tan(\arcsec(x)) = \pm \sqrt{x^2 - 1},</math> since tangent is nonnegative on <math>0 \leq y < \tfrac{\pi}{2},</math> but nonpositive on <math>\tfrac{\pi}{2} < y \leq \pi.</math> For a similar reason, the same authors define the range of arccosecant to be <math> \big(- \pi < y \leq - \tfrac{\pi}{2} \text{ or } 0 < y \leq \tfrac{\pi}{2} \big).</math> | ||
If <math>x</math> is allowed to be a complex number, then the range of <math>y</math> applies only to its real part. | If <math>x</math> is allowed to be a complex number, then the range of <math>y</math> applies only to its real part. | ||
| Line 157: | Line 158: | ||
|} | |} | ||
| − | So for example, by using the equality <math>\sin \left(\frac{\pi}{2} - \theta\right) = \cos \theta</math> | + | So for example, by using the equality <math>\sin \left(\frac{\pi}{2} - \theta\right) = \cos \theta</math>, the equation <math>\cos \theta = x</math> can be transformed into <math>\sin \left(\frac{\pi}{2} - \theta\right) = x,</math> which allows for the solution to the equation <math>\;\sin \varphi = x\;</math> (where <math>\varphi := \frac{\pi}{2} - \theta</math>) to be used; that solution being: |
<math>\varphi = (-1)^k \arcsin (x) + \pi k \; \text{ for some } k \in \Z,</math> | <math>\varphi = (-1)^k \arcsin (x) + \pi k \; \text{ for some } k \in \Z,</math> | ||
which becomes: | which becomes: | ||
| Line 163: | Line 164: | ||
where using the fact that <math>(-1)^{k} = (-1)^{-k}</math> and substituting <math>h := - k</math> proves that another solution to <math>\;\cos \theta = x\;</math> is: | where using the fact that <math>(-1)^{k} = (-1)^{-k}</math> and substituting <math>h := - k</math> proves that another solution to <math>\;\cos \theta = x\;</math> is: | ||
<math display="block">\theta ~=~ (-1)^{h+1} \arcsin (x) + \pi h + \frac{\pi}{2} \quad \text{ for some } h \in \Z.</math> | <math display="block">\theta ~=~ (-1)^{h+1} \arcsin (x) + \pi h + \frac{\pi}{2} \quad \text{ for some } h \in \Z.</math> | ||
| − | The substitution <math>\;\arcsin x = \frac{\pi}{2} - \arccos x\;</math> may be used express the right hand side of the above formula in terms of <math>\;\arccos x\;</math> instead of <math>\;\arcsin x.\;</math | + | The substitution <math>\;\arcsin x = \frac{\pi}{2} - \arccos x\;</math> may be used express the right hand side of the above formula in terms of <math>\;\arccos x\;</math> instead of <math>\;\arcsin x.\;</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Relationships between trigonometric functions and inverse trigonometric functions === | === Relationships between trigonometric functions and inverse trigonometric functions === | ||
| Line 435: | Line 377: | ||
* [https://www.youtube.com/watch?v=KbYW9FDm-Zk Derivatives of Inverse Trigonometric Functions], The Organic Chemistry Tutor | * [https://www.youtube.com/watch?v=KbYW9FDm-Zk Derivatives of Inverse Trigonometric Functions], The Organic Chemistry Tutor | ||
| − | == | + | == Licensing == |
| − | + | Content obtained and/or adapted from: | |
| − | + | * [https://en.wikipedia.org/wiki/Inverse_trigonometric_functions Inverse trigonometric functions, Wikipedia] under a CC BY-SA license | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 13:19, 15 January 2022
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions are the inverse functions of the trigonometric functions (with suitably restricted domains). Specifically, they are the inverses of the sine, cosine, tangent (trigonometry)|tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
Notation
Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: arcsin(x), arccos(x), arctan(x), etc. This notation arises from the following geometric relationships: when measuring in radians, an angle of θ radians will correspond to an arc whose length is rθ, where r is the radius of the circle. Thus in the unit circle, "the arc whose cosine is x" is the same as "the angle whose cosine is x", because the length of the arc of the circle in radii is the same as the measurement of the angle in radians. In computer programming languages, the inverse trigonometric functions are often called by the abbreviated forms asin, acos, atan.
The notations sin−1(x), cos−1(x), tan−1(x), etc., as introduced by John Herschel in 1813, are often used as well in English-language sources—conventions consistent with the notation of an inverse function. This might appear to conflict logically with the common semantics for expressions such as sin2(x), which refer to numeric power rather than function composition, and therefore may result in confusion between multiplicative inverse or reciprocal and compositional inverse. The confusion is somewhat mitigated by the fact that each of the reciprocal trigonometric functions has its own name—for example, (cos(x))−1 = sec(x). Nevertheless, certain authors advise against using it for its ambiguity. Another convention used by a few authors is to use an uppercase first letter, along with a −1 superscript: Sin−1(x), Cos−1(x), Tan−1(x), etc. This potentially avoids confusion with the multiplicative inverse, which should be represented by sin−1(x), cos−1(x), etc.
Since 2009, the ISO 80000-2 standard has specified solely the "arc" prefix for the inverse functions.
Basic concepts
Principal values
Since none of the six trigonometric functions are one-to-one, they must be restricted in order to have inverse functions. Therefore, the result ranges of the inverse functions are proper subsets of the domains of the original functions.
For example, using function in the sense of multivalued functions, just as the square root function could be defined from the function is defined so that For a given real number with there are multiple (in fact, countably infinite) numbers such that ; for example, but also etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each in the domain, the expression will evaluate only to a single value, called its principal value. These properties apply to all the inverse trigonometric functions.
The principal inverses are listed in the following table.
| Name | Usual notation | Definition | Domain of for real result | Range of usual principal value (radians) |
Range of usual principal value (degrees) |
|---|---|---|---|---|---|
| arcsine | x = sin(y) | ||||
| arccosine | x = cos(y) | ||||
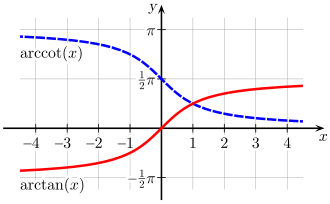
| arctangent | x = tan(y) | all real numbers | |||
| arccotangent | x = cot(y) | all real numbers | |||
| arcsecant | x = sec(y) | ||||
| arccosecant | x = csc(y) |
Note: Some authors define the range of arcsecant to be , because the tangent function is nonnegative on this domain. This makes some computations more consistent. For example, using this range, whereas with the range , we would have to write since tangent is nonnegative on but nonpositive on For a similar reason, the same authors define the range of arccosecant to be
If is allowed to be a complex number, then the range of applies only to its real part.
Solutions to elementary trigonometric equations
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of :
- Sine and cosecant begin their period at (where is an integer), finish it at and then reverse themselves over to
- Cosine and secant begin their period at finish it at and then reverse themselves over to
- Tangent begins its period at finishes it at and then repeats it (forward) over to
- Cotangent begins its period at finishes it at and then repeats it (forward) over to
This periodicity is reflected in the general inverses, where is some integer.
For example, if then for some While if then for some where will be even if and it will be odd if The equations and have the same solutions as and respectively. In all equations above except for those just solved (i.e. except for / and /), the integer in the solution's formula is uniquely determined by (for fixed and ).
- Detailed example and explanation of the "plus or minus" symbol
The solutions to and involve the "plus or minus" symbol whose meaning is now clarified. Only the solution to will be discussed since the discussion for is the same. We are given between and we know that there is an angle in some give interval that satisfies We want to find this The formula for the solution involves:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\theta = \arccos x + 2 \pi k\,}
for some integer Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k,}
or else - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\theta = - \arccos x + 2 \pi k\,} for some integer Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.}
Because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\arccos x \neq 0\,} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,0 < \arccos x \leq \pi\,} exactly one of these two equalities can hold. Additional information about Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} is needed to determine which one holds. For example, suppose that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = 0} and that all that is known about Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} is that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,- \pi \leq \theta \leq \pi\,} (and nothing more is known). Then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \arccos x = \arccos 0 = \frac{\pi}{2}} and moreover, in this particular case Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = 0} (for both the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,+\,} case and the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,-\,} case) and so consequently, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta ~=~ \pm \arccos x + 2 \pi k ~=~ \pm \left(\frac{\pi}{2}\right) + 2\pi (0) ~=~ \pm \frac{\pi}{2}.} This means that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} could be either Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\pi/2\,} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,- \pi/2.} Without additional information it is not possible to determine which of these values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} has. An example of some additional information that could determine the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} would be knowing that the angle is above the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} -axis (in which case Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = \pi/2} ) or alternatively, knowing that it is below the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} -axis (in which case Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = - \pi/2} ).
- Transforming equations
The equations above can be transformed by using the identities
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{func} \ } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{func} (- \theta)} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{func} \left(\frac{\pi}{2} - \theta\right)} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{func} (\pi - \theta)} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{func} (2 \pi - \theta)} | |
|---|---|---|---|---|---|
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle|\,\scriptstyle|} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle|\,\scriptstyle|} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle|\,\scriptstyle|} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle|\,\scriptstyle|} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle|\,\scriptstyle|} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \ } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \sin \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \sin \theta} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \ } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \cos \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \theta} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \tan \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \tan \theta} | ||||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \csc \ } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \csc \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sec \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \csc \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \csc \theta} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sec \ } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sec \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \csc \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \sec \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sec \theta} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cot \ } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \cot \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \cot \theta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \cot \theta} |
So for example, by using the equality Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \left(\frac{\pi}{2} - \theta\right) = \cos \theta} , the equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \theta = x} can be transformed into Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \left(\frac{\pi}{2} - \theta\right) = x,} which allows for the solution to the equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\sin \varphi = x\;} (where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi := \frac{\pi}{2} - \theta} ) to be used; that solution being: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi = (-1)^k \arcsin (x) + \pi k \; \text{ for some } k \in \Z,} which becomes: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{2} - \theta ~=~ (-1)^k \arcsin (x) + \pi k \quad \text{ for some } k \in \Z} where using the fact that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^{k} = (-1)^{-k}} and substituting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h := - k} proves that another solution to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\cos \theta = x\;} is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta ~=~ (-1)^{h+1} \arcsin (x) + \pi h + \frac{\pi}{2} \quad \text{ for some } h \in \Z.} The substitution Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\arcsin x = \frac{\pi}{2} - \arccos x\;} may be used express the right hand side of the above formula in terms of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\arccos x\;} instead of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\arcsin x.\;}
Relationships between trigonometric functions and inverse trigonometric functions
Trigonometric functions of inverse trigonometric functions are tabulated below. A quick way to derive them is by considering the geometry of a right-angled triangle, with one side of length 1 and another side of length Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,} then applying the Pythagorean theorem and definitions of the trigonometric ratios. Purely algebraic derivations are longer. It is worth noting that for arcsecant and arccosecant, the diagram assumes that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is positive, and thus the result has to be corrected through the use of absolute values and the signum (sgn) operation.
Relationships among the inverse trigonometric functions
Complementary angles:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \arccos(x) &= \frac{\pi}{2} - \arcsin(x) \\[0.5em] \arccot(x) &= \frac{\pi}{2} - \arctan(x) \\[0.5em] \arccsc(x) &= \frac{\pi}{2} - \arcsec(x) \end{align}}
Negative arguments:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \arcsin(-x) &= -\arcsin(x) \\ \arccos(-x) &= \pi -\arccos(x) \\ \arctan(-x) &= -\arctan(x) \\ \arccot(-x) &= \pi -\arccot(x) \\ \arcsec(-x) &= \pi -\arcsec(x) \\ \arccsc(-x) &= -\arccsc(x) \end{align}}
Reciprocal arguments:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \arccos\left(\frac{1}{x}\right) &= \arcsec(x) \\[0.3em] \arcsin\left(\frac{1}{x}\right) &= \arccsc(x) \\[0.3em] \arctan\left(\frac{1}{x}\right) &= \frac{\pi}{2} - \arctan(x) = \arccot(x) \, , \text{ if } x > 0 \\[0.3em] \arctan\left(\frac{1}{x}\right) &= -\frac{\pi}{2} - \arctan(x) = \arccot(x) -\pi\, , \text{ if } x < 0 \\[0.3em] \arccot\left(\frac{1}{x}\right) &= \frac{\pi}{2} - \arccot(x) = \arctan(x) \, , \text{ if } x > 0 \\[0.3em] \arccot\left(\frac{1}{x}\right) &= \frac{3\pi}{2} - \arccot(x) = \pi + \arctan(x) \, , \text{ if } x < 0 \\[0.3em] \arcsec\left(\frac{1}{x}\right) &= \arccos(x) \\[0.3em] \arccsc\left(\frac{1}{x}\right) &= \arcsin(x) \end{align}}
Useful identities if one only has a fragment of a sine table:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \arccos(x) &= \arcsin\left(\sqrt{1 - x^2}\right) \, , \text{ if } 0 \leq x \leq 1 \text{ , from which you get } \\ \arccos &\left(\frac{1-x^2}{1 + x^2}\right) = \arcsin \left (\frac{2x}{1 + x^2}\right) \, , \text{ if } 0 \leq x \leq 1 \\ \arcsin &\left(\sqrt{1 - x^2}\right) =\frac{\pi}{2}-\sgn(x)\arcsin(x) \\ \arccos(x) &= \frac{1}{2}\arccos\left(2x^2-1\right) \, , \text{ if } 0 \leq x \leq 1 \\ \arcsin(x) &= \frac{1}{2}\arccos\left(1-2x^2\right) \, , \text{ if } 0 \leq x \leq 1 \\ \arcsin(x) &= \arctan\left(\frac{x}{\sqrt{1 - x^2}}\right) \\ \arccos(x) &= \arctan\left(\frac{\sqrt{1 - x^2}}{x}\right) \\ \arctan(x) &= \arcsin\left(\frac{x}{\sqrt{1 + x^2}}\right) \\ \arccot(x) &= \arccos\left(\frac{x}{\sqrt{1 + x^2}}\right) \end{align}}
Whenever the square root of a complex number is used here, we choose the root with the positive real part (or positive imaginary part if the square was negative real).
A useful form that follows directly from the table above is
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \arctan\left(x\right) = \arccos\left(\sqrt{\frac{1}{1+x^2}}\right)\, , \text{ if } x\geq 0 } .
It is obtained by recognizing that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\left(\arctan\left(x\right)\right) = \sqrt{\frac{1}{1+x^2}} = \cos\left(\arccos\left(\sqrt{\frac{1}{1+x^2}}\right)\right)} .
From the half-angle formula, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan\left(\tfrac{\theta}{2}\right) = \tfrac{\sin(\theta)}{1 + \cos(\theta)}} , we get:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \arcsin(x) &= 2 \arctan\left(\frac{x}{1 + \sqrt{1 - x^2}}\right) \\[0.5em] \arccos(x) &= 2 \arctan\left(\frac{\sqrt{1 - x^2}}{1 + x}\right) \, , \text{ if } -1 < x \leq 1 \\[0.5em] \arctan(x) &= 2 \arctan\left(\frac{x}{1 + \sqrt{1 + x^2}}\right) \end{align}}
Arctangent addition formula
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \arctan(u) \pm \arctan(v) = \arctan\left(\frac{u \pm v}{1 \mp uv}\right) \pmod \pi \, , \quad u v \ne 1 \, .}
This is derived from the tangent addition formula
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan(\alpha \pm \beta) = \frac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha)\tan(\beta)} \, ,}
by letting
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \arctan(u) \, , \quad \beta = \arctan(v) \, .}
In calculus
Derivatives of inverse trigonometric functions
The derivatives for complex values of z are as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{d}{dz} \arcsin(z) &{} = \frac{1}{\sqrt{1-z^2}} \; ; &z &{}\neq -1, +1 \\ \frac{d}{dz} \arccos(z) &{} = -\frac{1}{\sqrt{1-z^2}} \; ; &z &{}\neq -1, +1 \\ \frac{d}{dz} \arctan(z) &{} = \frac{1}{1+z^2} \; ; &z &{}\neq -i, +i\\ \frac{d}{dz} \arccot(z) &{} = -\frac{1}{1+z^2} \; ; &z &{}\neq -i, +i \\ \frac{d}{dz} \arcsec(z) &{} = \frac{1}{z^2 \sqrt{1 - \frac{1}{z^{2}}}} \; ; &z &{}\neq -1, 0, +1 \\ \frac{d}{dz} \arccsc(z) &{} = -\frac{1}{z^2 \sqrt{1 - \frac{1}{z^{2}}}} \; ; &z &{}\neq -1, 0, +1 \end{align}}
Only for real values of x:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{d}{dx} \arcsec(x) &{} = \frac{1}{|x| \sqrt{x^2-1}} \; ; & |x| > 1\\ \frac{d}{dx} \arccsc(x) &{} = -\frac{1}{|x| \sqrt{x^2-1}} \; ; & |x| > 1 \end{align}}
For a sample derivation: if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = \arcsin(x)} , we get:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d \arcsin(x)}{dx} = \frac{d \theta}{d \sin(\theta)} = \frac{d \theta}{\cos(\theta) \, d \theta} = \frac{1}{\cos(\theta)} = \frac{1}{\sqrt{1-\sin^2(\theta)}} = \frac{1}{\sqrt{1-x^2}}}
Expression as definite integrals
Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \arcsin(x) &{}= \int_0^x \frac{1}{\sqrt{1 - z^2}} \, dz \; , & |x| &{} \leq 1\\ \arccos(x) &{}= \int_x^1 \frac{1}{\sqrt{1 - z^2}} \, dz \; , & |x| &{} \leq 1\\ \arctan(x) &{}= \int_0^x \frac{1}{z^2 + 1} \, dz \; ,\\ \arccot(x) &{}= \int_x^\infty \frac{1}{z^2 + 1} \, dz \; ,\\ \arcsec(x) &{}= \int_1^x \frac{1}{z \sqrt{z^2 - 1}} \, dz = \pi + \int_x^{-1} \frac{1}{z \sqrt{z^2 - 1}} \, dz\; , & x &{} \geq 1\\ \arccsc(x) &{}= \int_x^\infty \frac{1}{z \sqrt{z^2 - 1}} \, dz = \int_{-\infty}^x \frac{1}{z \sqrt{z^2 - 1}} \, dz \; , & x &{} \geq 1\\ \end{align}}
When x equals 1, the integrals with limited domains are improper integrals, but still well-defined.
Indefinite integrals of inverse trigonometric functions
For real and complex values of z:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int \arcsin(z) \, dz &{}= z \, \arcsin(z) + \sqrt{1 - z^2} + C\\ \int \arccos(z) \, dz &{}= z \, \arccos(z) - \sqrt{1 - z^2} + C\\ \int \arctan(z) \, dz &{}= z \, \arctan(z) - \frac{1}{2} \ln \left( 1 + z^2 \right) + C\\ \int \arccot(z) \, dz &{}= z \, \arccot(z) + \frac{1}{2} \ln \left( 1 + z^2 \right) + C\\ \int \arcsec(z) \, dz &{}= z \, \arcsec(z) - \ln \left[ z \left( 1 + \sqrt{ \frac{z^2-1}{z^2} } \right) \right] + C\\ \int \arccsc(z) \, dz &{}= z \, \arccsc(z) + \ln \left[ z \left( 1 + \sqrt{ \frac{z^2-1}{z^2} } \right) \right] + C \end{align}}
For real x ≥ 1:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int \arcsec(x) \, dx &{}= x \, \arcsec(x) - \ln \left( x + \sqrt{x^2-1} \right) + C\\ \int \arccsc(x) \, dx &{}= x \, \arccsc(x) + \ln \left( x + \sqrt{x^2-1} \right) + C \end{align}}
For all real x not between -1 and 1:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int \arcsec(x) \, dx &{}= x \, \arcsec(x) - \sgn(x) \ln\left(\left| x + \sqrt{x^2-1}\right|\right) + C\\ \int \arccsc(x) \, dx &{}= x \, \arccsc(x) + \sgn(x) \ln\left(\left| x + \sqrt{x^2-1}\right|\right) + C \end{align}}
The absolute value is necessary to compensate for both negative and positive values of the arcsecant and arccosecant functions. The signum function is also necessary due to the absolute values in the derivatives of the two functions, which create two different solutions for positive and negative values of x. These can be further simplified using the logarithmic definitions of the inverse hyperbolic functions:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int \arcsec(x) \, dx &{}= x \, \arcsec(x) - \operatorname{arcosh}(|x|) + C\\ \int \arccsc(x) \, dx &{}= x \, \arccsc(x) + \operatorname{arcosh}(|x|) + C\\ \end{align}}
The absolute value in the argument of the arcosh function creates a negative half of its graph, making it identical to the signum logarithmic function shown above.
All of these antiderivatives can be derived using integration by parts and the simple derivative forms shown above.
Example
Using Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int u \, dv = u v - \int v \, du} (i.e. integration by parts), set
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} u &= \arcsin(x) & dv &= dx \\ du &= \frac{dx}{\sqrt{1-x^2}} & v &= x \end{align}}
Then
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int \arcsin(x) \, dx = x \arcsin(x) - \int \frac{x}{\sqrt{1-x^2}} \, dx,}
which by the simple substitution Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w=1-x^2,\ dw = -2x\,dx} yields the final result:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int \arcsin(x) \, dx = x \arcsin(x) + \sqrt{1-x^2} + C }
Resources
Review
- Introduction to Inverse Trig Functions, Khan Academy
- Evaluating Inverse Trigonometric Functions, The Organic Chemistry Tutor
Calculus
- Derivatives of Inverse Trigonometric Functions, The Organic Chemistry Tutor
Licensing
Content obtained and/or adapted from:
- Inverse trigonometric functions, Wikipedia under a CC BY-SA license