Difference between revisions of "Functions"
(PASTED FROM WIKIPEDIA FOR TESTING PURPOSES) |
|||
| (19 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | ==Introduction== | |
| − | + | Formally, a function f from a set X to a set Y is defined by a set G of ordered pairs (x, y) such that x ∈ X, y ∈ Y, and every element of X is the first component of exactly one ordered pair in G. In other words, for every x in X, there is exactly one element y such that the ordered pair (x, y) belongs to the set of pairs defining the function f. The set G is called the graph of the function. Formally speaking, it may be identified with the function, but this hides the usual interpretation of a function as a process. Therefore, in common usage, the function is generally distinguished from its graph.}} | |
| − | + | Whenever one quantity uniquely determines the value of another quantity, we have a function. That is, the set <math>X</math> uniquely determines the set <math>Y</math>. You can think of a ''function'' as a kind of machine. You feed the machine raw materials, and the machine changes the raw materials into a finished product. | |
| − | + | ===Functions in everyday life=== | |
| + | Think about dropping a ball from a bridge. At each moment in time, the ball is a height above the ground. The height of the ball is a function of time. It was the job of physicists to come up with a formula for this function. This type of function is called ''real-valued'' since the "finished product" is a number (or, more specifically, a real number). | ||
| − | + | Think about a wind storm. At different places, the wind can be blowing in different directions with different intensities. The direction and intensity of the wind can be thought of as a function of position. This is a function of two real variables (a location is described by two values - an <math>x</math> and a <math>y</math>) which results in a vector (which is something that can be used to hold a direction and an intensity). These functions are studied in multivariable calculus (which is usually studied after a one year college level calculus course). This a vector-valued function of two real variables. | |
| − | + | We will be looking at real-valued functions until studying multivariable calculus. Think of a real-valued function as an ''input-output machine''; you give the function an input, and it gives you an output which is a number (more specifically, a real number). For example, the squaring function takes the input 4 and gives the output value 16. The same squaring function takes the input -1 and gives the output value 1. | |
| + | [[File:Function machine2.svg|thumb|right|This is an intuitive way to understand functions: a machine that makes the input <math>x</math> go through a transformation <math>f</math> into the output <math>f(x)</math>]] | ||
| − | + | === Notation === | |
| + | Functions are used so much that there is a special notation for them. The notation is somewhat ambiguous, so familiarity with it is important in order to understand the intention of an equation or formula. | ||
| − | + | Though there are no strict rules for naming a function, it is standard practice to use the letters <math>f</math> , <math>g</math> , and <math>h</math> to denote functions, and the variable <math>x</math> to denote an independent variable. <math>y</math> is used for both dependent and independent variables. | |
| − | + | When discussing or working with a function <math>f</math> , it's important to know not only the function, but also its independent variable <math>x</math> . Thus, when referring to a function <math>f</math>, you usually do not write <math>f</math>, but instead <math>f(x)</math> . The function is now referred to as "<math>f</math> of <math>x</math>". The name of the function is adjacent to the independent variable (in parentheses). This is useful for indicating the value of the function at a particular value of the independent variable. For instance, if | |
| − | + | :<math>f(x)=7x+1</math> , | |
| + | and if we want to use the value of <math>f</math> for <math>x</math> equal to <math>2</math> , then we would substitute 2 for <math>x</math> on both sides of the definition above and write | ||
| + | :<math>f(2)=7(2)+1=14+1=15</math> | ||
| − | + | This notation is more informative than leaving off the independent variable and writing simply '<math>f</math>' , but can be ambiguous since the parentheses next to <math>f</math> can be misinterpreted as multiplication, <math>2f</math>. To make sure nobody is too confused, follow this procedure: | |
| − | == | + | # Define the function <math>f</math> by equating it to some expression. |
| − | + | # Give a sentence like the following: "At <math>x=c</math>, the function <math>f</math> is..." | |
| − | + | # Evaluate the function. | |
| − | + | ||
| − | + | === Description === | |
| − | + | There are many ways which people describe functions. In the examples above, a verbal descriptions is given (the height of the ball above the earth as a function of time). Here is a list of ways to describe functions. The top three listed approaches to describing functions are the most popular. | |
| − | < | + | |
| − | + | # A function is given a name (such as <math>f</math>) and a formula for the function is also given. For example, <math>f(x)=3x+2</math> describes a function. We refer to the input as the '''argument''' of the function (or the '''independent variable'''), and to the output as the '''value''' of the function at the given argument. | |
| − | + | # A function is described using an equation and two variables. One variable is for the input of the function and one is for the output of the function. The variable for the input is called the '''independent variable'''. The variable for the output is called the '''dependent variable'''. For example, <math>y=3x+2</math> describes a function. The dependent variable appears by itself on the left hand side of equal sign. | |
| − | + | # A verbal description of the function. | |
| − | + | ||
| − | + | When a function is given a name (like in number 1 above), the name of the function is usually a single letter of the alphabet (such as <math>f</math> or <math>g</math>). Some functions whose names are multiple letters (like the sine function <math>y=\sin(x)</math> | |
| − | + | ||
| + | ===Plugging a value into a function=== | ||
| + | If we write <math>f(x)=3x+2</math> , then we know that | ||
| + | |||
| + | *The function <math>f</math> is a function of <math>x</math> . | ||
| + | *To evaluate the function at a certain number, replace the <math>x</math> with that number. | ||
| + | *Replacing <math>x</math> with that number in the right side of the function will produce the function's output for that certain input. | ||
| + | *In English, the definition of <math>f</math> is interpreted, "Given a number, <math>f</math> will return ''two more than the triple of that number''." | ||
| + | |||
| + | How would we know the value of the function <math>f</math> at 3? | ||
| + | We would have the following three thoughts: | ||
| + | |||
| + | # <math>f(3)=3(3)+2</math> | ||
| + | # <math>3(3)+2=9+2</math> | ||
| + | # <math>9+2=11</math> | ||
| + | and we would write | ||
| + | |||
| + | <math>f(3)=3(3)+2=9+2=11</math>. | ||
| + | |||
| + | The value of <math>f</math> at 3 is 11. | ||
| + | |||
| + | Note that <math>f(3)</math> means the value of the dependent variable when <math>x</math> takes on the value of 3. So we see that the number ''11'' is the output of the function when we give the number ''3'' as the input. People often summarize the work above by writing "the value of <math>f</math> at three is eleven", or simply "<math>f</math> of three equals eleven". | ||
| + | |||
| + | ==Basic concepts of functions== | ||
| + | The formal definition of a function states that a function is actually a ''mapping'' that associates the elements of one set called the '''domain''' of the function, <math>A</math>, with the elements of another set called the ''range'' of the function, <math>B</math>. For each value we select from the domain of the function, there exists ''exactly one'' corresponding element in the range of the function. The definition of the function tells us which element in the range corresponds to the element we picked from the domain. An example of how is given below. | ||
| + | |||
| + | ===Example=== | ||
| + | Let function <math>f(x)=5x+\frac{5x}{2}</math> for all <math>x</math>. For what value of <math>x</math> gives <math>f(x)=225\frac{1}{2}</math> | ||
| + | In mathematics, it is important to notice any repetition. If something seems to repeat, keep a note of that in the back of your mind somewhere. | ||
| − | + | Here, notice that <math>f(x)=5x+\frac{5x}{2}</math> and <math>f(x)=225\frac{1}{2}</math>. Because <math>f(x)</math> is equal to two different things, it must be the case that the other side of the equal sign to <math>f(x)</math> is equal to the other. This property is known as the transitive property and could thus make the following equation below true:<br> | |
| + | :<math>225\frac{1}{2}=5x+\frac{5x}{2}</math> | ||
| − | In | + | Next, simplify — make your life easier rather than harder. In this instance, since <math>5x+\frac{5x}{2}</math> has <math>x</math> as a like-term, and the two terms are fractions added to the other, put it over a common denominator and simplify. Similar, since <math>225\frac{1}{2}</math> is a mixed fraction, <math>225\frac{1}{2}=225+\frac{1}{2}</math>.<br> |
| + | :<math>225\frac{1}{2}=5x+\frac{5x}{2}</math><br> | ||
| + | :<math>\Rightarrow\frac{225}{1}+\frac{1}{2}=\frac{5x}{1}+\frac{5x}{2}</math><br> | ||
| + | :<math>\Rightarrow\frac{450}{2}+\frac{1}{2}=\frac{10x}{2}+\frac{5x}{2}</math><br> | ||
| + | :<math>\Rightarrow\frac{451}{2}=\frac{15x}{2}</math> | ||
| − | + | Multiply both sides by the reciprocal of the coefficient of <math>x</math>, <math>\frac{2}{15}</math> from both sides by multiplying by it.<br> | |
| + | :<math>\frac{2}{15}\cdot\frac{451}{2}=x</math><br> | ||
| + | :<math>\frac{451}{15}=x</math> ''or'' <math>x=\frac{451}{15}</math>. | ||
| − | The | + | The value of <math>x</math> that makes <math>f(x)=225\frac{1}{2}</math> is <math>x=\frac{451}{15}</math>. |
| − | + | Classically, the element picked from the domain is pictured as something that is fed into the function and the corresponding element in the range is pictured as the output. Since we "pick" the element in the domain whose corresponding element in the range we want to find, we have control over what element we pick and hence this element is also known as the "independent variable". The element mapped in the range is beyond our control and is "mapped to" by the function. This element is hence also known as the "dependent variable", for it depends on which independent variable we pick. Since the elementary idea of functions is better understood from the classical viewpoint, we shall use it hereafter. However, it is still important to remember the correct definition of functions at all times. | |
| − | === | + | === Basic types of transformation === |
| − | + | To make it simple, for the function <math>f(x)</math>, all of the possible <math>x</math> values constitute the domain, and all of the values <math>f(x)</math> (<math>y</math> on the x-y plane) constitute the range. To put it in more formal terms, a function <math>f</math> is a mapping of some element <math>a\in A</math>, called the domain, to exactly one element <math>b\in B</math>, called the range, such that <math>f:A\to B</math>. The image below should help explain the modern definition of a function: | |
| + | [[File:Function_Definition.svg|alt=The image demonstrates a mapping of some element a (the circle) in A, the domain, to exactly one element b in B, the range.|thumb|<math>A</math> is the domain of the function while <math>B</math> is the range. This transformation from set <math>A</math> to <math>B</math> is an example of one-to-one function.]] | ||
| + | # A function is considered '''one-to-one''' if an element <math>a\in A</math> from domain <math>A</math> of function <math>f</math>, leads to exactly one element <math>b\in B</math> from range <math>B</math> of the function. By definition, since only one element <math>b</math> is mapped by function <math>f</math> from some element <math>a</math>, <math>f:A\to B</math> implies that there exists only one element <math>b</math> from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to '''''Figure 1'''''. | ||
| + | # A function is considered '''many-to-one''' if some elements <math>a_{1},a_{2},\ldots a_{n}\in A</math> from domain <math>A</math> of function <math>f</math> maps to exactly one element <math>b\in B</math> from range <math>B</math> of the function. Since some elements <math>\left( a_{1},a_{2},\ldots a_{n} \right)\in A</math> must map onto exactly one element <math>b\in B</math>, <math>f:A\to B</math> must be compliant with the definition of a function. Therefore, there exists a many-to-one function. | ||
| + | # A function is considered '''one-to-many''' if exactly one element <math>a\in A</math> from domain <math>A</math> of function <math>f</math> maps to some elements <math>\left( b_{1},b_{2},\ldots b_{n} \right)\in B</math> from range <math>B</math> of the function. If some element <math>a</math> maps onto many distinct elements <math>b</math>, then <math>f:A\to B</math> is non-functional since there exists many distinct elements <math>b</math>. Given many-to-one is non-compliant to the definition of a function, there exists no function that is one-to-many. | ||
| − | + | The modern definition describes a function sufficiently such that it helps us determine whether some new type of "function" is indeed one. Now that each case is defined above, you can now prove whether functions are one of these function cases. Here is an example problem: | |
| − | |||
| − | + | ===One-to-One Example=== | |
| − | : <math> | + | '''Given''': <math>f(x)=ax+b</math>, where <math>a</math> and <math>b</math> are constant and <math>a\ne0</math>.<br> |
| + | '''Prove''': function <math>f</math> is one-to-one.}} Notice that the only changing element in the function <math>f</math> is <math>x</math>. To prove a function is one-to-one by applying the definition may be impossible because although two random elements of domain set <math>A</math> may not be many-to-one, there may be some elements <math>\left( a_{1},a_{2},\ldots a_{n} \right)\in A</math> that may make the function many-to-one. To account for this possibility, we must prove that it is impossible to have some result like that. | ||
| − | + | Assume there exists two distinct elements <math>x_{1}\ne x_2</math> that will result in <math>f\left( x_{1} \right) =f\left( x_{2} \right)</math>. This would make the function many-to-one. In consequence,<br> | |
| + | <math display="block">ax_{1}+b=ax_{2}+b</math> | ||
| − | + | Subtract <math>b</math> from both sides of the equation. | |
| + | :<math>\Rightarrow ax_{1}=ax_{2}</math> | ||
| − | + | Subtract <math>ax_{2}</math> from both sides of the equation. | |
| + | :<math>\Rightarrow ax_{1}-ax_{2}=0</math> | ||
| − | + | Factor <math>a</math> from both terms to the left of the equation. | |
| − | + | :<math>\Rightarrow a\left( x_{1}-x_{2} \right) =0</math> | |
| − | :<math> | ||
| − | + | Multiply <math>\frac{1}{a}</math> to both sides of the equation. | |
| + | :<math>\Rightarrow \left( x_{1}-x_{2} \right) =0</math> | ||
| − | + | Add <math>x_{2}</math> to both sides of the equation. | |
| + | :<math>\Rightarrow x_{1}=x_{2}</math> | ||
| − | = | + | Notice that <math>x_{1}=x_{2}</math>. However, this is impossible because <math>x_{1}</math> and <math>x_{2}</math> are distinct. Ergo, <math>f\left( x_{1} \right)\ne f\left( x_{2} \right)</math>. No two distinct inputs can give the same output. Therefore, the function must be one-to-one. |
| − | + | === Basic concepts === | |
| + | [[File:Domain, Range, Codomain.svg|thumb|230x230px|The domain is all the elements in set <math>A</math> that can be mapped to the elements in set <math>B</math>. | ||
| − | + | The range is those elements in set <math>B</math> which are mapped with the domain. | |
| − | + | The codomain is all the elements in set <math>B</math>.]]There are a few more important ideas to learn from the modern definition of the function, and it comes from knowing the difference between domain, range, and codomain. We already discussed some of these, yet knowing about sets adds a new definition for each of the following ideas. Therefore, let us discuss these based on these new ideas. Let <math>A</math> and <math>B</math> be a set. If we were to combine these two sets, it would be defined as the ''cartesian cross product'' <math>A\times B</math>. The subset of this product is the function. The below definitions are a little confusing. The best way to interpret these is to draw an image. To the right of these definitions is the image that corresponds to it. | |
| − | |||
| − | + | ====Definition of domain, range, and codomain of a function==== | |
| − | |||
| − | |||
| − | |||
| − | + | The '''domain''' is defined to be a set <math>A</math> | |
| + | with all elements <math>a\in A</math> mapping to at least one unique <math>b\in B</math> . | ||
| − | :<math> | + | The set of elements in <math>B</math> is the '''range''' of the function mapping <math>f:A\to B</math> in the cartesian cross product, whereby the set of all elements <math>a\in A</math> maps to some element <math>b\in B</math> . |
| − | + | The '''codomain''' is the set <math>B</math>, where it is not necessarily the case that all elements <math>b\in B</math> was mapped by some <math>a\in A</math>. | |
| − | + | Note that the codomain is not as important as the other two concepts. | |
| − | = | + | Take <math>f(x)=\sqrt{1-x^2}</math> for example:[[Image:Domainofsemicirclefunction.png|thumb|The domain of the function is the interval from -1 to 1]]Because of the square root, the content in the square root should be strictly not smaller than 0.<blockquote><math>1-x^2\geq0</math></blockquote><blockquote><math>\Leftrightarrow -1\leq x\leq 1</math></blockquote>Thus the domain is<blockquote><math>x\in[-1,1]</math></blockquote>[[Image:Rangeofsemicirclefunction.png|thumb|The range of the function is the interval from 0 to 1]] |
| − | |||
| − | + | Correspondingly, the range will be<blockquote><math>f(x)\in[0,1]</math></blockquote> | |
| − | |||
| − | |||
| − | + | === Other types of transformation === | |
| − | + | There is one more final aspect that needs to be defined. We already have a good idea of what makes a mapping a function (e.g. it cannot be one-to-many). However, three more definitions that you will often hear will be necessary to talk about: ''injective'', ''surjective'', ''bijective''. | |
| + | [[File:Injective, Surjective, Bijective.svg|488x488px|alt=|none|thumb|The function mapping on the left is an example of an injective function because it is one-to-one. However, it is not surjective because the range and the codomain are not the same.]] | ||
| − | + | * A function is '''injective''' if it is one-to-one. | |
| − | + | * A function is '''surjective''' if it is "onto." That is, the mapping <math>f:A\to B</math> has <math>B</math> as the ''range'' of the function, where the codomain and the range of the function are the same. | |
| − | + | * A function is '''bijective''' if it is both surjective and injective. | |
| − | |||
| − | the | + | Again, the above definitions are often very confusing. Again, another image is provided to the right of the bullet points. Along with that, another example is also provided. Let us analyze the function <math>g(x)=ax^{2}</math>. |
| − | |||
| − | + | '''Given''': <math>g(x)=ax^{2}</math>, where <math>a</math> is constant and <math>a\ne0</math>.<br> | |
| + | '''Prove''': function <math>g</math> is non-surjective and non-injective. | ||
| − | + | Notice that the only changing element in the function <math>g</math> is <math>x</math>. Let us check to see the conditions of this function. | |
| − | + | '''Is it injective'''? Let <math>g(x)=y</math>, and solve for <math>x</math>. First, divide by <math>a</math>. | |
| + | :<math>y=ax^{2}</math> | ||
| + | :<math>\Rightarrow \frac{y}{a}=x^{2}</math> | ||
| − | + | Then take the square root of <math>x^2</math>. By definition, <math>\sqrt{x^{2}}=\pm\sqrt{x^{2}}=\pm x</math>, so | |
| + | :<math>\frac{y}{a}=x^{2}</math> | ||
| + | :<math>\Rightarrow\pm\sqrt{\frac{y}{a}}=\pm x</math> | ||
| − | + | Notice, however, what we learned from the above manipulation. As a result of solving for <math>x</math>, we found that there are two solutions for <math>x</math>. However, this resulted in two different values from <math>\frac{y}{a}</math>. This means that for some individual <math>x</math> that gives <math>y</math>, there are two different inputs that result in the same value. Because <math>f(x_{1})=f(x_{2})</math> when <math>x_{1}\ne x_{2}</math>, this is by definition non-injective. | |
| − | === | + | '''Is it surjective'''? As a natural consequence of what we learned about inputs, let us determine the range of the function. After all, the only way to determine if something is surjective is to see if the range applies to all real numbers. A good way to determine this is by finding a pattern involving our domains. Let us say we input a negative number for the domain: <math>f(-x)=a(-x)^{2}=a\cdot(-x)\cdot(-x)=ax^2</math>. This seemingly trivial exercise tells us that negative numbers give us non-negative numbers for our range. This is huge information! For <math>x\in\mathbb{R}</math>, the function always results <math>y>0</math> for our range. For the set <math>B</math>, we have elements in that set that have no mappings from the set <math>A</math>. As such, <math>y\le0</math> is the codomain of set <math>B</math>. Therefore, this function is non-surjective! |
| + | [[Image:Vertlinetest.png|thumb|This is an example of an expression which fails the vertical line test.]] | ||
| − | + | === Tests for equations === | |
| − | |||
| − | |||
| − | + | ====The vertical line test==== | |
| + | The vertical line test is a systematic test to find out if an equation involving <math>x</math> and <math>y</math> can serve as a function (with <math>x</math> the independent variable and <math>y</math> the dependent variable). Simply graph the equation and draw a vertical line through each point of the <math>x</math>-axis. If any vertical line ever touches the graph at more than one point, then the equation is not a function; if the line always touches at most one point of the graph, then the equation is a function. | ||
| − | + | The circle, on the right, is not a function because the vertical line intercepts two points on the graph when <math>x=1</math>. | |
| − | |||
| − | == | + | ==== The horizontal line and the algebraic 1-1 test ==== |
| − | + | Similarly, the horizontal line test, though does not test if an equation is a function, tests if a function is injective (one-to-one). If any horizontal line ever touches the graph at more than one point, then the function is not one-to-one; if the line always touches at most one point on the graph, then the function is one-to-one. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The algebraic 1-1 test is the non-geometric way to see if a function is one-to-one. The basic concept is that: | |
| − | |||
| − | + | Assume there is a function <math>f</math>. If:<blockquote><math>f(a)=f(b)</math>, and <math>a=b</math>, then</blockquote>function <math>f</math> is one-to-one. | |
| − | + | Here is an example: prove that <math>f(x)=\frac{1-2x}{1+x}</math> is injective. | |
| − | + | Since the notation is the notation for a function, the equation is a function. So we only need to prove that it is injective. Let <math>a</math> and <math>b</math> be the inputs of the function and that <math>f(a)=f(b)</math>. Thus, | |
| − | + | :<math>\frac{1-2a}{1+a}=\frac{1-2b}{1+b}</math> | |
| − | + | :<math>\Leftrightarrow(1+b)(1-2a)=(1+a)(1-2b)</math> | |
| + | :<math>\Leftrightarrow1-2a+b-2ab=1-2b+a-2ab</math><br><math>\Leftrightarrow1-2a+b=1-2b+a</math> | ||
| + | :<math>\Leftrightarrow1-2a+3b=1+a</math> | ||
| + | :<math>\Leftrightarrow1+3b=1+3a</math> | ||
| + | :<math>\Leftrightarrow a=b</math> | ||
| − | + | So, the result is <math>a=b</math>, proving that the function is injective. | |
| − | |||
| − | + | Another example is proving that <math>g(x)=x^2</math> is not injective. | |
| − | |||
| − | |||
| − | + | Using the same method, one can find that <math>a=\pm b</math>, which is not <math>a=b</math>. So, the function is not injective. | |
| − | + | ===Remarks=== | |
| + | The following arise as a direct consequence of the definition of functions: | ||
| + | #By definition, for each "input" a function returns only one "output", corresponding to that input. While the same output may correspond to more than one input, one input cannot correspond to more than one output. This is expressed graphically as the ''vertical line test'': a line drawn parallel to the axis of the dependent variable (normally vertical) will intersect the graph of a function only once. However, a line drawn parallel to the axis of the independent variable (normally horizontal) may intersect the graph of a function as many times as it likes. Equivalently, this has an algebraic (or formula-based) interpretation. We can always say if <math>a=b</math> , then <math>f(a)=f(b)</math> , but if we only know that <math>f(a)=f(b)</math> then we can't be sure that <math>a=b</math> . | ||
| + | #Each function has a set of values, the function's ''domain'', which it can accept as input. Perhaps this set is all positive real numbers; perhaps it is the set {pork, mutton, beef}. This set must be implicitly/explicitly defined in the definition of the function. You cannot feed the function an element that isn't in the domain, as the function is not defined for that input element. | ||
| + | #Each function has a set of values, the function's ''range'', which it can output. This may be the set of real numbers. It may be the set of positive integers or even the set {0,1}. This set, too, must be implicitly/explicitly defined in the definition of the function. | ||
| + | Functions are an important foundation of mathematics. This modern interpretation is a result of the hard work of the mathematicians of history. It was not until recently that the definition of the relation was introduced by René Descartes in ''Geometry'' (1637). Nearly a century later, the standard notation (<math>f(x)=y</math>) was first introduced by Leonhard Euler in ''Introductio in Analysin Infinitorum'' and ''Institutiones Calculi Differentialis''. The term function was also a new innovation during Euler's time as well, being introduced Gottfried Wilhelm Leibniz in a 1673 letter "to describe a quantity related to points of a curve, such as a coordinate or curve's slope." Finally, the modern definition of the function being the relation among sets was first introduced in 1908 by Godfrey Harold Hardy where there is a relation between two variables <math>x</math> and <math>y</math> such that "to some values of <math>x</math> at any rate correspond values of <math>y</math>." | ||
| − | + | ==Important functions== | |
| − | + | === Polynomials === | |
| − | + | Polynomial functions are the most common and most convenient functions in the world of calculus. Their frequent appearances and their applications on computer calculations have made them important. | |
| − | + | A polynomial in a single indeterminate x can always be written (or rewritten) in the form: | |
| − | |||
| − | |||
| − | + | :<math>f(x)=a_n x^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdot\cdot\cdot+a_2x^2+a_1x+a_0</math> | |
| − | |||
| − | + | To be more concise, it can also be written in the summation form: | |
| + | :<math>\sum_{k=0}^n a_k x^k</math> | ||
| − | + | ==== Constant ==== | |
| + | [[File:Linear Function Graph Orthogonal.svg|thumb|Two linear functions are shown on the image. One is <math>f(x)=\frac{1}{2}x+2</math> and the other is <math>g(x)=-2x+5 </math>]] | ||
| + | When <math>n=0</math>, the polynomial can be rewritten into the following function:<blockquote><math>f(x)=C</math>, where <math>C</math> is a constant.</blockquote>The graph of this function is a horizontal line passing the point <math>(0,C)</math>. | ||
| − | + | ==== Linear ==== | |
| + | When <math>n=1</math>, the polynomial can be rewritten into<blockquote><math>f(x)=mx+b</math>, where <math>m\text{ and }b</math> are constants.</blockquote>The graph of this function is a straight line passing the point <math>(0,b)</math> and <math>(-\frac{b}{m},0)</math>, and the slope of this function is <math>m</math>. | ||
| + | [[File:Qfunction.png|thumb|right|This is the graph of a quadratic function.]] | ||
| − | + | ==== Quadratic ==== | |
| + | When <math>n=2</math>, the polynomial can be rewritten into<blockquote><math>f(x)=ax^2+bx+c</math>, where <math>a,b,c</math> are constants.</blockquote>The graph of this function is a parabola, like the trajectory of a basketball thrown into the hoop. | ||
| − | + | If there are questions about the quadratic formula and other basic polynomial concepts, please review the respective chapters in Algebra. | |
| − | === | + | === Trigonometric === |
| + | Trigonometric functions are also very important because it can connect algebra and geometry. Trigonometric functions are explained in detail here due to its importance and difficulty.[[File:Logexponential.png|thumb|right|The curve on the left is an exponential function while the curve on the right is a logarithmic one|256x256px]] | ||
| + | === Exponential and Logarithmic === | ||
| + | Exponential and logarithmic functions have a unique identity when calculating the derivatives, so this is a great time to review those functions. | ||
| + | The exponential function is defined as: | ||
| + | :<math>f(x)=a^x</math>, where <math>a</math> is a constant. | ||
| + | while the logarithmic function is defined as: | ||
| + | :<math>f(x)=\log_b x</math>, where <math>b</math> is a constant. | ||
| + | A special number will be frequently seen in those functions: the Euler's constant, also known as the base of the natural logarithm. Notated as <math>e</math>, it is defined as <math>e=\sum_{n=0}^\infty \frac{1}{n!}</math>. | ||
| − | + | === Signum === | |
| + | The Signum (sign) function is simply defined as<blockquote><math>\mbox{sgn}(x)=\left\{\begin{matrix}-1 & \text{if} & x<0\\0 & \text{if} & x=0 \\ 1 & \text{if} & x>0 \end{matrix} \right.</math></blockquote> | ||
| − | + | == Properties of functions == | |
| + | Sometimes, a lot of function manipulations cannot be achieved without some help from basic properties of functions. | ||
| − | + | === Domain and range === | |
| + | This concept is discussed above. | ||
| − | === | + | === Growth === |
| − | + | Although it seems obvious to spot a function increasing or decreasing, without the help of graphing software, we need a mathematical way to spot whether the function is increasing or decreasing, or else our human minds cannot immediately comprehend the huge amount of information. | |
| − | |||
| − | + | Assume a function <math>f(x)</math> with inputs <math>x_1,x_2</math>, and that <math>x_1\in[a,b]</math>, <math>x_2\in[a,b]</math>, and <math>x_2>x_1</math> at all times.<blockquote>If for all <math>x_1</math> and <math>x_2</math>, <math>f(x_2)-f(x_1)>0</math>, then | |
| − | |||
| − | and | ||
| − | |||
| − | + | <math>f(x)</math> is increasing in <math>[a,b]</math> | |
| − | + | If for all <math>x_1</math> and <math>x_2</math>, <math>f(x_2)-f(x_1)<0</math>, then | |
| − | = | + | <math>f(x)</math> is decreasing in <math>[a,b]</math></blockquote>'''Example:''' In which intervals is <math>f(x)=\frac{1}{1-x^2}</math> increasing? |
| − | {{ | ||
| − | |||
| − | |||
| − | + | Firstly, the domain is important. Because the denominator cannot be 0, the domain for this function is | |
| − | + | <math>x\in(-\infty,-1)\cup(-1,1)\cup(1,\infty)</math> | |
| − | In | + | In <math>(-\infty,-1)</math>, the growth of the function is:<blockquote>Let <math>x_1,x_2\in[-\infty,-1]</math> and <math>x_2>x_1</math> |
| − | + | Thus,<blockquote><math>f(x_2)-f(x_1)=\frac{1}{1-x_2^2}-\frac{1}{1-x_1^2}=\frac{x_2^2-x_1^2}{(1-x_2^2)(1-x_1^2)}</math></blockquote><math>\because</math> both <math>x_1,x_2\in[-\infty,-1]</math> | |
| − | + | <math>\therefore</math> <math>(1-x_2^2)(1-x_1^2)>0</math> | |
| − | + | <math>\because</math> <math>x_2>x_1</math> and <math>x_1<x_2<0</math> | |
| − | |||
| − | |||
| − | { | + | <math>\therefore</math> <math>x_2^2-x_1^2<0</math><blockquote>So, <math>f(x_2)-f(x_1)=\frac{x_2^2-x_1^2}{(1-x_2^2)(1-x_1^2)}<0</math></blockquote><math>f(x)</math> is decreasing in <math>(-\infty,-1)</math></blockquote>In <math>(-1,1)</math><blockquote>Let <math>x_1,x_2\in[-1,1]</math> and <math>x_2>x_1</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Thus,<blockquote><math>f(x_2)-f(x_1)=\frac{1}{1-x_2^2}-\frac{1}{1-x_1^2}=\frac{x_2^2-x_1^2}{(1-x_2^2)(1-x_1^2)}</math></blockquote><math>\because</math> both <math>x_1,x_2\in[-\infty,-1]</math> | |
| − | + | <math>\therefore</math><math>(1-x_2^2)(1-x_1^2)>0</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | However, the sign of <math>x_2^2-x_1^2</math> in <math>(-1,1)</math> cannot be determined. It can only be determined in <math>(-1,0)\text{ and }(0,1)</math>.<blockquote>In <math>(-1,0)</math> | |
| − | + | <math>\because</math> <math>x_2>x_1</math> and <math>x_1<x_2<0</math> | |
| − | |||
| − | |||
| − | + | <math>\therefore</math> <math>x_2^2-x_1^2<0</math> | |
| − | + | In <math>(0,1)</math> | |
| − | + | <math>\because x_2>x_1\text{ and }0<x_1<x_2</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>\therefore x_2^2-x_1^2>0</math></blockquote>As a result, | |
| − | |||
| − | + | <math>f(x)</math> is decreasing in <math>(-1,0)</math> and increasing in <math>(0,1)</math>.</blockquote>In <math>(1,\infty)</math><blockquote>Let <math>x_1,x_2\in[1,\infty]</math> and <math>x_2>x_1</math> | |
| − | |||
| − | + | Thus,<blockquote><math>f(x_2)-f(x_1)=\frac{1}{1-x_2^2}-\frac{1}{1-x_1^2}=\frac{x_2^2-x_1^2}{(1-x_2^2)(1-x_1^2)}</math></blockquote><math>\because</math> both <math>x_1,x_2\in[-\infty,-1]</math> | |
| − | + | <math>\therefore</math><math>(1-x_2^2)(1-x_1^2)>0</math> | |
| − | + | <math>\because x_2>x_1\text{ and }0<x_1<x_2</math> | |
| − | |||
| − | + | <math>\therefore x_2^2-x_1^2>0</math><blockquote>So, <math>f(x_2)-f(x_1)=\frac{x_2^2-x_1^2}{(1-x_2^2)(1-x_1^2)}>0</math></blockquote><math>f(x)</math> is increasing in <math>(1,\infty)</math>.</blockquote>Therefore, the intervals in which the function is increasing are <math>(0,1)\And(1,\infty)</math>. | |
| − | <math> | ||
| − | < | + | <math>\blacksquare</math> |
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | After learning derivatives, there will be more ways to determine the growth of a function. | |
| − | |||
| − | |||
| − | |||
| − | The | + | === Parity === |
| + | The properties odd and even are associated with symmetry. While even functions have a symmetry about the <math>y</math>-axis, odd functions are symmetric about the origin. In mathematical terms:<blockquote>A function is even when <math>f(-x)=f(x)</math> | ||
| − | + | A function is odd when <math>f(-x)=-f(x)</math></blockquote>'''Example:''' Prove that <math>f(x)=\frac{1}{1-x^2}</math> is an even function. | |
| − | :<math>f | ||
| − | |||
| − | + | <math>\because f(-x)=\frac{1}{1-(-x)^2}=\frac{1}{1-x^2}=f(x)</math> | |
| − | + | <math>\therefore f(x) </math> is an even function | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Manipulating functions== | |
| + | ===Addition, Subtraction, Multiplication and Division of functions=== | ||
| + | For two real-valued functions, we can add the functions, multiply the functions, | ||
| + | raised to a power, etc. For example: | ||
| − | == | + | * If we add the functions <math>y=3x+2</math> and <math>y=x^2</math> , we obtain <math>y=x^2+3x+2</math> . |
| − | |||
| − | |||
| − | + | * If we subtract <math>y=3x+2</math> from <math>y=x^2</math> , we obtain <math>y=x^2-(3x+2)</math> . We can also write this as <math>y=x^2-3x-2</math> . | |
| − | + | * If we multiply the function <math>y=3x+2</math> and the function <math>y=x^2</math> , we obtain <math>y=(3x+2)x^2</math> . We can also write this as <math>y=3x^3+2x^2</math> . | |
| − | + | * If we divide the function <math>y=3x+2</math> by the function <math>y=x^2</math> , we obtain <math>y=\frac{3x+2}{x^2}</math> . | |
| − | + | If a math problem wants you to add two functions <math>f</math> and <math>g</math> , there are two ways that the problem will likely be worded: | |
| − | + | #If you are told that <math>f(x)=3x+2</math> , that <math>g(x)=x^2</math> , that <math>h(x)=f(x)+g(x)</math> and asked about <math>h</math> , then you are being asked to add two functions. Your answer would be <math>h(x)=x^2+3x+2</math> . | |
| + | #If you are told that <math>f(x)=3x+2</math> , that <math>g(x)=x^2</math> and you are asked about <math>f+g</math> , then you are being asked to add two functions. The addition of <math>f</math> and <math>g</math> is called <math>f+g</math> . Your answer would be <math>(f+g)(x)=x^2+3x+2</math> . | ||
| − | + | Similar statements can be made for subtraction, multiplication and division. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let <math>f(x)=3x+2</math> and: <math>g(x)=x^2</math> . Let's add, subtract, multiply and divide. | |
| − | + | :<math>\begin{align} | |
| + | (f+g)(x) | ||
| + | &= f(x)+g(x)\\ | ||
| + | &= (3x+2)+(x^2)\\ | ||
| + | &= x^2+3x+2\, | ||
| + | \end{align}</math> , | ||
| − | |||
| − | + | :<math>\begin{align} | |
| − | + | (f-g)(x) | |
| − | + | &= f(x)-g(x)\\ | |
| + | &= (3x+2)-(x^2)\\ | ||
| + | &= -x^2+3x+2\, | ||
| + | \end{align}</math> , | ||
| − | |||
| − | |||
| − | + | :<math>\begin{align} | |
| − | + | (f\times g)(x) | |
| − | + | &= f(x)\times g(x)\\ | |
| − | + | &= (3x+2)\times(x^2)\\ | |
| − | + | &= 3x^3+2x^2\, | |
| + | \end{align}</math> , | ||
| − | |||
| − | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | + | \left(\frac{f}{g}\right)(x) | |
| − | + | &= \frac{f(x)}{g(x)}\\ | |
| − | + | &= \frac{3x+2}{x^2}\\ | |
| − | + | &= \frac{3}{x}+\frac{2}{x^2} | |
| + | \end{align}</math> . | ||
| + | |||
| + | ===Composition of functions=== | ||
| + | We begin with a fun (and not too complicated) application of composition of functions before we talk about what composition of functions is. | ||
| − | == | + | Example: Dropping a ball |
| + | If we drop a ball from a bridge which is 20 meters above the ground, then the height of our ball above the earth is a function of time. The physicists tell us that if we measure time in seconds and distance in meters, then the formula for height in terms of time is <math>h=-4.9t^2+20</math> . Suppose we are tracking the ball with a camera and always want the ball to be in the center of our picture. Suppose we have <math>\theta=f(h)</math> The angle will depend upon the height of the ball above the ground and the height above the ground depends upon time. So the angle will depend upon time. This can be written as <math>\theta=f(-4.9t^2+20)</math> . We replace <math>h</math> with what it is equal to. This is the essence of composition. | ||
| − | + | Composition of functions is another way to combine functions which is different from addition, | |
| + | subtraction, multiplication or division. | ||
| − | + | The value of a function <math>f</math> depends upon the value of another variable <math>x</math> ; however, that variable could be equal to another function <math>g</math> , so its value depends on the value of a third variable. If this is the case, then the first variable is a function <math>h</math> of the third variable; this function (<math>h</math>) is called the '''composition''' of the other two functions (<math>f</math> and <math>g</math>). | |
| − | + | Example: Composing two functions | |
| − | + | Let <math>f(x)=3x+2</math> and: <math>g(x)=x^2</math> . The composition of <math>f</math> with <math>g</math> is read as either "f composed with g" or "f of g of x." | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let | |
| + | :<math>h(x)=f(g(x))</math> | ||
| + | Then | ||
| − | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | + | h(x) &= f(g(x))\\ | |
| − | + | &= f(x^2)\\ | |
| − | + | &= 3(x^2)+2\\ | |
| − | \end{align} | + | &= 3x^2+2\, |
| − | + | \end{align}</math> . | |
| − | |||
| − | |||
| − | + | Sometimes a math problem asks you compute <math>(f\circ g)(x)</math> | |
| + | when they want you to compute <math>f(g(x))</math> , | ||
| − | + | Here, <math>h</math> is the composition of <math>f</math> and <math>g</math> and we write <math>h=f\circ g</math> . Note that composition is not commutative: | |
| − | + | :<math>f(g(x))=3x^2+2</math> , and | |
| − | + | :<math>\begin{align} | |
| − | :<math> | + | g(f(x)) &= g(3x+2)\\ |
| − | + | &= (3x+2)^2\\ | |
| − | + | &= 9x^2+12x+4\, . | |
| + | \end{align}</math> | ||
| − | + | :so <math>f(g(x))\ne g(f(x))</math> . | |
| − | |||
| − | + | Composition of functions is very common, mainly because functions themselves are common. For instance, squaring and sine are both functions: | |
| − | + | :<math>\mbox{square}(x)=x^2</math> | |
| − | + | :<math>\mbox{sine}(x)=\sin(x)</math> | |
| − | { | ||
| − | |||
| − | + | Thus, the expression <math>\sin^2(x)</math> is a composition of functions: | |
| + | :{| | ||
| + | |- | ||
| + | | <math>\sin^2(x)</math> | ||
| + | | <math>=\mbox{square}(\sin(x))</math> | ||
| + | |- | ||
| + | | | ||
| + | | <math>=\mbox{square}(\mbox{sine}(x))</math> | ||
| + | |} | ||
| + | |||
| + | (Note that this is ''not'' the same as <math>\mbox{sine}(\mbox{square}(x))=\sin(x^2)</math>.) | ||
| + | Since the function sine equals <math>\tfrac{1}{2}</math> if <math>x=\frac{\pi}{6}</math> , | ||
| + | |||
| + | :<math>\mbox{square}\left(\sin\left(\tfrac{\pi}{6}\right)\right)=\mbox{square}\left(\tfrac{1}{2}\right)</math> . | ||
| + | |||
| + | Since the function square equals <math>\frac{1}{4}</math> if <math>x=\frac{\pi}{6}</math> , | ||
| − | = | + | :<math>\sin^2\left(\tfrac{\pi}{6}\right)=\mbox{square}\left(\sin\left(\tfrac{\pi}{6}\right)\right)=\mbox{square}\left(\tfrac{1}{2}\right)=\frac{1}{4}</math> . |
| − | {{ | ||
| − | |||
| − | |||
| − | |||
| − | + | ===Transformations=== | |
| + | Transformations are a type of function manipulation that are very common. They consist of multiplying, dividing, adding or subtracting constants to either the input or the output. Multiplying by a constant is called '''dilation''' and adding a constant is called '''translation'''. Here are a few examples: | ||
| − | + | :<math>f(2\times x)</math> Dilation | |
| + | :<math>f(x+2)</math> Translation | ||
| + | :<math>2\times f(x)</math> Dilation | ||
| + | :<math>2+f(x)</math> Translation | ||
| − | + | [[image:4_function_translations.jpg|right|thumb|250px|Examples of horizontal and vertical translations]] | |
| + | [[image:4_function_dilations.jpg|right|thumb|250px|Examples of horizontal and vertical dilations]] | ||
| + | Translations and dilations can be either horizontal or vertical. Examples of both vertical and horizontal translations can be seen at right. The red graphs represent functions in their 'original' state, the solid blue graphs have been translated (shifted) horizontally, and the dashed graphs have been translated vertically. | ||
| − | + | Dilations are demonstrated in a similar fashion. The function | |
| + | :<math>f(2\times x)</math> | ||
| + | has had its input doubled. One way to think about this is that now any change in the input will be doubled. If I add one to <math>x</math>, I add two to the input of <math>f</math>, so it will now change twice as quickly. Thus, this is a horizontal dilation by <math>\frac{1}{2}</math> because the distance to the <math>y</math>-axis has been '''halved'''. A vertical dilation, such as | ||
| + | :<math>2\times f(x)</math> | ||
| + | is slightly more straightforward. In this case, you double the output of the function. The output represents the distance from the <math>x</math>-axis, so in effect, you have made the graph of the function 'taller'. Here are a few basic examples where <math>a</math> is any positive constant: | ||
| − | + | {| cellpadding="10" border="1" | |
| + | |- | ||
| + | |Original graph | ||
| + | |<math>f(x)</math> | ||
| + | |Rotation about origin | ||
| + | |<math>-f(-x)</math> | ||
| + | |- | ||
| + | |Horizontal translation by <math>a</math> units '''left''' | ||
| + | |<math>f(x+a)</math> | ||
| + | |Horizontal translation by <math>a</math> units '''right''' | ||
| + | |<math>f(x-a)</math> | ||
| + | |- | ||
| + | |Horizontal dilation by a factor of <math>a</math> | ||
| + | |<math>f\left(x\times\tfrac{1}{a}\right)</math> | ||
| + | |Vertical dilation by a factor of <math>a</math> | ||
| + | |<math>a\times f(x)</math> | ||
| + | |- | ||
| + | |Vertical translation by <math>a</math> units '''down''' | ||
| + | |<math>f(x)-a</math> | ||
| + | |Vertical translation by <math>a</math> units '''up''' | ||
| + | |<math>f(x)+a</math> | ||
| + | |- | ||
| + | |Reflection about <math>x</math>-axis | ||
| + | |<math>-f(x)</math> | ||
| + | |Reflection about <math>y</math>-axis | ||
| + | |<math>f(-x)</math> | ||
| + | |} | ||
| − | For example, the | + | ==Inverse functions== |
| + | We call <math>g(x)</math> the inverse function of <math>f(x)</math> if, for all <math>x</math> : | ||
| + | :<math>g(f(x))=f(g(x))=x</math> | ||
| + | A function <math>f(x)</math> has an inverse function if and only if <math>f(x)</math> is one-to-one. For example, the inverse of <math>f(x)=x+2</math> is <math>g(x)=x-2</math> . The function <math>f(x)=\sqrt{1-x^2}</math> has no inverse because it is not injective. Similarly, the inverse functions of trigonometric functions have to undergo transformations and limitations to be considered as valid functions. | ||
| − | + | ===Notation=== | |
| + | The inverse function of <math>f</math> is denoted as <math>f^{-1}(x)</math> . Thus, <math>f^{-1}(x)</math> is defined as the function that follows this rule | ||
| + | :<math>f(f^{-1}(x))=f^{-1}(f(x))=x</math> | ||
| + | To determine <math>f^{-1}(x)</math> when given a function <math>f</math> , substitute <math>f^{-1}(x)</math> for <math>x</math> and substitute <math>x</math> for <math>f(x)</math> . Then solve for <math>f^{-1}(x)</math> , provided that it is also a function. | ||
| − | = | + | <b>Example:</b> Given <math>f(x)=2x-7</math> , find <math>f^{-1}(x)</math> . |
| − | |||
| − | |||
| − | + | Substitute <math>f^{-1}(x)</math> for <math>x</math> and substitute <math>x</math> for <math>f(x)</math> . Then solve for <math>f^{-1}(x)</math> : | |
| − | + | :<math>f(x)=2x-7</math> | |
| − | + | :<math>\Leftrightarrow x=2[f^{-1}(x)]-7</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [ | + | :<math>\Leftrightarrow x+7=2[f^{-1}(x)]</math> |
| − | + | :<math>\Leftrightarrow\frac{x+7}{2}=f^{-1}(x)</math> | |
| − | == | + | To check your work, confirm that <math>f^{-1}(f(x))=x</math> :<blockquote><math>f^{-1}(f(x))=</math><math>f^{-1}(2x-7)={}</math><math>\frac{(2x-7)+7}{2}=\frac{2x}{2}=x</math></blockquote>If <math>f</math> isn't one-to-one, then, as we said before, it doesn't have an inverse. Then this method will fail. |
| − | |||
| − | {{ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | ||
| − | = | + | '''Example:''' Given <math>f(x)=x^2</math> , find <math>f^{-1}(x)</math>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Substitute <math>f^{-1}(x)</math> for <math>x</math> and substitute <math>x</math> for <math>f(x)</math> . Then solve for <math>f^{-1}(x)</math> : | |
| − | { | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | { | ||
| − | = | + | :<math>f(x)=x^2</math> |
| − | |||
| − | = | + | :<math>x=(f^{-1}(x))^2</math> |
| − | { | ||
| − | + | :<math>f^{-1}(x)=\pm\sqrt{x}</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Since there are two possibilities for <math>f^{-1}(x)</math> , it's not a function. Thus <math>f(x)=x^2</math> doesn't have an inverse. Of course, we could also have found this out from the graph by applying the Horizontal Line Test. It's useful, though, to have lots of ways to solve a problem, since in a specific case some of them might be very difficult while others might be easy. For example, we might only know an algebraic expression for <math>f(x)</math> but not a graph. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Resources== |
| − | + | * [https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:functions/x2f8bb11595b61c86:evaluating-functions/v/what-is-a-function What is a Function?], Khan Academy | |
| − | * | + | * [https://www.khanacademy.org/math/algebra2/functions_and_graphs Function and their graphs], Khan Academy |
| − | * | + | * [https://www.cliffsnotes.com/study-guides/calculus/precalculus/functions/relations-vs-functions Relations vs. Functions], Cliff's Notes |
| − | * [ | + | * [https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/determine-whether-a-relation-represents-a-function/ Determining if a Relation is a Function], Lumen Learning |
| − | * [https:// | + | * [https://courses.lumenlearning.com/waymakercollegealgebra/chapter/identify-functions-using-graphs/ Identifying Functions Using Graphs], Lumen Learning |
| − | |||
| − | + | == Licensing == | |
| − | [ | + | Content obtained and/or adapted from: |
| − | + | * [https://en.wikibooks.org/wiki/Calculus/Functions Functions, Wikibooks: Calculus] under a CC BY-SA license | |
| − | |||
Latest revision as of 15:11, 15 January 2022
Contents
- 1 Introduction
- 2 Basic concepts of functions
- 3 Important functions
- 4 Properties of functions
- 5 Manipulating functions
- 6 Inverse functions
- 7 Resources
- 8 Licensing
Introduction
Formally, a function f from a set X to a set Y is defined by a set G of ordered pairs (x, y) such that x ∈ X, y ∈ Y, and every element of X is the first component of exactly one ordered pair in G. In other words, for every x in X, there is exactly one element y such that the ordered pair (x, y) belongs to the set of pairs defining the function f. The set G is called the graph of the function. Formally speaking, it may be identified with the function, but this hides the usual interpretation of a function as a process. Therefore, in common usage, the function is generally distinguished from its graph.}} Whenever one quantity uniquely determines the value of another quantity, we have a function. That is, the set uniquely determines the set . You can think of a function as a kind of machine. You feed the machine raw materials, and the machine changes the raw materials into a finished product.
Functions in everyday life
Think about dropping a ball from a bridge. At each moment in time, the ball is a height above the ground. The height of the ball is a function of time. It was the job of physicists to come up with a formula for this function. This type of function is called real-valued since the "finished product" is a number (or, more specifically, a real number).
Think about a wind storm. At different places, the wind can be blowing in different directions with different intensities. The direction and intensity of the wind can be thought of as a function of position. This is a function of two real variables (a location is described by two values - an and a ) which results in a vector (which is something that can be used to hold a direction and an intensity). These functions are studied in multivariable calculus (which is usually studied after a one year college level calculus course). This a vector-valued function of two real variables.
We will be looking at real-valued functions until studying multivariable calculus. Think of a real-valued function as an input-output machine; you give the function an input, and it gives you an output which is a number (more specifically, a real number). For example, the squaring function takes the input 4 and gives the output value 16. The same squaring function takes the input -1 and gives the output value 1.
Notation
Functions are used so much that there is a special notation for them. The notation is somewhat ambiguous, so familiarity with it is important in order to understand the intention of an equation or formula.
Though there are no strict rules for naming a function, it is standard practice to use the letters , , and to denote functions, and the variable to denote an independent variable. is used for both dependent and independent variables.
When discussing or working with a function , it's important to know not only the function, but also its independent variable . Thus, when referring to a function , you usually do not write , but instead . The function is now referred to as " of ". The name of the function is adjacent to the independent variable (in parentheses). This is useful for indicating the value of the function at a particular value of the independent variable. For instance, if
- ,
and if we want to use the value of for equal to , then we would substitute 2 for on both sides of the definition above and write
This notation is more informative than leaving off the independent variable and writing simply '' , but can be ambiguous since the parentheses next to can be misinterpreted as multiplication, . To make sure nobody is too confused, follow this procedure:
- Define the function by equating it to some expression.
- Give a sentence like the following: "At , the function is..."
- Evaluate the function.
Description
There are many ways which people describe functions. In the examples above, a verbal descriptions is given (the height of the ball above the earth as a function of time). Here is a list of ways to describe functions. The top three listed approaches to describing functions are the most popular.
- A function is given a name (such as ) and a formula for the function is also given. For example, describes a function. We refer to the input as the argument of the function (or the independent variable), and to the output as the value of the function at the given argument.
- A function is described using an equation and two variables. One variable is for the input of the function and one is for the output of the function. The variable for the input is called the independent variable. The variable for the output is called the dependent variable. For example, describes a function. The dependent variable appears by itself on the left hand side of equal sign.
- A verbal description of the function.
When a function is given a name (like in number 1 above), the name of the function is usually a single letter of the alphabet (such as or ). Some functions whose names are multiple letters (like the sine function
Plugging a value into a function
If we write , then we know that
- The function is a function of .
- To evaluate the function at a certain number, replace the with that number.
- Replacing with that number in the right side of the function will produce the function's output for that certain input.
- In English, the definition of is interpreted, "Given a number, will return two more than the triple of that number."
How would we know the value of the function at 3? We would have the following three thoughts:
and we would write
.
The value of at 3 is 11.
Note that means the value of the dependent variable when takes on the value of 3. So we see that the number 11 is the output of the function when we give the number 3 as the input. People often summarize the work above by writing "the value of at three is eleven", or simply " of three equals eleven".
Basic concepts of functions
The formal definition of a function states that a function is actually a mapping that associates the elements of one set called the domain of the function, , with the elements of another set called the range of the function, . For each value we select from the domain of the function, there exists exactly one corresponding element in the range of the function. The definition of the function tells us which element in the range corresponds to the element we picked from the domain. An example of how is given below.
Example
Let function for all . For what value of gives In mathematics, it is important to notice any repetition. If something seems to repeat, keep a note of that in the back of your mind somewhere.
Here, notice that and . Because is equal to two different things, it must be the case that the other side of the equal sign to is equal to the other. This property is known as the transitive property and could thus make the following equation below true:
Next, simplify — make your life easier rather than harder. In this instance, since has as a like-term, and the two terms are fractions added to the other, put it over a common denominator and simplify. Similar, since is a mixed fraction, .
Multiply both sides by the reciprocal of the coefficient of , from both sides by multiplying by it.
- or .
The value of that makes is .
Classically, the element picked from the domain is pictured as something that is fed into the function and the corresponding element in the range is pictured as the output. Since we "pick" the element in the domain whose corresponding element in the range we want to find, we have control over what element we pick and hence this element is also known as the "independent variable". The element mapped in the range is beyond our control and is "mapped to" by the function. This element is hence also known as the "dependent variable", for it depends on which independent variable we pick. Since the elementary idea of functions is better understood from the classical viewpoint, we shall use it hereafter. However, it is still important to remember the correct definition of functions at all times.
Basic types of transformation
To make it simple, for the function , all of the possible values constitute the domain, and all of the values ( on the x-y plane) constitute the range. To put it in more formal terms, a function is a mapping of some element , called the domain, to exactly one element , called the range, such that . The image below should help explain the modern definition of a function:
- A function is considered one-to-one if an element from domain of function , leads to exactly one element from range of the function. By definition, since only one element is mapped by function from some element , implies that there exists only one element from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to Figure 1.
- A function is considered many-to-one if some elements from domain of function maps to exactly one element from range of the function. Since some elements must map onto exactly one element , must be compliant with the definition of a function. Therefore, there exists a many-to-one function.
- A function is considered one-to-many if exactly one element from domain of function maps to some elements from range of the function. If some element maps onto many distinct elements , then is non-functional since there exists many distinct elements . Given many-to-one is non-compliant to the definition of a function, there exists no function that is one-to-many.
The modern definition describes a function sufficiently such that it helps us determine whether some new type of "function" is indeed one. Now that each case is defined above, you can now prove whether functions are one of these function cases. Here is an example problem:
One-to-One Example
Given: , where and are constant and .
Prove: function is one-to-one.}} Notice that the only changing element in the function is . To prove a function is one-to-one by applying the definition may be impossible because although two random elements of domain set may not be many-to-one, there may be some elements that may make the function many-to-one. To account for this possibility, we must prove that it is impossible to have some result like that.
Assume there exists two distinct elements that will result in . This would make the function many-to-one. In consequence,
Subtract from both sides of the equation.
Subtract from both sides of the equation.
Factor from both terms to the left of the equation.
Multiply to both sides of the equation.
Add to both sides of the equation.
Notice that . However, this is impossible because and are distinct. Ergo, . No two distinct inputs can give the same output. Therefore, the function must be one-to-one.
Basic concepts
There are a few more important ideas to learn from the modern definition of the function, and it comes from knowing the difference between domain, range, and codomain. We already discussed some of these, yet knowing about sets adds a new definition for each of the following ideas. Therefore, let us discuss these based on these new ideas. Let and be a set. If we were to combine these two sets, it would be defined as the cartesian cross product . The subset of this product is the function. The below definitions are a little confusing. The best way to interpret these is to draw an image. To the right of these definitions is the image that corresponds to it.
Definition of domain, range, and codomain of a function
The domain is defined to be a set with all elements mapping to at least one unique .
The set of elements in is the range of the function mapping in the cartesian cross product, whereby the set of all elements maps to some element .
The codomain is the set , where it is not necessarily the case that all elements was mapped by some .
Note that the codomain is not as important as the other two concepts.
Take for example:
Because of the square root, the content in the square root should be strictly not smaller than 0.
Thus the domain is
Correspondingly, the range will be
Other types of transformation
There is one more final aspect that needs to be defined. We already have a good idea of what makes a mapping a function (e.g. it cannot be one-to-many). However, three more definitions that you will often hear will be necessary to talk about: injective, surjective, bijective.
- A function is injective if it is one-to-one.
- A function is surjective if it is "onto." That is, the mapping has as the range of the function, where the codomain and the range of the function are the same.
- A function is bijective if it is both surjective and injective.
Again, the above definitions are often very confusing. Again, another image is provided to the right of the bullet points. Along with that, another example is also provided. Let us analyze the function .
Given: , where is constant and .
Prove: function is non-surjective and non-injective.
Notice that the only changing element in the function is . Let us check to see the conditions of this function.
Is it injective? Let , and solve for . First, divide by .
Then take the square root of . By definition, , so
Notice, however, what we learned from the above manipulation. As a result of solving for , we found that there are two solutions for . However, this resulted in two different values from . This means that for some individual that gives , there are two different inputs that result in the same value. Because when , this is by definition non-injective.
Is it surjective? As a natural consequence of what we learned about inputs, let us determine the range of the function. After all, the only way to determine if something is surjective is to see if the range applies to all real numbers. A good way to determine this is by finding a pattern involving our domains. Let us say we input a negative number for the domain: . This seemingly trivial exercise tells us that negative numbers give us non-negative numbers for our range. This is huge information! For , the function always results for our range. For the set , we have elements in that set that have no mappings from the set . As such, is the codomain of set . Therefore, this function is non-surjective!
Tests for equations
The vertical line test
The vertical line test is a systematic test to find out if an equation involving and can serve as a function (with the independent variable and the dependent variable). Simply graph the equation and draw a vertical line through each point of the -axis. If any vertical line ever touches the graph at more than one point, then the equation is not a function; if the line always touches at most one point of the graph, then the equation is a function.
The circle, on the right, is not a function because the vertical line intercepts two points on the graph when .
The horizontal line and the algebraic 1-1 test
Similarly, the horizontal line test, though does not test if an equation is a function, tests if a function is injective (one-to-one). If any horizontal line ever touches the graph at more than one point, then the function is not one-to-one; if the line always touches at most one point on the graph, then the function is one-to-one.
The algebraic 1-1 test is the non-geometric way to see if a function is one-to-one. The basic concept is that:
Assume there is a function . If:
, and , then
function is one-to-one.
Here is an example: prove that is injective.
Since the notation is the notation for a function, the equation is a function. So we only need to prove that it is injective. Let and be the inputs of the function and that . Thus,
So, the result is , proving that the function is injective.
Another example is proving that is not injective.
Using the same method, one can find that , which is not . So, the function is not injective.
Remarks
The following arise as a direct consequence of the definition of functions:
- By definition, for each "input" a function returns only one "output", corresponding to that input. While the same output may correspond to more than one input, one input cannot correspond to more than one output. This is expressed graphically as the vertical line test: a line drawn parallel to the axis of the dependent variable (normally vertical) will intersect the graph of a function only once. However, a line drawn parallel to the axis of the independent variable (normally horizontal) may intersect the graph of a function as many times as it likes. Equivalently, this has an algebraic (or formula-based) interpretation. We can always say if , then , but if we only know that then we can't be sure that .
- Each function has a set of values, the function's domain, which it can accept as input. Perhaps this set is all positive real numbers; perhaps it is the set {pork, mutton, beef}. This set must be implicitly/explicitly defined in the definition of the function. You cannot feed the function an element that isn't in the domain, as the function is not defined for that input element.
- Each function has a set of values, the function's range, which it can output. This may be the set of real numbers. It may be the set of positive integers or even the set {0,1}. This set, too, must be implicitly/explicitly defined in the definition of the function.
Functions are an important foundation of mathematics. This modern interpretation is a result of the hard work of the mathematicians of history. It was not until recently that the definition of the relation was introduced by René Descartes in Geometry (1637). Nearly a century later, the standard notation () was first introduced by Leonhard Euler in Introductio in Analysin Infinitorum and Institutiones Calculi Differentialis. The term function was also a new innovation during Euler's time as well, being introduced Gottfried Wilhelm Leibniz in a 1673 letter "to describe a quantity related to points of a curve, such as a coordinate or curve's slope." Finally, the modern definition of the function being the relation among sets was first introduced in 1908 by Godfrey Harold Hardy where there is a relation between two variables and such that "to some values of at any rate correspond values of ."
Important functions
Polynomials
Polynomial functions are the most common and most convenient functions in the world of calculus. Their frequent appearances and their applications on computer calculations have made them important. A polynomial in a single indeterminate x can always be written (or rewritten) in the form:
To be more concise, it can also be written in the summation form:
Constant
When , the polynomial can be rewritten into the following function:
, where is a constant.
The graph of this function is a horizontal line passing the point .
Linear
When , the polynomial can be rewritten into
, where are constants.
The graph of this function is a straight line passing the point and , and the slope of this function is .
Quadratic
When , the polynomial can be rewritten into
, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,b,c} are constants.
The graph of this function is a parabola, like the trajectory of a basketball thrown into the hoop.
If there are questions about the quadratic formula and other basic polynomial concepts, please review the respective chapters in Algebra.
Trigonometric
Trigonometric functions are also very important because it can connect algebra and geometry. Trigonometric functions are explained in detail here due to its importance and difficulty.
Exponential and Logarithmic
Exponential and logarithmic functions have a unique identity when calculating the derivatives, so this is a great time to review those functions. The exponential function is defined as:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=a^x} , where is a constant.
while the logarithmic function is defined as:
- , where is a constant.
A special number will be frequently seen in those functions: the Euler's constant, also known as the base of the natural logarithm. Notated as , it is defined as .
Signum
The Signum (sign) function is simply defined as
Properties of functions
Sometimes, a lot of function manipulations cannot be achieved without some help from basic properties of functions.
Domain and range
This concept is discussed above.
Growth
Although it seems obvious to spot a function increasing or decreasing, without the help of graphing software, we need a mathematical way to spot whether the function is increasing or decreasing, or else our human minds cannot immediately comprehend the huge amount of information.
Assume a function with inputs , and that , , and at all times.
If for all and , , then
is increasing in
If for all and , , then
is decreasing in
Example: In which intervals is increasing?
Firstly, the domain is important. Because the denominator cannot be 0, the domain for this function is
In , the growth of the function is:
Let and Thus,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because} both Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1,x_2\in[-\infty,-1]}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-x_2^2)(1-x_1^2)>0}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2>x_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1<x_2<0}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2^2-x_1^2<0}
So,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} is decreasing in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-\infty,-1)}
In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1,1)}
Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1,x_2\in[-1,1]} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2>x_1} Thus,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because} both Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1,x_2\in[-\infty,-1]}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-x_2^2)(1-x_1^2)>0}
However, the sign of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2^2-x_1^2} in cannot be determined. It can only be determined in .
In
and
In
As a result, is decreasing in and increasing in .
In
Let and Thus,
both Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1,x_2\in[-\infty,-1]}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-x_2^2)(1-x_1^2)>0}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because x_2>x_1\text{ and }0<x_1<x_2}
So, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_2)-f(x_1)=\frac{x_2^2-x_1^2}{(1-x_2^2)(1-x_1^2)}>0}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} is increasing in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,\infty)} .
Therefore, the intervals in which the function is increasing are Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,1)\And(1,\infty)} .
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \blacksquare}
After learning derivatives, there will be more ways to determine the growth of a function.
Parity
The properties odd and even are associated with symmetry. While even functions have a symmetry about the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis, odd functions are symmetric about the origin. In mathematical terms:
A function is even when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(-x)=f(x)} A function is odd when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(-x)=-f(x)}
Example: Prove that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=\frac{1}{1-x^2}} is an even function.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore f(x) } is an even function
Manipulating functions
Addition, Subtraction, Multiplication and Division of functions
For two real-valued functions, we can add the functions, multiply the functions, raised to a power, etc. For example:
- If we add the functions Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=3x+2} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=x^2} , we obtain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=x^2+3x+2} .
- If we subtract from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=x^2} , we obtain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=x^2-(3x+2)} . We can also write this as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=x^2-3x-2} .
- If we multiply the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=3x+2} and the function , we obtain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=(3x+2)x^2} . We can also write this as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=3x^3+2x^2} .
- If we divide the function by the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=x^2} , we obtain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\frac{3x+2}{x^2}} .
If a math problem wants you to add two functions and , there are two ways that the problem will likely be worded:
- If you are told that , that , that and asked about , then you are being asked to add two functions. Your answer would be .
- If you are told that , that and you are asked about , then you are being asked to add two functions. The addition of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} is called Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f+g} . Your answer would be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f+g)(x)=x^2+3x+2} .
Similar statements can be made for subtraction, multiplication and division.
Let and: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x)=x^2} . Let's add, subtract, multiply and divide.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (f+g)(x) &= f(x)+g(x)\\ &= (3x+2)+(x^2)\\ &= x^2+3x+2\, \end{align}} ,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (f-g)(x) &= f(x)-g(x)\\ &= (3x+2)-(x^2)\\ &= -x^2+3x+2\, \end{align}} ,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (f\times g)(x) &= f(x)\times g(x)\\ &= (3x+2)\times(x^2)\\ &= 3x^3+2x^2\, \end{align}} ,
- .
Composition of functions
We begin with a fun (and not too complicated) application of composition of functions before we talk about what composition of functions is.
Example: Dropping a ball If we drop a ball from a bridge which is 20 meters above the ground, then the height of our ball above the earth is a function of time. The physicists tell us that if we measure time in seconds and distance in meters, then the formula for height in terms of time is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h=-4.9t^2+20} . Suppose we are tracking the ball with a camera and always want the ball to be in the center of our picture. Suppose we have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=f(h)} The angle will depend upon the height of the ball above the ground and the height above the ground depends upon time. So the angle will depend upon time. This can be written as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=f(-4.9t^2+20)} . We replace Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} with what it is equal to. This is the essence of composition.
Composition of functions is another way to combine functions which is different from addition, subtraction, multiplication or division.
The value of a function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} depends upon the value of another variable Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} ; however, that variable could be equal to another function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} , so its value depends on the value of a third variable. If this is the case, then the first variable is a function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} of the third variable; this function (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} ) is called the composition of the other two functions (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} and ).
Example: Composing two functions Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=3x+2} and: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x)=x^2} . The composition of with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} is read as either "f composed with g" or "f of g of x."
Let
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(x)=f(g(x))}
Then
- .
Sometimes a math problem asks you compute Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f\circ g)(x)} when they want you to compute Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(g(x))} ,
Here, is the composition of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} and we write . Note that composition is not commutative:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(g(x))=3x^2+2} , and
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} g(f(x)) &= g(3x+2)\\ &= (3x+2)^2\\ &= 9x^2+12x+4\, . \end{align}}
- so .
Composition of functions is very common, mainly because functions themselves are common. For instance, squaring and sine are both functions:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mbox{square}(x)=x^2}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mbox{sine}(x)=\sin(x)}
Thus, the expression is a composition of functions:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin^2(x)}
(Note that this is not the same as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mbox{sine}(\mbox{square}(x))=\sin(x^2)} .) Since the function sine equals if ,
- .
Since the function square equals if ,
- .
Transformations
Transformations are a type of function manipulation that are very common. They consist of multiplying, dividing, adding or subtracting constants to either the input or the output. Multiplying by a constant is called dilation and adding a constant is called translation. Here are a few examples:
- Dilation
- Translation
- Dilation
- Translation
Translations and dilations can be either horizontal or vertical. Examples of both vertical and horizontal translations can be seen at right. The red graphs represent functions in their 'original' state, the solid blue graphs have been translated (shifted) horizontally, and the dashed graphs have been translated vertically.
Dilations are demonstrated in a similar fashion. The function
has had its input doubled. One way to think about this is that now any change in the input will be doubled. If I add one to , I add two to the input of , so it will now change twice as quickly. Thus, this is a horizontal dilation by because the distance to the -axis has been halved. A vertical dilation, such as
is slightly more straightforward. In this case, you double the output of the function. The output represents the distance from the -axis, so in effect, you have made the graph of the function 'taller'. Here are a few basic examples where is any positive constant:
| Original graph | Rotation about origin | ||
| Horizontal translation by units left | Horizontal translation by units right | ||
| Horizontal dilation by a factor of | Vertical dilation by a factor of | ||
| Vertical translation by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} units down | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)-a} | Vertical translation by units up | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)+a} |
| Reflection about Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} -axis | Reflection about Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(-x)} |
Inverse functions
We call the inverse function of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} if, for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} :
A function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} has an inverse function if and only if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} is one-to-one. For example, the inverse of is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x)=x-2} . The function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=\sqrt{1-x^2}} has no inverse because it is not injective. Similarly, the inverse functions of trigonometric functions have to undergo transformations and limitations to be considered as valid functions.
Notation
The inverse function of is denoted as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{-1}(x)} . Thus, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{-1}(x)} is defined as the function that follows this rule
To determine when given a function , substitute for and substitute for . Then solve for , provided that it is also a function.
Example: Given , find .
Substitute for and substitute for . Then solve for :
To check your work, confirm that :
If isn't one-to-one, then, as we said before, it doesn't have an inverse. Then this method will fail.
Example: Given , find .
Substitute for and substitute for . Then solve for :
Since there are two possibilities for , it's not a function. Thus doesn't have an inverse. Of course, we could also have found this out from the graph by applying the Horizontal Line Test. It's useful, though, to have lots of ways to solve a problem, since in a specific case some of them might be very difficult while others might be easy. For example, we might only know an algebraic expression for but not a graph.
Resources
- What is a Function?, Khan Academy
- Function and their graphs, Khan Academy
- Relations vs. Functions, Cliff's Notes
- Determining if a Relation is a Function, Lumen Learning
- Identifying Functions Using Graphs, Lumen Learning
Licensing
Content obtained and/or adapted from:
- Functions, Wikibooks: Calculus under a CC BY-SA license




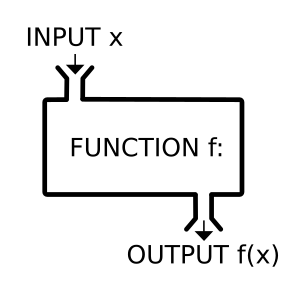































































![{\displaystyle x\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)

![{\displaystyle f(x)\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99f503c443788a9b9f65ff7a48589ce6fd1965d6)






















































![{\displaystyle x_{1}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f03ee615e7879f20efa45f3c3c6296c14b53995)
![{\displaystyle x_{2}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e93c068e15bd53700224ed82f922c758216ee03e)


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




![{\displaystyle x_{1},x_{2}\in [-\infty ,-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cf5c7151b951ae1ff019d7e81b7649743e9a8ac)













![{\displaystyle x_{1},x_{2}\in [1,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/740ee44dae32033ccc8b24018acf55e6c11fa60a)




































![{\displaystyle \Leftrightarrow x=2[f^{-1}(x)]-7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d823629e07ebfdf4e31604db723251807f12fd12)
![{\displaystyle \Leftrightarrow x+7=2[f^{-1}(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ef00069307c01d1d32178da59bf982da21648af)







