|
|
| Line 40: |
Line 40: |
| | *If the integrand contains <math>\sqrt{x^2-a^2}</math> let <math>x=a\sec(\theta)</math> and use the identity <math>\sec^2(\theta)-1=\tan^2(\theta)</math> . | | *If the integrand contains <math>\sqrt{x^2-a^2}</math> let <math>x=a\sec(\theta)</math> and use the identity <math>\sec^2(\theta)-1=\tan^2(\theta)</math> . |
| | </blockquote> | | </blockquote> |
| − | [[Image:Wikiversity-logo-Snorky.svg|right|thumb|80px|[[V:Trigonometric Substitutions|Trigonometric Substitutions]]]]
| |
| − | [[Image:Wikipedia-logo-en.png|right|thumb|80px|[[W:Trigonometric substitution|Trigonometric Substitutions]]]]
| |
| | | | |
| | ===Sine substitution=== | | ===Sine substitution=== |
| − | [[Image:Trig_Sub_Triangle_1.png|frame|right|273px|This substitution is easily derived from a triangle, using the [[w:Pythagorean_Theorem|Pythagorean Theorem]].]] | + | [[Image:Trig_Sub_Triangle_1.png|frame|right|273px|This substitution is easily derived from a triangle, using the Pythagorean Theorem.]] |
| | | | |
| | If the integrand contains a piece of the form <math>\sqrt{a^2-x^2}</math> we use the substitution | | If the integrand contains a piece of the form <math>\sqrt{a^2-x^2}</math> we use the substitution |
| Line 73: |
Line 71: |
| | | | |
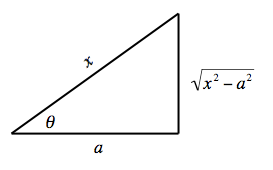
| | ===Tangent substitution=== | | ===Tangent substitution=== |
| − | [[Image:Trig_Sub_Triangle_2.png|frame|right|273px|This substitution is easily derived from a triangle, using the [[w:Pythagorean_Theorem|Pythagorean Theorem]].]] | + | [[Image:Trig_Sub_Triangle_2.png|frame|right|273px|This substitution is easily derived from a triangle, using the Pythagorean Theorem.]] |
| | | | |
| | When the integrand contains a piece of the form | | When the integrand contains a piece of the form |
The idea behind the trigonometric substitution is quite simple: to replace expressions involving square roots with expressions that involve standard trigonometric functions, but no square roots. Integrals involving trigonometric functions are often easier to solve than integrals involving square roots.
Let us demonstrate this idea in practice. Consider the expression  . Probably the most basic trigonometric identity is
. Probably the most basic trigonometric identity is  for an arbitrary angle
for an arbitrary angle  . If we replace
. If we replace  in this expression by
in this expression by  , with the help of this trigonometric identity we see
, with the help of this trigonometric identity we see

Note that we could write  since we replaced
since we replaced  with
with  .
.
We would like to mention that technically one should write the absolute value of  , in other words
, in other words  as our final answer since
as our final answer since  for all possible
for all possible  . But as long as we are careful about the domain of all possible
. But as long as we are careful about the domain of all possible  and how
and how  is used in the final computation, omitting the absolute value signs does not constitute a problem. However, we cannot directly interchange the simple expression
is used in the final computation, omitting the absolute value signs does not constitute a problem. However, we cannot directly interchange the simple expression  with the complicated
with the complicated  wherever it may appear, we must remember when integrating by substitution we need to take the derivative into account. That is we need to remember that
wherever it may appear, we must remember when integrating by substitution we need to take the derivative into account. That is we need to remember that  , and to get a integral that only involves
, and to get a integral that only involves  we need to also replace
we need to also replace  by something in terms of
by something in terms of  . Thus, if we see an
integral of the form
. Thus, if we see an
integral of the form

we can rewrite it as

Notice in the expression on the left that the first  comes from replacing the
comes from replacing the  and the
and the  comes from substituting for the
comes from substituting for the  .
.
Since  our original integral reduces to:
our original integral reduces to:
 .
.
These last two integrals are easily handled. For the first integral we get

For the second integral we do a substitution, namely  to get:
to get:

Finally we see that:

However, this is in terms of  and not in terms of
and not in terms of  , so we must substitute back in order to rewrite the answer in terms of
, so we must substitute back in order to rewrite the answer in terms of  .
.
That is we worked out that:

So we arrive at our final answer

As you can see, even for a fairly harmless looking integral this technique can involve quite a lot of calculation. Often it is helpful to see if a simpler method will suffice before turning to trigonometric substitution. On the other hand, frequently in the case of integrands involving square roots, this is the most tractable way to solve the problem. We begin with giving some rules of thumb to help you decide which trigonometric substitutions might be helpful.
If the integrand contains a single factor of one of the forms  we can try a trigonometric substitution.
we can try a trigonometric substitution.
- If the integrand contains
 let
let  and use the identity
and use the identity  .
.
- If the integrand contains
 let
let  and use the identity
and use the identity  .
.
- If the integrand contains
 let
let  and use the identity
and use the identity  .
.
Sine substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.
If the integrand contains a piece of the form  we use the substitution
we use the substitution

This will transform the integrand to a trigonometric function. If the new integrand can't be integrated on sight then the tan-half-angle substitution described below will generally transform it into a more tractable algebraic integrand.
E.g., if the integrand is  ,
,

If the integrand is  , we can rewrite it as
, we can rewrite it as

Then we can make the substitution
![{\displaystyle {\begin{aligned}\int \limits _{0}^{a}{\frac {1+x}{\sqrt {1-x^{2}}}}dx&=\int \limits _{0}^{\alpha }{\frac {1+\sin(\theta )}{\cos(\theta )}}\cos(\theta )d\theta &0<a<1\\&=\int \limits _{0}^{\alpha }{\bigl (}1+\sin(\theta ){\bigr )}d\theta &\alpha =\arcsin(a)\\&=\alpha +{\Big [}-\cos(\theta ){\Big ]}_{0}^{\alpha }\\&=\alpha +1-\cos(\alpha )\\&=1+\arcsin(a)-{\sqrt {1-a^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34bea926b8fc779d11222829c812acd2aa7561a)
Tangent substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.
When the integrand contains a piece of the form
 we use the substitution
we use the substitution

E.g., if the integrand is  then on making this substitution we find
then on making this substitution we find
![{\displaystyle {\begin{aligned}\int \limits _{0}^{z}(x^{2}+a^{2})^{-{\frac {3}{2}}}dx&=a^{-2}\int \limits _{0}^{\alpha }\cos(\theta )d\theta &z>0\\&=a^{-2}{\Big [}\sin(\theta ){\Big ]}_{0}^{\alpha }&\alpha =\arctan \left({\tfrac {z}{a}}\right)\\&=a^{-2}\sin(\alpha )\\&=a^{-2}{\frac {\frac {z}{a}}{\sqrt {1+{\frac {z^{2}}{a^{2}}}}}}\\&={\frac {z}{a^{2}{\sqrt {a^{2}+z^{2}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4664e0be89a175f0c7b393341bd8ad28bbeb24c)
If the integral is

then on making this substitution we find
![{\displaystyle {\begin{matrix}I&=&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &&&\alpha =\tan ^{-1}(z/a)\\&=&a^{2}\int _{0}^{\alpha }\sec \theta \,d\tan \theta &&&\\&=&a^{2}[\sec \theta \tan \theta ]_{0}^{\alpha }&-&a^{2}\int _{0}^{\alpha }\sec \theta \tan ^{2}\theta \,d\theta &\\&=&a^{2}\sec \alpha \tan \alpha &-&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\&=&a^{2}\sec \alpha \tan \alpha &-&I&+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313f2a452d4c096c9221cc6445317c894bb7eec0)
After integrating by parts, and using trigonometric identities, we've ended up with an expression involving the original integral. In cases like this we must now rearrange the equation so that the original integral is on one side only

|

|
|
|
![{\displaystyle ={\tfrac {a^{2}}{2}}{\Bigg (}\sec(\alpha )\tan(\alpha )+{\bigg [}\ln {\Big (}\sec(\theta )+\tan(\theta ){\Big )}{\bigg ]}_{0}^{\alpha }{\Bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ca73ab74b8a68988b561b211957b826c9bcc9f)
|
|
|

|
|
|

|
|
|

|
As we would expect from the integrand, this is approximately  for large
for large  .
.
In some cases it is possible to do trigonometric substitution in cases when there is no  appearing in the integral.
appearing in the integral.
Example

The denominator of this function is equal to  . This suggests that we try to substitute
. This suggests that we try to substitute  and use the identity
and use the identity  . With this substitution, we obtain that
. With this substitution, we obtain that  and thus
and thus




Using the initial substitution
 gives
gives

Secant substitution
If the integrand contains a factor of the form  we use the substitution
we use the substitution

Example 1
Find  .
.

|

|
|
|

|
|
|
![{\displaystyle ={\bigg [}\tan(\theta )-\theta {\bigg ]}_{0}^{\alpha }\qquad \qquad \qquad \tan(\alpha )={\sqrt {\sec ^{2}(\alpha )-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf30ca894dfeaff2a765bb3ddb822a60753c656)
|
|
|

|
|
|

|
Example 2
Find  .
.

|

|
|
|

|
We can now integrate by parts

|
![{\displaystyle =-{\bigg [}\tan(\theta )\cos(\theta ){\bigg ]}_{0}^{\alpha }+\int \limits _{0}^{\alpha }\sec(\theta )d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abddc762382184a13946dc8522620aa0ad23dff4)
|
|
|
![{\displaystyle =-\sin(\alpha )+{\bigg [}\ln {\bigl (}\sec(\theta )+\tan(\theta ){\bigr )}{\bigg ]}_{0}^{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b45d861d862f65be50d6cf40c62770494cfa763)
|
|
|

|
|
|

|
Resources
Licensing
Content obtained and/or adapted from:










































![{\displaystyle {\begin{aligned}\int \limits _{0}^{a}{\frac {1+x}{\sqrt {1-x^{2}}}}dx&=\int \limits _{0}^{\alpha }{\frac {1+\sin(\theta )}{\cos(\theta )}}\cos(\theta )d\theta &0<a<1\\&=\int \limits _{0}^{\alpha }{\bigl (}1+\sin(\theta ){\bigr )}d\theta &\alpha =\arcsin(a)\\&=\alpha +{\Big [}-\cos(\theta ){\Big ]}_{0}^{\alpha }\\&=\alpha +1-\cos(\alpha )\\&=1+\arcsin(a)-{\sqrt {1-a^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34bea926b8fc779d11222829c812acd2aa7561a)



![{\displaystyle {\begin{aligned}\int \limits _{0}^{z}(x^{2}+a^{2})^{-{\frac {3}{2}}}dx&=a^{-2}\int \limits _{0}^{\alpha }\cos(\theta )d\theta &z>0\\&=a^{-2}{\Big [}\sin(\theta ){\Big ]}_{0}^{\alpha }&\alpha =\arctan \left({\tfrac {z}{a}}\right)\\&=a^{-2}\sin(\alpha )\\&=a^{-2}{\frac {\frac {z}{a}}{\sqrt {1+{\frac {z^{2}}{a^{2}}}}}}\\&={\frac {z}{a^{2}{\sqrt {a^{2}+z^{2}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4664e0be89a175f0c7b393341bd8ad28bbeb24c)

![{\displaystyle {\begin{matrix}I&=&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &&&\alpha =\tan ^{-1}(z/a)\\&=&a^{2}\int _{0}^{\alpha }\sec \theta \,d\tan \theta &&&\\&=&a^{2}[\sec \theta \tan \theta ]_{0}^{\alpha }&-&a^{2}\int _{0}^{\alpha }\sec \theta \tan ^{2}\theta \,d\theta &\\&=&a^{2}\sec \alpha \tan \alpha &-&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\&=&a^{2}\sec \alpha \tan \alpha &-&I&+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313f2a452d4c096c9221cc6445317c894bb7eec0)


![{\displaystyle ={\tfrac {a^{2}}{2}}{\Bigg (}\sec(\alpha )\tan(\alpha )+{\bigg [}\ln {\Big (}\sec(\theta )+\tan(\theta ){\Big )}{\bigg ]}_{0}^{\alpha }{\Bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ca73ab74b8a68988b561b211957b826c9bcc9f)






















![{\displaystyle ={\bigg [}\tan(\theta )-\theta {\bigg ]}_{0}^{\alpha }\qquad \qquad \qquad \tan(\alpha )={\sqrt {\sec ^{2}(\alpha )-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf30ca894dfeaff2a765bb3ddb822a60753c656)





![{\displaystyle =-{\bigg [}\tan(\theta )\cos(\theta ){\bigg ]}_{0}^{\alpha }+\int \limits _{0}^{\alpha }\sec(\theta )d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abddc762382184a13946dc8522620aa0ad23dff4)
![{\displaystyle =-\sin(\alpha )+{\bigg [}\ln {\bigl (}\sec(\theta )+\tan(\theta ){\bigr )}{\bigg ]}_{0}^{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b45d861d862f65be50d6cf40c62770494cfa763)

