Difference between revisions of "Trigonometric Substitution"
(Added video links) |
|||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | The idea behind the trigonometric substitution is quite simple: to replace expressions involving square roots with expressions that involve standard trigonometric functions, but ''no square roots''. Integrals involving trigonometric functions are often easier to solve than integrals involving square roots. | |
| − | + | Let us demonstrate this idea in practice. Consider the expression <math>\sqrt{1-x^2}</math> . Probably the most basic trigonometric identity is <math>\sin^2(\theta)+\cos^2(\theta)=1</math> for an arbitrary angle <math>\theta</math> . If we replace <math>x</math> in this expression by <math>\sin(\theta)</math> , with the help of this trigonometric identity we see | |
| + | :<math>\sqrt{1-x^2}=\sqrt{1-\sin^2(\theta)}=\sqrt{\cos^2(\theta)}=\cos(\theta)</math> | ||
| + | Note that we could write <math>\theta=\arcsin(x)</math> since we replaced <math>x^2</math> with <math>\sin^2(\theta)</math> . | ||
| − | + | We would like to mention that technically one should write the absolute value of <math>\cos(\theta)</math> , in other words <math>\bigl|\cos(\theta)\bigr|</math> as our final answer since <math>\sqrt{a^2}=|a|</math> for all possible <math>a</math> . But as long as we are careful about the domain of all possible <math>x</math> and how <math>\cos(\theta)</math> is used in the final computation, omitting the absolute value signs does not constitute a problem. However, we cannot directly interchange the simple expression <math>\cos(\theta)</math> with the complicated <math>\sqrt{1-x^2}</math> wherever it may appear, we must remember when integrating by substitution we need to take the derivative into account. That is we need to remember that <math>dx=\cos(\theta)d\theta</math> , and to get a integral that only involves <math>\theta</math> we need to also replace <math>dx</math> by something in terms of <math>d\theta</math> . Thus, if we see an | |
| + | integral of the form | ||
| + | :<math>\int\sqrt{1-x^2}dx</math> | ||
| + | we can rewrite it as | ||
| + | :<math>\int\cos(\theta)\cos(\theta)d\theta=\int\cos^2(\theta)d\theta</math> | ||
| + | Notice in the expression on the left that the first <math>\cos(\theta)</math> comes from replacing the <math>\sqrt{1-x^2}</math> and the <math>\cos(\theta)d\theta</math> comes from substituting for the <math>dx</math> . | ||
| − | + | Since <math>\cos^2(\theta)=\frac{1+\cos(2\theta)}{2}</math> our original integral reduces to: | |
| + | :<math>\tfrac12\int d\theta+\tfrac12\int\cos(2\theta)d\theta</math> . | ||
| − | + | These last two integrals are easily handled. For the first integral we get | |
| + | :<math>\tfrac12\int d\theta=\tfrac12\theta</math> | ||
| − | + | For the second integral we do a substitution, namely <math>u=2\theta,du=2d\theta</math> to get: | |
| + | :<math>\tfrac12\int\cos(2\theta)d\theta=\tfrac12\int\cos(u)\tfrac12du=\tfrac14\sin(u)=\frac{\sin(2\theta)}{4}</math> | ||
| − | + | Finally we see that: | |
| + | :<math>\int\cos^2(\theta)d\theta=\frac{\theta}{2}+\frac{\sin(2\theta)}{4}=\frac{\theta+\sin(\theta)\cos(\theta)}{2}</math> | ||
| + | However, this is in terms of <math>\theta</math> and not in terms of <math>x</math> , so we must substitute back in order to rewrite the answer in terms of <math>x</math> . | ||
| − | + | That is we worked out that: | |
| + | :<math>\sin(\theta)=x\qquad\cos(\theta)=\sqrt{1-x^2}\qquad\theta=\arcsin(x)</math> | ||
| − | + | So we arrive at our final answer | |
| + | :<math>\int\sqrt{1-x^2}dx=\frac{\arcsin(x)+x\sqrt{1-x^2}}{2}</math> | ||
| − | [https://youtu.be/wuRNmNDLanc Trigonometric Substitution More Examples] by patrickJMT | + | As you can see, even for a fairly harmless looking integral this technique can involve quite a lot of calculation. Often it is helpful to see if a simpler method will suffice before turning to trigonometric substitution. On the other hand, frequently in the case of integrands involving square roots, this is the most tractable way to solve the problem. We begin with giving some rules of thumb to help you decide which trigonometric substitutions might be helpful. |
| + | |||
| + | If the integrand contains a single factor of one of the forms <math>\sqrt{a^2-x^2}\mbox{ or }\sqrt{a^2+x^2}\mbox{ or }\sqrt{x^2-a^2}</math> we can try a trigonometric substitution. | ||
| + | |||
| + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | ||
| + | *If the integrand contains <math>\sqrt{a^2-x^2}</math> let <math>x=a\sin(\theta)</math> and use the identity <math>1-\sin^2(\theta)=\cos^2(\theta)</math> . | ||
| + | *If the integrand contains <math>\sqrt{a^2+x^2}</math> let <math>x=a\tan(\theta)</math> and use the identity <math>1+\tan^2(\theta)=\sec^2(\theta)</math> . | ||
| + | *If the integrand contains <math>\sqrt{x^2-a^2}</math> let <math>x=a\sec(\theta)</math> and use the identity <math>\sec^2(\theta)-1=\tan^2(\theta)</math> . | ||
| + | </blockquote> | ||
| + | |||
| + | ===Sine substitution=== | ||
| + | [[Image:Trig_Sub_Triangle_1.png|frame|right|273px|This substitution is easily derived from a triangle, using the Pythagorean Theorem.]] | ||
| + | |||
| + | If the integrand contains a piece of the form <math>\sqrt{a^2-x^2}</math> we use the substitution | ||
| + | :<math>x=a\sin(\theta)\quad dx=a\cos(\theta)d\theta</math> | ||
| + | This will transform the integrand to a trigonometric function. If the new integrand can't be integrated on sight then the tan-half-angle substitution described below will generally transform it into a more tractable algebraic integrand. | ||
| + | |||
| + | E.g., if the integrand is <math>\sqrt{1-x^2}</math> , | ||
| + | |||
| + | :<math>\begin{align} | ||
| + | \int\limits_0^1\sqrt{1-x^2}dx&=\int\limits_0^\frac{\pi}{2}\sqrt{1-\sin^2(\theta)}\cos(\theta)d\theta\\ | ||
| + | &=\int\limits_0^\frac{\pi}{2}\cos^2(\theta)d\theta\\ | ||
| + | &=\tfrac12\int\limits_0^\frac{\pi}{2}\bigl(1+\cos(2\theta)\bigr)d\theta\\ | ||
| + | &=\frac{\pi}{4} | ||
| + | \end{align}</math> | ||
| + | |||
| + | If the integrand is <math>\sqrt{\frac{1+x}{1-x}}</math> , we can rewrite it as | ||
| + | :<math>\sqrt{\frac{1+x}{1-x}}=\sqrt{\frac{1+x}{1+x}\cdot\frac{1+x}{1-x}}=\frac{1+x}{\sqrt{1-x^2}}</math> | ||
| + | Then we can make the substitution | ||
| + | |||
| + | :<math>\begin{align} | ||
| + | \int\limits_0^a\frac{1+x}{\sqrt{1-x^2}}dx&=\int\limits_0^\alpha\frac{1+\sin(\theta)}{\cos(\theta)}\cos(\theta)d\theta | ||
| + | &0<a<1\\ | ||
| + | &=\int\limits_0^\alpha\bigl(1+\sin(\theta)\bigr)d\theta&\alpha=\arcsin(a)\\ | ||
| + | &=\alpha+\Big[-\cos(\theta)\Big]_0^\alpha\\ | ||
| + | &=\alpha+1-\cos(\alpha)\\ | ||
| + | &=1+\arcsin(a)-\sqrt{1-a^2} | ||
| + | \end{align}</math> | ||
| + | |||
| + | ===Tangent substitution=== | ||
| + | [[Image:Trig_Sub_Triangle_2.png|frame|right|273px|This substitution is easily derived from a triangle, using the Pythagorean Theorem.]] | ||
| + | |||
| + | When the integrand contains a piece of the form | ||
| + | <math>\sqrt{a^2+x^2}</math> | ||
| + | we use the substitution | ||
| + | :<math>x=a\tan(\theta)\qquad\sqrt{x^2+a^2}=a\sec(\theta)\qquad dx=a\sec^2(\theta)d\theta</math> | ||
| + | |||
| + | E.g., if the integrand is <math>(x^2+a^2)^{-\frac32}</math> then on making this substitution we find | ||
| + | |||
| + | :<math>\begin{align} | ||
| + | \int\limits_0^z(x^2+a^2)^{-\frac32}dx&=a^{-2}\int\limits_0^\alpha \cos(\theta)d\theta&z>0\\ | ||
| + | &=a^{-2}\Big[\sin(\theta)\Big]_0^\alpha&\alpha=\arctan\left(\tfrac{z}{a}\right)\\ | ||
| + | &=a^{-2}\sin(\alpha)\\ | ||
| + | &=a^{-2}\frac{\frac{z}{a}}{\sqrt{1+\frac{z^2}{a^2}}}\\ | ||
| + | &=\frac{z}{a^2\sqrt{a^2+z^2}} | ||
| + | \end{align}</math> | ||
| + | |||
| + | If the integral is | ||
| + | |||
| + | :<math>I=\int\limits_0^z\sqrt{x^2+a^2}\qquad z>0</math> | ||
| + | |||
| + | then on making this substitution we find | ||
| + | |||
| + | :<math>\begin{matrix} | ||
| + | I & = & a^2 \int_0^\alpha \sec^3 \theta \, d\theta | ||
| + | & & & \alpha = \tan^{-1} (z/a) \\ | ||
| + | & = & a^2 \int_0^\alpha \sec \theta \, d\tan \theta & & & \\ | ||
| + | & = & a^2 [ \sec \theta \tan \theta ]_0^\alpha & - & | ||
| + | a^2 \int_0^\alpha \sec \theta \tan^2 \theta \, d\theta & \\ | ||
| + | & = & a^2 \sec \alpha \tan \alpha & - | ||
| + | & a^2 \int_0^\alpha \sec^3 \theta \, d\theta & + | ||
| + | a^2 \int_0^\alpha \sec \theta \, d\theta \\ | ||
| + | & = & a^2 \sec \alpha \tan \alpha & - | ||
| + | & I & + a^2 \int_0^\alpha \sec \theta \, d\theta \\ | ||
| + | \end{matrix}</math> | ||
| + | |||
| + | After integrating by parts, and using trigonometric identities, we've ended up with an expression involving the original integral. In cases like this we must now rearrange the equation so that the original integral is on one side only | ||
| + | |||
| + | :{| | ||
| + | |<math>I</math> | ||
| + | |<math>=\tfrac{a^2}{2}\Bigg(\sec(\alpha)\tan(\alpha)+\int\limits_0^\alpha \sec(\theta)d\theta\Bigg)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\tfrac{a^2}{2}\Bigg(\sec(\alpha)\tan(\alpha)+\bigg[\ln\Big(\sec(\theta)+\tan(\theta)\Big)\bigg]_0^\alpha\Bigg)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\tfrac{a^2}{2}\bigg(\sec(\alpha)\tan(\alpha)+a^2\ln\Big(\sec(\alpha)+\tan(\alpha)\Big)\bigg)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\tfrac{a^2}{2}\bigg(\tfrac{z}{a^2}\sqrt{a^2+z^2}+\ln\left(\tfrac{z+\sqrt{a^2+z^2}}{a}\right)\bigg)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\tfrac{1}{2}\bigg(z\sqrt{z^2+a^2}+a^2\ln\left(\tfrac{z+\sqrt{a^2+z^2}}{a}\right)\bigg)</math> | ||
| + | |} | ||
| + | |||
| + | As we would expect from the integrand, this is approximately <math>\frac{z^2}{2}</math> for large <math>z</math> . | ||
| + | |||
| + | In some cases it is possible to do trigonometric substitution in cases when there is no <math>\sqrt{\ \ }</math> appearing in the integral. | ||
| + | |||
| + | '''Example''' | ||
| + | :<math>\int\frac{dx}{x^2+1}</math> | ||
| + | |||
| + | The denominator of this function is equal to <math>\bigl(\sqrt{1+x^2}\bigr)^2</math> . This suggests that we try to substitute <math>x=\tan(u)</math> and use the identity <math>1+\tan^2(u)=\sec^2(u)</math> . With this substitution, we obtain that <math>dx=\sec^2(u)du</math> and thus | ||
| + | :<math>\int\frac{dx}{x^2+1}=\int\frac{\sec^2(u)}{\tan^2(u)+1}du</math> | ||
| + | |||
| + | :<math>=\int\frac{\sec^2(u)}{\sec^2(u)}du</math> | ||
| + | :<math>=\int du</math> | ||
| + | :<math>=u+c</math> | ||
| + | Using the initial substitution | ||
| + | <math>u=\arctan(x)</math> | ||
| + | gives | ||
| + | :<math>\int\frac{dx}{x^2+1}=\arctan(x)+C</math> | ||
| + | |||
| + | ===Secant substitution=== | ||
| + | [[Image:Trig_Sub_Triangle_3.png|frame|right|273px|This substitution is easily derived from a triangle, using the [[w:Pythagorean_Theorem|Pythagorean Theorem]].]] | ||
| + | |||
| + | If the integrand contains a factor of the form <math>\displaystyle\sqrt{x^2-a^2}</math> we use the substitution | ||
| + | :<math>x=a\sec(\theta)\quad dx=a\sec(\theta)\tan(\theta)d\theta\quad\sqrt{x^2-a^2}=a\tan(\theta)</math> | ||
| + | |||
| + | ==== Example 1 ==== | ||
| + | Find <math>\int\limits_0^z \frac{\sqrt{x^2-1}}{x}dx</math> . | ||
| + | |||
| + | :{| | ||
| + | |<math>\int\limits_0^z \frac{\sqrt{x^2-1}}{x}dx</math> | ||
| + | |<math>=\int\limits_0^\alpha \frac{\tan(\theta)}{\sec(\theta)}\sec(\theta)\tan(\theta)d\theta\qquad z>1</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\int\limits_0^\alpha \tan^2(\theta)d\theta\qquad\qquad\qquad\qquad\alpha=\arcsec(z)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\bigg[\tan(\theta)-\theta\bigg]_0^\alpha\qquad\qquad\qquad\tan(\alpha)=\sqrt{\sec^2(\alpha)-1}</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\tan(\alpha)-\alpha\qquad\qquad\qquad\qquad\tan(\alpha)=\sqrt{z^2-1}</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\sqrt{z^2-1}-\arcsec(z)</math> | ||
| + | |} | ||
| + | |||
| + | ==== Example 2 ==== | ||
| + | Find <math>\int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx</math> . | ||
| + | |||
| + | :{| | ||
| + | |<math>\int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx</math> | ||
| + | |<math>=\int\limits_1^\alpha \frac{\tan(\theta)}{\sec^2(\theta)}\sec(\theta)\tan(\theta)d\theta\qquad z>1</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\int\limits_0^\alpha \frac{\sin^2(\theta)}{\cos(\theta)}d\theta\qquad\qquad\qquad\alpha=\arcsec(z)</math> | ||
| + | |} | ||
| + | |||
| + | We can now integrate by parts | ||
| + | :{| | ||
| + | |<math>\int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx</math> | ||
| + | |<math>=-\bigg[\tan(\theta)\cos(\theta)\bigg]_0^\alpha+\int\limits_0^\alpha \sec(\theta)d\theta</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=-\sin(\alpha)+\bigg[\ln\bigl(\sec(\theta)+ \tan(\theta)\bigr)\bigg]_0^\alpha</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\ln\bigl(\sec(\alpha)+\tan(\alpha)\bigr)-\sin(\alpha)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=\ln\bigl(z+\sqrt{z^2-1}\bigr)-\frac{\sqrt{z^2-1}}{z}</math> | ||
| + | |} | ||
| + | |||
| + | ==Resources== | ||
| + | *[https://youtu.be/BVn8x7wCa3A Ex 1: Integration Using Trigonometric Substitution] by James Sousa | ||
| + | |||
| + | *[https://youtu.be/a-f63vZVuBQ Ex 2: Integration Using Trigonometric Substitution] by James Sousa | ||
| + | |||
| + | *[https://youtu.be/jZa4FM6l6pM Ex 3: Integration Using Trigonometric Substitution] by James Sousa | ||
| + | |||
| + | *[https://youtu.be/ObxsrPx44nw Ex 4: Integration Using Trigonometric Substitution] by James Sousa | ||
| + | |||
| + | *[https://youtu.be/OnT7Ub68FWg Ex 5: Integration Using Trigonometric Substitution] by James Sousa | ||
| + | |||
| + | *[https://youtu.be/3lC5AuCFK4c Trigonometric Substitution - Example 1] by patrickJMT | ||
| + | |||
| + | *[https://youtu.be/GVL4lHX6DgM Trigonometric Substitution - Example 2] by patrickJMT | ||
| + | |||
| + | *[https://youtu.be/yW6Odu0YHL0 Trigonometric Substitution - Example 3 Part 1] by patrickJMT | ||
| + | |||
| + | *[https://youtu.be/4QNntd_KZbc Trigonometric Substitution - Example 4 Rational Powers] by patrickJMT | ||
| + | |||
| + | *[https://youtu.be/wuRNmNDLanc Trigonometric Substitution More Examples] by patrickJMT | ||
| + | |||
| + | ==Licensing== | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Integration_techniques/Trigonometric_Substitution Trigonometric Substitution, Wikibooks: Calculus/Integration techniques] under a CC BY-SA license | ||
Latest revision as of 17:36, 15 January 2022
The idea behind the trigonometric substitution is quite simple: to replace expressions involving square roots with expressions that involve standard trigonometric functions, but no square roots. Integrals involving trigonometric functions are often easier to solve than integrals involving square roots.
Let us demonstrate this idea in practice. Consider the expression . Probably the most basic trigonometric identity is for an arbitrary angle . If we replace in this expression by , with the help of this trigonometric identity we see
Note that we could write since we replaced with .
We would like to mention that technically one should write the absolute value of , in other words as our final answer since for all possible . But as long as we are careful about the domain of all possible and how is used in the final computation, omitting the absolute value signs does not constitute a problem. However, we cannot directly interchange the simple expression with the complicated wherever it may appear, we must remember when integrating by substitution we need to take the derivative into account. That is we need to remember that , and to get a integral that only involves we need to also replace by something in terms of . Thus, if we see an integral of the form
we can rewrite it as
Notice in the expression on the left that the first comes from replacing the and the comes from substituting for the .
Since our original integral reduces to:
- .
These last two integrals are easily handled. For the first integral we get
For the second integral we do a substitution, namely to get:
Finally we see that:
However, this is in terms of and not in terms of , so we must substitute back in order to rewrite the answer in terms of .
That is we worked out that:
So we arrive at our final answer
As you can see, even for a fairly harmless looking integral this technique can involve quite a lot of calculation. Often it is helpful to see if a simpler method will suffice before turning to trigonometric substitution. On the other hand, frequently in the case of integrands involving square roots, this is the most tractable way to solve the problem. We begin with giving some rules of thumb to help you decide which trigonometric substitutions might be helpful.
If the integrand contains a single factor of one of the forms we can try a trigonometric substitution.
- If the integrand contains let and use the identity .
- If the integrand contains let and use the identity .
- If the integrand contains let and use the identity .
Contents
Sine substitution
If the integrand contains a piece of the form we use the substitution
This will transform the integrand to a trigonometric function. If the new integrand can't be integrated on sight then the tan-half-angle substitution described below will generally transform it into a more tractable algebraic integrand.
E.g., if the integrand is ,
If the integrand is , we can rewrite it as
Then we can make the substitution
Tangent substitution
When the integrand contains a piece of the form we use the substitution
E.g., if the integrand is then on making this substitution we find
If the integral is
then on making this substitution we find
After integrating by parts, and using trigonometric identities, we've ended up with an expression involving the original integral. In cases like this we must now rearrange the equation so that the original integral is on one side only
As we would expect from the integrand, this is approximately for large .
In some cases it is possible to do trigonometric substitution in cases when there is no appearing in the integral.
Example
The denominator of this function is equal to . This suggests that we try to substitute and use the identity . With this substitution, we obtain that and thus
Using the initial substitution gives
Secant substitution
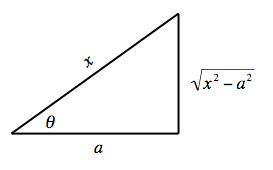
If the integrand contains a factor of the form we use the substitution
Example 1
Find .
Example 2
Find .
We can now integrate by parts
Resources
- Ex 1: Integration Using Trigonometric Substitution by James Sousa
- Ex 2: Integration Using Trigonometric Substitution by James Sousa
- Ex 3: Integration Using Trigonometric Substitution by James Sousa
- Ex 4: Integration Using Trigonometric Substitution by James Sousa
- Ex 5: Integration Using Trigonometric Substitution by James Sousa
- Trigonometric Substitution - Example 1 by patrickJMT
- Trigonometric Substitution - Example 2 by patrickJMT
- Trigonometric Substitution - Example 3 Part 1 by patrickJMT
- Trigonometric Substitution - Example 4 Rational Powers by patrickJMT
- Trigonometric Substitution More Examples by patrickJMT
Licensing
Content obtained and/or adapted from:
- Trigonometric Substitution, Wikibooks: Calculus/Integration techniques under a CC BY-SA license










































![{\displaystyle {\begin{aligned}\int \limits _{0}^{a}{\frac {1+x}{\sqrt {1-x^{2}}}}dx&=\int \limits _{0}^{\alpha }{\frac {1+\sin(\theta )}{\cos(\theta )}}\cos(\theta )d\theta &0<a<1\\&=\int \limits _{0}^{\alpha }{\bigl (}1+\sin(\theta ){\bigr )}d\theta &\alpha =\arcsin(a)\\&=\alpha +{\Big [}-\cos(\theta ){\Big ]}_{0}^{\alpha }\\&=\alpha +1-\cos(\alpha )\\&=1+\arcsin(a)-{\sqrt {1-a^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34bea926b8fc779d11222829c812acd2aa7561a)



![{\displaystyle {\begin{aligned}\int \limits _{0}^{z}(x^{2}+a^{2})^{-{\frac {3}{2}}}dx&=a^{-2}\int \limits _{0}^{\alpha }\cos(\theta )d\theta &z>0\\&=a^{-2}{\Big [}\sin(\theta ){\Big ]}_{0}^{\alpha }&\alpha =\arctan \left({\tfrac {z}{a}}\right)\\&=a^{-2}\sin(\alpha )\\&=a^{-2}{\frac {\frac {z}{a}}{\sqrt {1+{\frac {z^{2}}{a^{2}}}}}}\\&={\frac {z}{a^{2}{\sqrt {a^{2}+z^{2}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4664e0be89a175f0c7b393341bd8ad28bbeb24c)

![{\displaystyle {\begin{matrix}I&=&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &&&\alpha =\tan ^{-1}(z/a)\\&=&a^{2}\int _{0}^{\alpha }\sec \theta \,d\tan \theta &&&\\&=&a^{2}[\sec \theta \tan \theta ]_{0}^{\alpha }&-&a^{2}\int _{0}^{\alpha }\sec \theta \tan ^{2}\theta \,d\theta &\\&=&a^{2}\sec \alpha \tan \alpha &-&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\&=&a^{2}\sec \alpha \tan \alpha &-&I&+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313f2a452d4c096c9221cc6445317c894bb7eec0)


![{\displaystyle ={\tfrac {a^{2}}{2}}{\Bigg (}\sec(\alpha )\tan(\alpha )+{\bigg [}\ln {\Big (}\sec(\theta )+\tan(\theta ){\Big )}{\bigg ]}_{0}^{\alpha }{\Bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ca73ab74b8a68988b561b211957b826c9bcc9f)






















![{\displaystyle ={\bigg [}\tan(\theta )-\theta {\bigg ]}_{0}^{\alpha }\qquad \qquad \qquad \tan(\alpha )={\sqrt {\sec ^{2}(\alpha )-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf30ca894dfeaff2a765bb3ddb822a60753c656)





![{\displaystyle =-{\bigg [}\tan(\theta )\cos(\theta ){\bigg ]}_{0}^{\alpha }+\int \limits _{0}^{\alpha }\sec(\theta )d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abddc762382184a13946dc8522620aa0ad23dff4)
![{\displaystyle =-\sin(\alpha )+{\bigg [}\ln {\bigl (}\sec(\theta )+\tan(\theta ){\bigr )}{\bigg ]}_{0}^{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b45d861d862f65be50d6cf40c62770494cfa763)

