Difference between revisions of "Functions:Definition"

From Department of Mathematics at UTSA
Jump to navigation Jump to search
 
(2 intermediate revisions by one other user not shown)
Line 1: Line 1:
−
[[File:Arrow diagram of a function (non-injective and non-surjective).svg|thumb|Example of an arrow diagram of a function <math> f:A\to B </math>]]
+
== Functions ==
 +
A function is a relationship between two sets of numbers. We may think of this as a ''mapping''; a function ''maps'' a number in one set to a number in another set.  Notice that a function maps values to '''one and only one''' value. Two values in one set could map to one value, but one value '''must never''' map to two values: that would be a relation, ''not'' a function.
  
−
A function (or "mapping") is a relationship between two sets <math> A </math> and <math> B </math> that maps each input <math> a\in A </math> to exactly one output <math> b\in B </math>. A function <math> f </math> that maps elements of the set <math> A </math> to elements in the set <math> B </math> is denoted as <math> f: A\to B </math>, where <math> A </math> is the domain of <math> f </math> and <math> B </math> is the codomain. We can also think of a function <math> f: A\to B </math> as a set of ordered pairs <math> (a, b) </math>, <math> a\in A </math> and <math> b\in B </math>, such that each element <math> a </math> is paired with exactly one element <math> b </math>. If a function <math> f: A\to B </math> maps an input <math> a </math> to an output <math> b </math>, we can write that <math> f(a) = b </math>. For finite, reasonably small sets, we can depict a function graphically (see image).
+
{| align="right"
 +
|-
 +
| [[Image:Allowed_mapping_for_a_function.png]]
 +
|}
  
−
Note: a function cannot map one input to more than one output, but it can map more than one input to the same output. For example, let <math> A = \{a_1, a_2\} </math> and <math> B = \{b_1, b_2\} </math>, <math> a_1\neq a_2 </math> and <math> b_1\neq b_2 </math>. If <math> f: A\to B </math> is a relation such that <math> f(a_1) = b_1 </math> and <math> f(a_1) = b_2 </math>, then <math> f </math> is NOT a function. However, a relation <math> g: A\to B </math> such that <math> g(a_1) = b_1 </math> and <math> g(a_2) = b_1 </math> IS a valid function.
+
For example, if we write (define) a function as:
 +
: <math>f(x)=x^2</math>
 +
then we say:
 +
:'f of x equals x squared'
 +
and we have
 +
: <math>f(-1)=1</math>
 +
: <math>f(1)=1</math>
 +
: <math>f(7)=49</math>
 +
: <math>f(1/2)=1/4</math>
 +
:<math>f(4)=16</math>
 +
and so on.
  
 +
This function f maps numbers to their squares.
  
−
Examples:
+
=== Range and codomain ===
−
* Let <math> A = \{1, 2, 3, 4, 5\} </math> and <math> B = \{-1, 3, 4\} </math>, and let <math> f: A\to B </math> such that <math> f(1) = -1  </math>, <math> f(2) = 3  </math>, <math> f(3) = 4  </math>, <math> f(4) = 3  </math>, and <math> f(5) = -1  </math>. Since each element of the domain maps to exactly one element (that is, there is no <math> f(a) = b_1 </math> and <math> f(a) = b_2 </math> such that <math> b_1 \neq b_2 </math>), <math> f </math> is a function.
+
If D is a set, we can say
 +
: <math>f(D) = \{f(x) |\ x \in D\}</math>
  
−
* For sets <math> A </math> and <math> B </math> in the previous example, let <math> g: A\to B </math> be a relation such that <math> g(1) = 1 </math>, <math> g(1) = 3 </math>, <math> g(2) = 4 </math>, <math> g(4) = 4 </math>, and <math> g(5) = 4 </math>. Since <math> g </math> maps the input <math> 1 </math> to two distinct outputs, this relation is NOT a valid function.
+
which forms a née of f is usually a subset of a larger set. This set is known as the ''codomain'' of a function. For example, with the function f(''x'')=cos ''x'', the range of f is [-1,1], '''but''' the codomain is the set of real numbers.
  
−
* Let <math> f: \N\to\N </math> such that <math> f(n) = n + 1 </math>. This is a function, since each <math> n\in\N </math> maps to exactly one element <math> n+1\in\N </math>.
+
=== Notations ===
 +
When we have a function f, with domain D and range R, we write:
 +
:<math>f : D \longrightarrow R</math>
  
−
* Let <math> g: \N\to\Z </math> such that <math> |g(n)| = n </math>. This is not a valid function, since for <math> n\in\N </math>, <math> g(n) </math> can equal both <math> n </math> and <math> -n </math>, and <math> n\neq -n </math> for <math> n\neq 0 </math>.
+
If we say that, for instance, ''x'' is mapped to ''x''<sup>2</sup>, we also can add
 +
:<math>f : D \longrightarrow R;\ x \longmapsto x^2</math>
 +
 
 +
Notice that we can have a function that maps a point (''x'',''y'') to a real number, or some other function of two variables -- we have a set of ordered pairs as the domain. Recall from set theory that this is defined by the ''Cartesian product'' - if we wish to represent a set of all real-valued ordered pairs we can take the Cartesian product of the real numbers with itself to obtain
 +
:<math>\mathbb{R}\times\mathbb{R}=\mathbb{R}^2=\{(x,y)|\ x\ \mbox{and}\ y \in\mathbb{R}\}</math>.
 +
When we have a set of ''n''-tuples as part of the domain, we say that the function is ''n''-ary (for numbers ''n''=1,2 we say unary, and binary respectively).
 +
=== Other function notation ===
 +
Functions can be written as above, but we can also write them in two other ways. One way is to use an arrow diagram to represent the mappings between each element. We write the elements from the domain on one side, and the elements from the range on the other, and we draw arrows to show that an element from the domain is mapped to the range.
 +
 
 +
For example, for the function f(''x'')=''x''<sup>3</sup>, the arrow diagram for the domain {1,2,3} would be:
 +
[[Image:Arrow diagram example.jpg]]
 +
 
 +
Another way is to use set notation. If f(''x'')=''y'', we can write the function in terms of its mappings. This idea is best to show in an example.
 +
 
 +
Let us take the domain D={1,2,3}, and f(''x'')=''x''<sup>2</sup>. Then, the range of f will be R={f(1),f(2),f(3)}={1,4,9}. Taking the Cartesian product of D and R we obtain F={(1,1),(2,4),(3,9)}.
 +
 
 +
So using set notation, a function can be expressed as the Cartesian product of its domain and range.
 +
f(''x'')
 +
This function is called ''f'', and it takes a ''variable'' ''x''. We substitute some value for ''x'' to get the second value, which is what the function maps x to.
 +
 
 +
===Types of functions===
 +
Functions can either be '''''one to one (injective), onto (surjective), or bijective'''''.
 +
 +
''<u>'''INJECTIVE Functions'''</u>'' are functions in which every element in the domain maps into a unique elements in the codomain.
 +
 
 +
''<u>'''SURJECTIVE Functions'''</u>'' are functions in which every element in the codomain is mapped by an element in the domain.
 +
 
 +
<u>''''''BIJECTIVE''' Functions</u>''' are functions that are both injective and surjective.
 +
 
 +
---onto functions '''</u>''' a function f form A to B is onto ,
  
 
==Resources==
 
==Resources==
 
* [https://link-springer-com.libweb.lib.utsa.edu/content/pdf/10.1007%2F978-1-4419-7127-2.pdf Course Textbook], pages 129-140
 
* [https://link-springer-com.libweb.lib.utsa.edu/content/pdf/10.1007%2F978-1-4419-7127-2.pdf Course Textbook], pages 129-140
 
* [https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/A_Spiral_Workbook_for_Discrete_Mathematics_(Kwong)/06%3A_Functions/6.02%3A_De%EF%AC%81nition_of_Functions Definition of Functions], Mathematics LibreTexts
 
* [https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/A_Spiral_Workbook_for_Discrete_Mathematics_(Kwong)/06%3A_Functions/6.02%3A_De%EF%AC%81nition_of_Functions Definition of Functions], Mathematics LibreTexts
 +
 +
== Licensing ==
 +
Content obtained and/or adapted from:
 +
* [https://en.wikibooks.org/wiki/Discrete_Mathematics/Functions_and_relations Functions and relations, Wikibooks: Discrete Mathematics] under a CC BY-SA license

Latest revision as of 15:50, 11 November 2021

Functions

A function is a relationship between two sets of numbers. We may think of this as a mapping; a function maps a number in one set to a number in another set. Notice that a function maps values to one and only one value. Two values in one set could map to one value, but one value must never map to two values: that would be a relation, not a function.

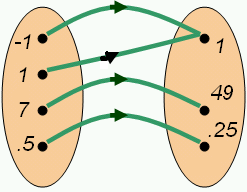
Allowed mapping for a function.png

For example, if we write (define) a function as:

then we say:

'f of x equals x squared'

and we have

and so on.

This function f maps numbers to their squares.

Range and codomain

If D is a set, we can say

which forms a née of f is usually a subset of a larger set. This set is known as the codomain of a function. For example, with the function f(x)=cos x, the range of f is [-1,1], but the codomain is the set of real numbers.

Notations

When we have a function f, with domain D and range R, we write:

If we say that, for instance, x is mapped to x2, we also can add

Notice that we can have a function that maps a point (x,y) to a real number, or some other function of two variables -- we have a set of ordered pairs as the domain. Recall from set theory that this is defined by the Cartesian product - if we wish to represent a set of all real-valued ordered pairs we can take the Cartesian product of the real numbers with itself to obtain

.

When we have a set of n-tuples as part of the domain, we say that the function is n-ary (for numbers n=1,2 we say unary, and binary respectively).

Other function notation

Functions can be written as above, but we can also write them in two other ways. One way is to use an arrow diagram to represent the mappings between each element. We write the elements from the domain on one side, and the elements from the range on the other, and we draw arrows to show that an element from the domain is mapped to the range.

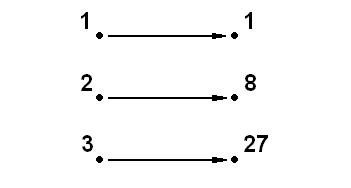
For example, for the function f(x)=x3, the arrow diagram for the domain {1,2,3} would be: Arrow diagram example.jpg

Another way is to use set notation. If f(x)=y, we can write the function in terms of its mappings. This idea is best to show in an example.

Let us take the domain D={1,2,3}, and f(x)=x2. Then, the range of f will be R={f(1),f(2),f(3)}={1,4,9}. Taking the Cartesian product of D and R we obtain F={(1,1),(2,4),(3,9)}.

So using set notation, a function can be expressed as the Cartesian product of its domain and range. 

f(x)

This function is called f, and it takes a variable x. We substitute some value for x to get the second value, which is what the function maps x to.

Types of functions

Functions can either be one to one (injective), onto (surjective), or bijective.

INJECTIVE Functions are functions in which every element in the domain maps into a unique elements in the codomain.

SURJECTIVE Functions are functions in which every element in the codomain is mapped by an element in the domain.

'BIJECTIVE' Functions are functions that are both injective and surjective.

---onto functions a function f form A to B is onto ,

Resources

Licensing

Content obtained and/or adapted from:

Retrieved from "https://mathresearch.utsa.edu/wiki/index.php?title=Functions:Definition&oldid=3781"