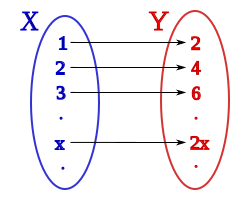Difference between revisions of "Sets:Countable"
| (5 intermediate revisions by one other user not shown) | |||
| Line 22: | Line 22: | ||
==Introduction== | ==Introduction== | ||
| − | A '' | + | A ''set'' is a collection of ''elements'', and may be described in many ways. One way is simply to list all of its elements; for example, the set consisting of the integers 3, 4, and 5 may be denoted {3, 4, 5}, called roster form. This is only effective for small sets, however; for larger sets, this would be time-consuming and error-prone. Instead of listing every single element, sometimes an ellipsis ("...") is used to represent many elements between the starting element and the end element in a set, if the writer believes that the reader can easily guess what ... represents; for example, {1, 2, 3, ..., 100} presumably denotes the set of integers from 1 to 100. Even in this case, however, it is still ''possible'' to list all the elements, because number of elements in the set is finite. |
| − | Some sets are ''infinite''; these sets have more than ''n'' elements where ''n'' is any integer that can be specified. (No matter how large the specified integer ''n'' is, such as ''n'' = 9 × 10<sup>32</sup>, infinite sets have more than ''n'' elements.) For example, the set of natural numbers, denotable by {0, 1, 2, 3, 4, 5, ...}, | + | Some sets are ''infinite''; these sets have more than ''n'' elements where ''n'' is any integer that can be specified. (No matter how large the specified integer ''n'' is, such as ''n'' = 9 × 10<sup>32</sup>, infinite sets have more than ''n'' elements.) For example, the set of natural numbers, denotable by {0, 1, 2, 3, 4, 5, ...}, has infinitely many elements, and we cannot use any natural number to give its size. Nonetheless, it turns out that infinite sets do have a well-defined notion of size (or more properly, ''cardinality'', the technical term for the number of elements in a set), and not all infinite sets have the same cardinality. |
[[File:Aplicación 2 inyectiva sobreyectiva02.svg|thumb|x100px|Bijective mapping from integer to even numbers]] | [[File:Aplicación 2 inyectiva sobreyectiva02.svg|thumb|x100px|Bijective mapping from integer to even numbers]] | ||
| − | To understand what this means, we first examine what it ''does not'' mean. For example, there are infinitely many odd integers, infinitely many even integers, and (hence) infinitely many integers overall. However, it turns out that the number of even integers, which is the same as the number of odd integers, is also the same as the number of integers overall. This is because we can arrange things such that, for every integer, there is a distinct even integer:<math display="block">\ldots \, -\! 2\! \rightarrow \! - \! 4, \, -\! 1\! \rightarrow \! - \! 2, \, 0\! \rightarrow \! 0, \, 1\! \rightarrow \! 2, \, 2\! \rightarrow \! 4 \, \ldots</math>or, more generally, <math>n \rightarrow 2n</math> (see picture). What we have done here is arrange the integers and the even integers into a ''one-to-one correspondence'' (or '' | + | To understand what this means, we first examine what it ''does not'' mean. For example, there are infinitely many odd integers, infinitely many even integers, and (hence) infinitely many integers overall. However, it turns out that the number of even integers, which is the same as the number of odd integers, is also the same as the number of integers overall. This is because we can arrange things such that, for every integer, there is a distinct even integer:<math display="block">\ldots \, -\! 2\! \rightarrow \! - \! 4, \, -\! 1\! \rightarrow \! - \! 2, \, 0\! \rightarrow \! 0, \, 1\! \rightarrow \! 2, \, 2\! \rightarrow \! 4 \, \ldots</math>or, more generally, <math>n \rightarrow 2n</math> (see picture). What we have done here is arrange the integers and the even integers into a ''one-to-one correspondence'' (or ''bijection''), which is a function that maps between two sets such that each element of each set corresponds to a single element in the other set. |
| − | However, not all infinite sets have the same cardinality. For example, | + | However, not all infinite sets have the same cardinality. For example, Georg Cantor (who introduced this concept) demonstrated that the real numbers cannot be put into one-to-one correspondence with the natural numbers (non-negative integers), and therefore that the set of real numbers has a greater cardinality than the set of natural numbers. |
==Formal overview== | ==Formal overview== | ||
| − | By definition, a set ''S'' is ''countable'' if there exists an | + | By definition, a set ''S'' is ''countable'' if there exists an injective function ''f'' : ''S'' → '''N''' from ''S'' to the natural numbers '''N''' = {0, 1, 2, 3, ...}. It simply means that every element in ''S'' has the correspondence to a different element in '''N'''''.'' |
It might seem natural to divide the sets into different classes: put all the sets containing one element together; all the sets containing two elements together; ...; finally, put together all infinite sets and consider them as having the same size. | It might seem natural to divide the sets into different classes: put all the sets containing one element together; all the sets containing two elements together; ...; finally, put together all infinite sets and consider them as having the same size. | ||
This view is not tenable, however, under the natural definition of size. | This view is not tenable, however, under the natural definition of size. | ||
| − | To elaborate this, we need the concept of a | + | To elaborate this, we need the concept of a bijection. Although a "bijection" may seem a more advanced concept than a number, the usual development of mathematics in terms of set theory defines functions before numbers, as they are based on much simpler sets. This is where the concept of a bijection comes in: define the correspondence |
:''a'' ↔ 1, ''b'' ↔ 2, ''c'' ↔ 3 | :''a'' ↔ 1, ''b'' ↔ 2, ''c'' ↔ 3 | ||
| Line 45: | Line 45: | ||
We now generalize this situation; we ''define'' that two sets are of the same size, if and only if there is a bijection between them. For all finite sets, this gives us the usual definition of "the same size". | We now generalize this situation; we ''define'' that two sets are of the same size, if and only if there is a bijection between them. For all finite sets, this gives us the usual definition of "the same size". | ||
| − | As for the case of infinite sets, consider the sets ''A'' = {1, 2, 3, ... }, the set of positive | + | As for the case of infinite sets, consider the sets ''A'' = {1, 2, 3, ... }, the set of positive integers, and ''B'' = {2, 4, 6, ... }, the set of even positive integers. We claim that, under our definition, these sets have the same size, and that therefore ''B'' is countably infinite. Recall that to prove this, we need to exhibit a bijection between them. This can be achieved using the assignment ''n'' ↔ 2''n'', so that |
:1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, .... | :1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, .... | ||
| − | As in the earlier example, every element of A has been paired off with precisely one element of B, and vice versa. Hence they have the same size. This is an example of a set of the same size as one of its | + | As in the earlier example, every element of A has been paired off with precisely one element of B, and vice versa. Hence they have the same size. This is an example of a set of the same size as one of its proper subsets, which is impossible for finite sets. |
| − | Likewise, the set of all | + | Likewise, the set of all ordered pairs of natural numbers (the Cartesian product of two sets of natural numbers, '''N''' × '''N''') is countably infinite, as can be seen by following a path like the one in the picture: [[File:Pairing natural.svg|thumb|300px|The Cantor pairing function assigns one natural number to each pair of natural numbers]] The resulting mapping proceeds as follows: |
:0 ↔ (0, 0), 1 ↔ (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), .... | :0 ↔ (0, 0), 1 ↔ (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), .... | ||
This mapping covers all such ordered pairs. | This mapping covers all such ordered pairs. | ||
| − | This form of triangular mapping | + | This form of triangular mapping recursively generalizes to ''n''-tuples of natural numbers, i.e., (''a<sub>1</sub>'', ''a<sub>2</sub>'', ''a<sub>3</sub>'', ..., ''a<sub>n</sub>'') where ''a<sub>i</sub>'' and ''n'' are natural numbers, by repeatedly mapping the first two elements of a ''n''-tuple to a natural number. For example, (0, 2, 3) can be written as ((0, 2), 3). Then (0, 2) maps to 5 so ((0, 2), 3) maps to (5, 3), then (5, 3) maps to 39. Since a different 2-tuple, that is a pair such as (''a'', ''b''), maps to a different natural number, a difference between two n-tuples by a single element is enough to ensure the n-tuples being mapped to different natural numbers. So, an injection from the set of ''n''-tuples to the set of natural numbers '''N''' is proved. For the set of n-tuples made by the Cartesian product of finitely many different sets, each element in each tuple has the correspondence to a natural number, so every tuple can be written in natural numbers then the same logic is applied to prove the theorem. |
| − | '''Theorem:''' The | + | '''Theorem:''' The Cartesian product of finitely many countable sets is countable. |
| − | |||
| − | |||
| − | |||
| − | The set of all | + | The set of all integers '''Z''' and the set of all rational numbers '''Q''' may intuitively seem much bigger than '''N'''. But looks can be deceiving. If a pair is treated as the numerator and denominator of a vulgar fraction (a fraction in the form of ''a''/''b'' where ''a'' and ''b'' ≠ 0 are integers), then for every positive fraction, we can come up with a distinct natural number corresponding to it. This representation also includes the natural numbers, since every natural number is also a fraction ''N''/1. So we can conclude that there are exactly as many positive rational numbers as there are positive integers. This is also true for all rational numbers, as can be seen below. |
| − | '''Theorem:''' '''Z''' (the set of all integers) and '''Q''' (the set of all rational numbers) are countable. | + | '''Theorem:''' '''Z''' (the set of all integers) and '''Q''' (the set of all rational numbers) are countable. |
| − | In a similar manner, the set of | + | In a similar manner, the set of algebraic numbers is countable. |
| − | Sometimes more than one mapping is useful: a set A to be shown as countable is one-to-one mapped (injection) to another set B, then A is proved as countable if B is one-to-one mapped to the set of natural numbers. For example, the set of positive | + | Sometimes more than one mapping is useful: a set A to be shown as countable is one-to-one mapped (injection) to another set B, then A is proved as countable if B is one-to-one mapped to the set of natural numbers. For example, the set of positive rational numbers can easily be one-to-one mapped to the set of natural number pairs (2-tuples) because ''p''/''q ''maps to (''p'', ''q''). Since the set of natural number pairs is one-to-one mapped (actually one-to-one correspondence or bijection) to the set of natural numbers as shown above, the positive rational number set is proved as countable. |
| − | '''Theorem:''' Any finite | + | '''Theorem:''' Any finite union of countable sets is countable. |
| − | |||
| − | |||
| − | |||
With the foresight of knowing that there are uncountable sets, we can wonder whether or not this last result can be pushed any further. The answer is "yes" and "no", we can extend it, but we need to assume a new axiom to do so. | With the foresight of knowing that there are uncountable sets, we can wonder whether or not this last result can be pushed any further. The answer is "yes" and "no", we can extend it, but we need to assume a new axiom to do so. | ||
| − | '''Theorem:''' (Assuming the | + | '''Theorem:''' (Assuming the axiom of countable choice) The union of countably many countable sets is countable. |
For example, given countable sets '''a''', '''b''', '''c''', ... | For example, given countable sets '''a''', '''b''', '''c''', ... | ||
| Line 96: | Line 90: | ||
*... | *... | ||
| − | This only works if the sets '''a''', '''b''', '''c''', ... are | + | This only works if the sets '''a''', '''b''', '''c''', ... are disjoint. If not, then the union is even smaller and is therefore also countable by a previous theorem. |
| − | We need the | + | We need the axiom of countable choice to index ''all'' the sets '''a''', '''b''', '''c''', ... simultaneously. |
| − | '''Theorem:''' The set of all finite-length | + | '''Theorem:''' The set of all finite-length sequences of natural numbers is countable. |
This set is the union of the length-1 sequences, the length-2 sequences, the length-3 sequences, each of which is a countable set (finite Cartesian product). So we are talking about a countable union of countable sets, which is countable by the previous theorem. | This set is the union of the length-1 sequences, the length-2 sequences, the length-3 sequences, each of which is a countable set (finite Cartesian product). So we are talking about a countable union of countable sets, which is countable by the previous theorem. | ||
| − | '''Theorem:''' The set of all finite | + | '''Theorem:''' The set of all finite subsets of the natural numbers is countable. |
The elements of any finite subset can be ordered into a finite sequence. There are only countably many finite sequences, so also there are only countably many finite subsets. | The elements of any finite subset can be ordered into a finite sequence. There are only countably many finite sequences, so also there are only countably many finite subsets. | ||
| Line 112: | Line 106: | ||
# If the function ''g'' : ''S'' → ''T'' is surjective and ''S'' is countable then ''T'' is countable. | # If the function ''g'' : ''S'' → ''T'' is surjective and ''S'' is countable then ''T'' is countable. | ||
| − | These follow from the definitions of countable set as injective / surjective functions | + | These follow from the definitions of countable set as injective / surjective functions. |
| − | + | '''Cantor's theorem''' asserts that if ''A'' is a set and ''P''(''A'') is its power set, i.e. the set of all subsets of ''A'', then there is no surjective function from ''A'' to ''P''(''A''). A proof is given in the article Cantor's theorem. As an immediate consequence of this and the Basic Theorem above we have: | |
| − | |||
| − | ''' | + | '''Proposition:''' The set ''P''('''N''') is not countable; i.e. it is uncountable. |
| − | + | The set of real numbers is uncountable, and so is the set of all infinite sequences of natural numbers. | |
| − | |||
| − | |||
| − | |||
| − | The set of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Total orders== | ==Total orders== | ||
| − | Countable sets can be | + | Countable sets can be totally ordered in various ways, for example: |
| − | * | + | *Well-orders (see also ordinal number): |
**The usual order of natural numbers (0, 1, 2, 3, 4, 5, ...) | **The usual order of natural numbers (0, 1, 2, 3, 4, 5, ...) | ||
**The integers in the order (0, 1, 2, 3, ...; −1, −2, −3, ...) | **The integers in the order (0, 1, 2, 3, ...; −1, −2, −3, ...) | ||
| Line 144: | Line 125: | ||
In both examples of well orders here, any subset has a ''least element''; and in both examples of non-well orders, ''some'' subsets do not have a ''least element''. | In both examples of well orders here, any subset has a ''least element''; and in both examples of non-well orders, ''some'' subsets do not have a ''least element''. | ||
This is the key definition that determines whether a total order is also a well order. | This is the key definition that determines whether a total order is also a well order. | ||
| + | |||
| + | == Licensing == | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikipedia.org/wiki/Countable_set Countable set, Wikipedia] under a CC BY-SA license | ||
Latest revision as of 14:03, 6 November 2021
In mathematics, a countable set is a set with the same cardinality (number of elements) as some subset of the set of natural numbers. A countable set is either a finite set or a countably infinite set. Whether finite or infinite, the elements of a countable set can always be counted one at a time and—although the counting may never finish—every element of the set is associated with a unique natural number.
Georg Cantor introduced the concept of countable sets, contrasting sets that are countable with those that are uncountable. Today, countable sets form the foundation of a branch of mathematics called discrete mathematics.
Contents
A note on terminology
Although the terms "countable" and "countably infinite" as defined here are quite common, the terminology is not universal. An alternative style uses countable to mean what is here called countably infinite, and at most countable to mean what is here called countable. To avoid ambiguity, one may limit oneself to the terms "at most countable" and "countably infinite", although with respect to concision this is the worst of both worlds. The reader is advised to check the definition in use when encountering the term "countable" in the literature.
The terms enumerable may also be used, e.g. referring to countable and countably infinite respectively, but as definitions vary the reader is once again advised to check the definition in use.
Definition
The most concise definition is in terms of cardinality. A set S is countable if its cardinality |S| is less than or equal to (aleph-null), the cardinality of the set of natural numbers N. A set S is countably infinite if |S| = . A set is uncountable if it is not countable, i.e. its cardinality is greater than .
Equivalently, a set S is countable iff:
- there exists an injective function from S to N.
- S is empty or there exists a surjective function from N to S, or .
- there exists a bijective mapping between S and a subset of N.
- S is either finite or countably infinite.
Similarly, a set S is countably infinite iff:
- there is an injective and surjective (and therefore bijective) mapping between S and N. In other words, a set is countably infinite if it has one-to-one correspondence with the natural number set, N.
- The elements of S can be arranged in an infinite sequence , where is distinct from for and every element of S is listed.
Introduction
A set is a collection of elements, and may be described in many ways. One way is simply to list all of its elements; for example, the set consisting of the integers 3, 4, and 5 may be denoted {3, 4, 5}, called roster form. This is only effective for small sets, however; for larger sets, this would be time-consuming and error-prone. Instead of listing every single element, sometimes an ellipsis ("...") is used to represent many elements between the starting element and the end element in a set, if the writer believes that the reader can easily guess what ... represents; for example, {1, 2, 3, ..., 100} presumably denotes the set of integers from 1 to 100. Even in this case, however, it is still possible to list all the elements, because number of elements in the set is finite.
Some sets are infinite; these sets have more than n elements where n is any integer that can be specified. (No matter how large the specified integer n is, such as n = 9 × 1032, infinite sets have more than n elements.) For example, the set of natural numbers, denotable by {0, 1, 2, 3, 4, 5, ...}, has infinitely many elements, and we cannot use any natural number to give its size. Nonetheless, it turns out that infinite sets do have a well-defined notion of size (or more properly, cardinality, the technical term for the number of elements in a set), and not all infinite sets have the same cardinality.
To understand what this means, we first examine what it does not mean. For example, there are infinitely many odd integers, infinitely many even integers, and (hence) infinitely many integers overall. However, it turns out that the number of even integers, which is the same as the number of odd integers, is also the same as the number of integers overall. This is because we can arrange things such that, for every integer, there is a distinct even integer:
However, not all infinite sets have the same cardinality. For example, Georg Cantor (who introduced this concept) demonstrated that the real numbers cannot be put into one-to-one correspondence with the natural numbers (non-negative integers), and therefore that the set of real numbers has a greater cardinality than the set of natural numbers.
Formal overview
By definition, a set S is countable if there exists an injective function f : S → N from S to the natural numbers N = {0, 1, 2, 3, ...}. It simply means that every element in S has the correspondence to a different element in N.
It might seem natural to divide the sets into different classes: put all the sets containing one element together; all the sets containing two elements together; ...; finally, put together all infinite sets and consider them as having the same size. This view is not tenable, however, under the natural definition of size.
To elaborate this, we need the concept of a bijection. Although a "bijection" may seem a more advanced concept than a number, the usual development of mathematics in terms of set theory defines functions before numbers, as they are based on much simpler sets. This is where the concept of a bijection comes in: define the correspondence
- a ↔ 1, b ↔ 2, c ↔ 3
Since every element of {a, b, c} is paired with precisely one element of {1, 2, 3}, and vice versa, this defines a bijection.
We now generalize this situation; we define that two sets are of the same size, if and only if there is a bijection between them. For all finite sets, this gives us the usual definition of "the same size".
As for the case of infinite sets, consider the sets A = {1, 2, 3, ... }, the set of positive integers, and B = {2, 4, 6, ... }, the set of even positive integers. We claim that, under our definition, these sets have the same size, and that therefore B is countably infinite. Recall that to prove this, we need to exhibit a bijection between them. This can be achieved using the assignment n ↔ 2n, so that
- 1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....
As in the earlier example, every element of A has been paired off with precisely one element of B, and vice versa. Hence they have the same size. This is an example of a set of the same size as one of its proper subsets, which is impossible for finite sets.
Likewise, the set of all ordered pairs of natural numbers (the Cartesian product of two sets of natural numbers, N × N) is countably infinite, as can be seen by following a path like the one in the picture:
The resulting mapping proceeds as follows:
- 0 ↔ (0, 0), 1 ↔ (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), ....
This mapping covers all such ordered pairs.
This form of triangular mapping recursively generalizes to n-tuples of natural numbers, i.e., (a1, a2, a3, ..., an) where ai and n are natural numbers, by repeatedly mapping the first two elements of a n-tuple to a natural number. For example, (0, 2, 3) can be written as ((0, 2), 3). Then (0, 2) maps to 5 so ((0, 2), 3) maps to (5, 3), then (5, 3) maps to 39. Since a different 2-tuple, that is a pair such as (a, b), maps to a different natural number, a difference between two n-tuples by a single element is enough to ensure the n-tuples being mapped to different natural numbers. So, an injection from the set of n-tuples to the set of natural numbers N is proved. For the set of n-tuples made by the Cartesian product of finitely many different sets, each element in each tuple has the correspondence to a natural number, so every tuple can be written in natural numbers then the same logic is applied to prove the theorem.
Theorem: The Cartesian product of finitely many countable sets is countable.
The set of all integers Z and the set of all rational numbers Q may intuitively seem much bigger than N. But looks can be deceiving. If a pair is treated as the numerator and denominator of a vulgar fraction (a fraction in the form of a/b where a and b ≠ 0 are integers), then for every positive fraction, we can come up with a distinct natural number corresponding to it. This representation also includes the natural numbers, since every natural number is also a fraction N/1. So we can conclude that there are exactly as many positive rational numbers as there are positive integers. This is also true for all rational numbers, as can be seen below.
Theorem: Z (the set of all integers) and Q (the set of all rational numbers) are countable.
In a similar manner, the set of algebraic numbers is countable.
Sometimes more than one mapping is useful: a set A to be shown as countable is one-to-one mapped (injection) to another set B, then A is proved as countable if B is one-to-one mapped to the set of natural numbers. For example, the set of positive rational numbers can easily be one-to-one mapped to the set of natural number pairs (2-tuples) because p/q maps to (p, q). Since the set of natural number pairs is one-to-one mapped (actually one-to-one correspondence or bijection) to the set of natural numbers as shown above, the positive rational number set is proved as countable.
Theorem: Any finite union of countable sets is countable.
With the foresight of knowing that there are uncountable sets, we can wonder whether or not this last result can be pushed any further. The answer is "yes" and "no", we can extend it, but we need to assume a new axiom to do so.
Theorem: (Assuming the axiom of countable choice) The union of countably many countable sets is countable.
For example, given countable sets a, b, c, ...
Using a variant of the triangular enumeration we saw above:
- a0 maps to 0
- a1 maps to 1
- b0 maps to 2
- a2 maps to 3
- b1 maps to 4
- c0 maps to 5
- a3 maps to 6
- b2 maps to 7
- c1 maps to 8
- d0 maps to 9
- a4 maps to 10
- ...
This only works if the sets a, b, c, ... are disjoint. If not, then the union is even smaller and is therefore also countable by a previous theorem.
We need the axiom of countable choice to index all the sets a, b, c, ... simultaneously.
Theorem: The set of all finite-length sequences of natural numbers is countable.
This set is the union of the length-1 sequences, the length-2 sequences, the length-3 sequences, each of which is a countable set (finite Cartesian product). So we are talking about a countable union of countable sets, which is countable by the previous theorem.
Theorem: The set of all finite subsets of the natural numbers is countable.
The elements of any finite subset can be ordered into a finite sequence. There are only countably many finite sequences, so also there are only countably many finite subsets.
Theorem: Let S and T be sets.
- If the function f : S → T is injective and T is countable then S is countable.
- If the function g : S → T is surjective and S is countable then T is countable.
These follow from the definitions of countable set as injective / surjective functions.
Cantor's theorem asserts that if A is a set and P(A) is its power set, i.e. the set of all subsets of A, then there is no surjective function from A to P(A). A proof is given in the article Cantor's theorem. As an immediate consequence of this and the Basic Theorem above we have:
Proposition: The set P(N) is not countable; i.e. it is uncountable.
The set of real numbers is uncountable, and so is the set of all infinite sequences of natural numbers.
Total orders
Countable sets can be totally ordered in various ways, for example:
- Well-orders (see also ordinal number):
- The usual order of natural numbers (0, 1, 2, 3, 4, 5, ...)
- The integers in the order (0, 1, 2, 3, ...; −1, −2, −3, ...)
- Other (not well orders):
- The usual order of integers (..., −3, −2, −1, 0, 1, 2, 3, ...)
- The usual order of rational numbers (Cannot be explicitly written as an ordered list!)
In both examples of well orders here, any subset has a least element; and in both examples of non-well orders, some subsets do not have a least element. This is the key definition that determines whether a total order is also a well order.
Licensing
Content obtained and/or adapted from:
- Countable set, Wikipedia under a CC BY-SA license