Difference between revisions of "Area between Curves"
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | * [https://www.youtube.com/watch?v=de-0e0nYf5I Determining Area Between Two Curves] by James Sousa, Math is Power 4U | + | ==Introduction== |
| − | + | Finding the area between two curves, usually given by two explicit functions, is often useful in calculus. | |
| − | + | ||
| − | + | In general the rule for finding the area between two curves is | |
| − | + | ||
| − | + | <math>A=A_{\rm top}-A_{\rm bottom}</math> or | |
| − | + | ||
| − | + | If f(x) is the upper function and g(x) is the lower function | |
| − | + | ||
| − | + | <math>A=\int\limits_a^b \bigl(f(x)-g(x)\bigr)dx</math> | |
| + | |||
| + | This is true whether the functions are in the first quadrant or not. | ||
| + | |||
| + | ==Area between two curves== | ||
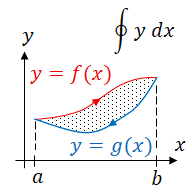
| + | Suppose we are given two functions <math>y_1=f(x)</math> and <math>y_2=g(x)</math> and we want to find the area between them on the interval <math>[a,b]</math> . Also assume that <math>f(x)\ge g(x)</math> for all <math>x</math> on the interval <math>[a,b]</math> . Begin by partitioning the interval <math>[a,b]</math> into <math>n</math> equal subintervals each having a length of <math>\Delta x=\frac{b-a}{n}</math> . Next choose any point in each subinterval, <math>x_i^*</math> . Now we can 'create' rectangles on each interval. At the point <math>x_i*</math> , the height of each rectangle is <math>f(x_i^*)-g(x_i^*)</math> and the width is <math>\Delta x</math> . Thus the area of each rectangle is <math>\bigl[f(x_i^*)-g(x_i^*)\bigr]\Delta x</math> . An ''approximation'' of the area, <math>A</math> , between the two curves is | ||
| + | :<math>A:=\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x</math> . | ||
| + | Now we take the limit as <math>n</math> approaches infinity and get | ||
| + | :<math>A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x</math> | ||
| + | which gives the exact area. Recalling the definition of the definite integral we notice that | ||
| + | :<math>A=\int\limits_a^b \bigl(f(x)-g(x)\bigr)dx</math> . | ||
| + | This formula of finding the area between two curves is sometimes known as applying integration with respect to the ''x''-axis since the rectangles used to approximate the area have their bases lying parallel to the ''x''-axis. It will be most useful when the two functions are of the form <math>y_1=f(x)</math> and <math>y_2=g(x)</math> . Sometimes however, one may find it simpler to integrate with respect to the ''y''-axis. This occurs when integrating with respect to the ''x''-axis would result in more than one integral to be evaluated. These functions take the form <math>x_1=f(y)</math> and <math>x_2=g(y)</math> on the interval <math>[c,d]</math> . Note that <math>[c,d]</math> are values of <math>y</math> . The derivation of this case is completely identical. Similar to before, we will assume that <math>f(y)\ge g(y)</math> for all <math>y</math> on <math>[c,d]</math> . Now, as before we can divide the interval into <math>n</math> subintervals and create rectangles to approximate the area between <math>f(y)</math> and <math>g(y)</math> . It may be useful to picture each rectangle having their 'width', <math>\Delta y</math> , parallel to the ''y''-axis and 'height', <math>f(y_i^*)-g(y_i^*)</math> at the point <math>y_i^*</math>, parallel to the ''x''-axis. Following from the work above we may reason that an ''approximation'' of the area, <math>A</math> , between the two curves is | ||
| + | :<math>A:=\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y</math> . | ||
| + | As before, we take the limit as <math>n</math> approaches infinity to arrive at | ||
| + | :<math>A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y</math> , | ||
| + | which is nothing more than a definite integral, so | ||
| + | :<math>A=\int\limits_c^d \bigl(f(y)-g(y)\bigr)dy</math> . | ||
| + | Regardless of the form of the functions, we basically use the same formula. | ||
| + | |||
| + | [[File:Closed path integral defined.png|Closed_path_integral_defined]] | ||
| + | |||
| + | ==Resources== | ||
| + | * [https://en.wikibooks.org/w/index.php?title=Calculus/Area&stable=1 Area], WikiBooks: Calculus | ||
| + | |||
| + | ===Videos=== | ||
| + | [https://www.youtube.com/watch?v=de-0e0nYf5I Determining Area Between Two Curves] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=E_1aDcOoDtE The Area Between Two Graphs] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=q7De3oOp4Ug Ex 1: Area Between a Linear and Quadratic Function (respect to x)] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=n2JqTztMrvQ Ex 2: Area Between a Linear and Exponential Function (respect to x)] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=OqMbRAEQ-cg Ex 3: Area Between Two Exponential Functions (respect to x)] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=58Esio4q4jk Ex 4: Area Between Two Quadratic Functions (respect to x)] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=CPhUolqwLNk Ex 1: Area Bounded by Two Functions] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=lskEXsJaJV0 Ex 2: Area Bounded by Two Functions (Two Regions)] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=BH-V6Gx2n8E Ex 3: Area Bounded by Two Trig. Functions] by James Sousa, Math is Power 4U | ||
| + | |||
| + | [https://www.youtube.com/watch?v=N4fEuEQLG5c Ex: Determine a Function Given the Area Between Two Functions] by James Sousa, Math is Power 4U | ||
[https://youtu.be/DRFyNHdVgUA Finding Areas Between Curves] by patrickJMT | [https://youtu.be/DRFyNHdVgUA Finding Areas Between Curves] by patrickJMT | ||
| Line 41: | Line 84: | ||
[https://youtu.be/wXMr2YYDMiM Area Between Two Curves & Under Curve - Respect to y & x] by The Organic Chemistry Tutor | [https://youtu.be/wXMr2YYDMiM Area Between Two Curves & Under Curve - Respect to y & x] by The Organic Chemistry Tutor | ||
| + | |||
| + | ==Licensing== | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Area Area, Wikibooks: Calculus] under a CC BY-SA license | ||
Latest revision as of 10:41, 29 October 2021
Introduction
Finding the area between two curves, usually given by two explicit functions, is often useful in calculus.
In general the rule for finding the area between two curves is
or
If f(x) is the upper function and g(x) is the lower function
This is true whether the functions are in the first quadrant or not.
Area between two curves
Suppose we are given two functions and and we want to find the area between them on the interval . Also assume that for all on the interval . Begin by partitioning the interval into equal subintervals each having a length of . Next choose any point in each subinterval, . Now we can 'create' rectangles on each interval. At the point , the height of each rectangle is and the width is . Thus the area of each rectangle is . An approximation of the area, , between the two curves is
- .
Now we take the limit as approaches infinity and get
which gives the exact area. Recalling the definition of the definite integral we notice that
- .
This formula of finding the area between two curves is sometimes known as applying integration with respect to the x-axis since the rectangles used to approximate the area have their bases lying parallel to the x-axis. It will be most useful when the two functions are of the form and . Sometimes however, one may find it simpler to integrate with respect to the y-axis. This occurs when integrating with respect to the x-axis would result in more than one integral to be evaluated. These functions take the form and on the interval . Note that are values of . The derivation of this case is completely identical. Similar to before, we will assume that for all on . Now, as before we can divide the interval into subintervals and create rectangles to approximate the area between and . It may be useful to picture each rectangle having their 'width', , parallel to the y-axis and 'height', at the point , parallel to the x-axis. Following from the work above we may reason that an approximation of the area, , between the two curves is
- .
As before, we take the limit as approaches infinity to arrive at
- ,
which is nothing more than a definite integral, so
- .
Regardless of the form of the functions, we basically use the same formula.
Resources
- Area, WikiBooks: Calculus
Videos
Determining Area Between Two Curves by James Sousa, Math is Power 4U
The Area Between Two Graphs by James Sousa, Math is Power 4U
Ex 1: Area Between a Linear and Quadratic Function (respect to x) by James Sousa, Math is Power 4U
Ex 2: Area Between a Linear and Exponential Function (respect to x) by James Sousa, Math is Power 4U
Ex 3: Area Between Two Exponential Functions (respect to x) by James Sousa, Math is Power 4U
Ex 4: Area Between Two Quadratic Functions (respect to x) by James Sousa, Math is Power 4U
Ex 1: Area Bounded by Two Functions by James Sousa, Math is Power 4U
Ex 2: Area Bounded by Two Functions (Two Regions) by James Sousa, Math is Power 4U
Ex 3: Area Bounded by Two Trig. Functions by James Sousa, Math is Power 4U
Ex: Determine a Function Given the Area Between Two Functions by James Sousa, Math is Power 4U
Finding Areas Between Curves by patrickJMT
Areas Between Curves - 2 Regions by patrickJMT
Finding Area by Integrating with Respect to y by patrickJMT
Area Between Curves - Integrating with Respect to y by patrickJMT
Area Between Curves - Integrating with Respect to y - Part 2 by patrickJMT
Finding Areas Between Curve: Region and Functions Given by patrickJMT
Area of a Region Bounded by 3 Curves by patrickJMT
Area between curves... which curve is which? by Krista King
Area between curves - dx by Krista King
Area between curves - dy by Krista King
Area between curves - sketching by Krista King
Area Between Curves Example 1 by Krista King
Area Between Curves Example 2 by Krista King
Area Between Curves Example 3 by Krista King
Area Between Two Curves by The Organic Chemistry Tutor
Area Between Two Curves & Under Curve - Respect to y & x by The Organic Chemistry Tutor
Licensing
Content obtained and/or adapted from:
- Area, Wikibooks: Calculus under a CC BY-SA license




![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)








![{\displaystyle {\bigl [}f(x_{i}^{*})-g(x_{i}^{*}){\bigr ]}\Delta x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3efcbd6878b1c9c84285d7123766c63013ad35fe)

![{\displaystyle A:=\sum _{i=1}^{n}{\Big [}f(x_{i}^{*})-g(x_{i}^{*}){\Big ]}\Delta x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b532cb175e18edf6dc343ec2abc5acbf183415b7)
![{\displaystyle A=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big [}f(x_{i}^{*})-g(x_{i}^{*}){\Big ]}\Delta x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f6dd23a75bdf922a3a92f28772310ab80f2805)


![{\displaystyle [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)







![{\displaystyle A:=\sum _{i=1}^{n}{\Big [}f(y_{i}^{*})-g(y_{i}^{*}){\Big ]}\Delta y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8670a382efc3d742ae073ca7fc9f2f77fda78423)
![{\displaystyle A=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big [}f(y_{i}^{*})-g(y_{i}^{*}){\Big ]}\Delta y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9682357a788e80bae02a003b2ac2a10beb6bbc1a)