Difference between revisions of "Applications of Integrals"
(Created page with " * Average value of a function * Area between curves * Distance, velocity, acceleration * Volume * Work * Arc length * Surface area * Center of mass * Hydrostatic pressure and...") |
|||
| Line 1: | Line 1: | ||
| + | ==Area between two curves== | ||
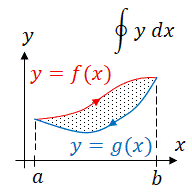
| + | Suppose we are given two functions <math>y_1=f(x)</math> and <math>y_2=g(x)</math> and we want to find the area between them on the interval <math>[a,b]</math> . Also assume that <math>f(x)\ge g(x)</math> for all <math>x</math> on the interval <math>[a,b]</math> . Begin by partitioning the interval <math>[a,b]</math> into <math>n</math> equal subintervals each having a length of <math>\Delta x=\frac{b-a}{n}</math> . Next choose any point in each subinterval, <math>x_i^*</math> . Now we can 'create' rectangles on each interval. At the point <math>x_i*</math> , the height of each rectangle is <math>f(x_i^*)-g(x_i^*)</math> and the width is <math>\Delta x</math> . Thus the area of each rectangle is <math>\bigl[f(x_i^*)-g(x_i^*)\bigr]\Delta x</math> . An ''approximation'' of the area, <math>A</math> , between the two curves is | ||
| + | :<math>A:=\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x</math> . | ||
| + | Now we take the limit as <math>n</math> approaches infinity and get | ||
| + | :<math>A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x</math> | ||
| + | which gives the exact area. Recalling the definition of the definite integral we notice that | ||
| + | :<math>A=\int\limits_a^b \bigl(f(x)-g(x)\bigr)dx</math> . | ||
| + | This formula of finding the area between two curves is sometimes known as applying integration with respect to the ''x''-axis since the rectangles used to approximate the area have their bases lying parallel to the ''x''-axis. It will be most useful when the two functions are of the form <math>y_1=f(x)</math> and <math>y_2=g(x)</math> . Sometimes however, one may find it simpler to integrate with respect to the ''y''-axis. This occurs when integrating with respect to the ''x''-axis would result in more than one integral to be evaluated. These functions take the form <math>x_1=f(y)</math> and <math>x_2=g(y)</math> on the interval <math>[c,d]</math> . Note that <math>[c,d]</math> are values of <math>y</math> . The derivation of this case is completely identical. Similar to before, we will assume that <math>f(y)\ge g(y)</math> for all <math>y</math> on <math>[c,d]</math> . Now, as before we can divide the interval into <math>n</math> subintervals and create rectangles to approximate the area between <math>f(y)</math> and <math>g(y)</math> . It may be useful to picture each rectangle having their 'width', <math>\Delta y</math> , parallel to the ''y''-axis and 'height', <math>f(y_i^*)-g(y_i^*)</math> at the point <math>y_i^*</math>, parallel to the ''x''-axis. Following from the work above we may reason that an ''approximation'' of the area, <math>A</math> , between the two curves is | ||
| + | :<math>A:=\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y</math> . | ||
| + | As before, we take the limit as <math>n</math> approaches infinity to arrive at | ||
| + | :<math>A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y</math> , | ||
| + | which is nothing more than a definite integral, so | ||
| + | :<math>A=\int\limits_c^d \bigl(f(y)-g(y)\bigr)dy</math> . | ||
| + | Regardless of the form of the functions, we basically use the same formula. | ||
| − | + | [[File:Closed path integral defined.png|Closed_path_integral_defined]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Resources== | ==Resources== | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Area Area], Wikibooks: Calculus | ||
* [https://tutorial.math.lamar.edu/classes/calci/intappsintro.aspx Applications of Integrals - Cal I], Paul's Online Notes | * [https://tutorial.math.lamar.edu/classes/calci/intappsintro.aspx Applications of Integrals - Cal I], Paul's Online Notes | ||
* [https://tutorial.math.lamar.edu/classes/calcii/intappsintro.aspx Applications of Integrals - Cal II], Paul's Online Notes | * [https://tutorial.math.lamar.edu/classes/calcii/intappsintro.aspx Applications of Integrals - Cal II], Paul's Online Notes | ||
Revision as of 14:01, 15 October 2021
Area between two curves
Suppose we are given two functions and and we want to find the area between them on the interval . Also assume that for all on the interval . Begin by partitioning the interval into equal subintervals each having a length of . Next choose any point in each subinterval, . Now we can 'create' rectangles on each interval. At the point , the height of each rectangle is and the width is . Thus the area of each rectangle is . An approximation of the area, , between the two curves is
- .
Now we take the limit as approaches infinity and get
which gives the exact area. Recalling the definition of the definite integral we notice that
- .
This formula of finding the area between two curves is sometimes known as applying integration with respect to the x-axis since the rectangles used to approximate the area have their bases lying parallel to the x-axis. It will be most useful when the two functions are of the form and . Sometimes however, one may find it simpler to integrate with respect to the y-axis. This occurs when integrating with respect to the x-axis would result in more than one integral to be evaluated. These functions take the form and on the interval . Note that are values of . The derivation of this case is completely identical. Similar to before, we will assume that for all on . Now, as before we can divide the interval into subintervals and create rectangles to approximate the area between and . It may be useful to picture each rectangle having their 'width', , parallel to the y-axis and 'height', at the point , parallel to the x-axis. Following from the work above we may reason that an approximation of the area, , between the two curves is
- .
As before, we take the limit as approaches infinity to arrive at
- ,
which is nothing more than a definite integral, so
- .
Regardless of the form of the functions, we basically use the same formula.
Resources
- Area, Wikibooks: Calculus
- Applications of Integrals - Cal I, Paul's Online Notes
- Applications of Integrals - Cal II, Paul's Online Notes


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)








![{\displaystyle {\bigl [}f(x_{i}^{*})-g(x_{i}^{*}){\bigr ]}\Delta x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3efcbd6878b1c9c84285d7123766c63013ad35fe)

![{\displaystyle A:=\sum _{i=1}^{n}{\Big [}f(x_{i}^{*})-g(x_{i}^{*}){\Big ]}\Delta x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b532cb175e18edf6dc343ec2abc5acbf183415b7)
![{\displaystyle A=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big [}f(x_{i}^{*})-g(x_{i}^{*}){\Big ]}\Delta x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f6dd23a75bdf922a3a92f28772310ab80f2805)



![{\displaystyle [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)







![{\displaystyle A:=\sum _{i=1}^{n}{\Big [}f(y_{i}^{*})-g(y_{i}^{*}){\Big ]}\Delta y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8670a382efc3d742ae073ca7fc9f2f77fda78423)
![{\displaystyle A=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big [}f(y_{i}^{*})-g(y_{i}^{*}){\Big ]}\Delta y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9682357a788e80bae02a003b2ac2a10beb6bbc1a)