Difference between revisions of "Graphs of Polynomials"
| Line 1: | Line 1: | ||
<div class="floatright"> | <div class="floatright"> | ||
<gallery perrow="2" widths="200px" heights="200px"> | <gallery perrow="2" widths="200px" heights="200px"> | ||
| − | File:Algebra1 fnz fig037 pc.svg|Polynomial of degree 0:<br/><small>{{math|''f''(''x'') | + | File:Algebra1 fnz fig037 pc.svg|Polynomial of degree 0:<br/><small>{{math|''f''(''x'') = 2}}</small> |
| − | File:Fonction de Sophie Germain.png|Polynomial of degree 1:<br/><small>{{math|''f''(''x'') | + | File:Fonction de Sophie Germain.png|Polynomial of degree 1:<br/><small>{{math|''f''(''x'') = 2''x'' + 1}}</small> |
| − | File:Polynomialdeg2.svg|Polynomial of degree 2:<br/><small>{{math|''f''(''x'') | + | File:Polynomialdeg2.svg|Polynomial of degree 2:<br/><small>{{math|''f''(''x'') = ''x''<sup>2</sup> − ''x'' − 2}}<br/>{{math|= (''x'' + 1)(''x'' − 2)}}</small> |
| − | File:Polynomialdeg3.svg|Polynomial of degree 3:<br/><small>{{math|''f''(''x'') | + | File:Polynomialdeg3.svg|Polynomial of degree 3:<br/><small>{{math|''f''(''x'') = ''x''<sup>3</sup>/4 + 3''x''<sup>2</sup>/4 − 3''x''/2 − 2}}<br/>{{math|= 1/4 (''x'' + 4)(''x'' + 1)(''x'' − 2)}}</small> |
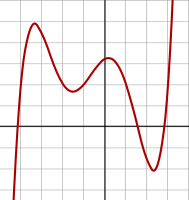
| − | File:Polynomialdeg4.svg|Polynomial of degree 4:<br/><small>{{math|''f''(''x'') | + | File:Polynomialdeg4.svg|Polynomial of degree 4:<br/><small>{{math|''f''(''x'') = 1/14 (''x'' + 4)(''x'' + 1)(''x'' − 1)(''x'' − 3) <br/>+ 0.5}}</small> |
| − | File:Quintic polynomial.svg|Polynomial of degree 5:<br/><small>{{math|''f''(''x'') | + | File:Quintic polynomial.svg|Polynomial of degree 5:<br/><small>{{math|''f''(''x'') = 1/20 (''x'' + 4)(''x'' + 2)(''x'' + 1)(''x'' − 1)<br/>(''x'' − 3) + 2}}</small> |
| − | File:Sextic Graph.svg|Polynomial of degree 6:<br/><small>{{math|''f''(''x'') | + | File:Sextic Graph.svg|Polynomial of degree 6:<br/><small>{{math|''f''(''x'') = 1/100 (''x''<sup>6</sup> − 2''x'' <sup>5</sup> − 26''x''<sup>4</sup> + 28''x''<sup>3</sup>}}<br/>{{math|+ 145''x''<sup>2</sup> − 26''x'' − 80)}}</small> |
| − | File:Septic graph.svg|Polynomial of degree 7:<br/><small>{{math|''f''(''x'') | + | File:Septic graph.svg|Polynomial of degree 7:<br/><small>{{math|''f''(''x'') = (''x'' − 3)(''x'' − 2)(''x'' − 1)(''x'')(''x'' + 1)(''x'' + 2)}}<br/>{{math|(''x'' + 3)}}</small> |
</gallery> | </gallery> | ||
</div> | </div> | ||
| Line 58: | Line 58: | ||
Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior. | Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior. | ||
| + | |||
| + | ==Resources== | ||
| + | * [https://en.wikipedia.org/wiki/Polynomial Polynomial], Wikipedia | ||
| + | |||
| + | |||
| + | == Licensing == | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikipedia.org/wiki/Polynomial Polynomial, Wikipedia] under a CC BY-SA license | ||
Revision as of 13:30, 21 October 2021
A polynomial function is a function that can be defined by evaluating a polynomial. More precisely, a function f of one argument from a given domain is a polynomial function if there exists a polynomial
that evaluates to for all x in the domain of f (here, n is a non-negative integer and a0, a1, a2, ..., an are constant coefficients). Generally, unless otherwise specified, polynomial functions have complex coefficients, arguments, and values. In particular, a polynomial, restricted to have real coefficients, defines a function from the complex numbers to the complex numbers. If the domain of this function is also restricted to the reals, the resulting function is a real function that maps reals to reals.
For example, the function f, defined by
is a polynomial function of one variable. Polynomial functions of several variables are similarly defined, using polynomials in more than one indeterminate, as in
According to the definition of polynomial functions, there may be expressions that obviously are not polynomials but nevertheless define polynomial functions. An example is the expression which takes the same values as the polynomial on the interval , and thus both expressions define the same polynomial function on this interval.
Every polynomial function is continuous, smooth, and entire.
Graphs
A polynomial function in one real variable can be represented by a graph.
- The graph of the zero polynomial Template:Block indent is the x-axis.
- The graph of a degree 0 polynomial Template:Block indent is a horizontal line with Template:Nowrap
- The graph of a degree 1 polynomial (or linear function) Template:Block indent is an oblique line with Template:Nowrap and slope a1.
- The graph of a degree 2 polynomial Template:Block indent is a parabola.
- The graph of a degree 3 polynomial Template:Block indent is a cubic curve.
- The graph of any polynomial with degree 2 or greater Template:Block indent is a continuous non-linear curve.
A non-constant polynomial function tends to infinity when the variable increases indefinitely (in absolute value). If the degree is higher than one, the graph does not have any asymptote. It has two parabolic branches with vertical direction (one branch for positive x and one for negative x).
Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior.
Resources
- Polynomial, Wikipedia
Licensing
Content obtained and/or adapted from:
- Polynomial, Wikipedia under a CC BY-SA license













![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)