Difference between revisions of "Convergent Sequences in Metric Spaces"
(Created page with "===Limits of Sequences in Metric Spaces=== <p>Recall that if a sequence of real numbers <span class="math-inline"><math>(x_n)_{n=1}^{\infty} = (x_1, x_2, ..., x_n, ...)</math>...") |
|||
| Line 10: | Line 10: | ||
</blockquote> | </blockquote> | ||
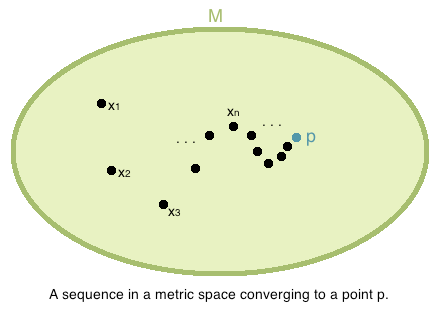
<p><em>There is a subtle but important point to make. In the definition above, <span class="math-inline"><math>\lim_{n \to \infty} x_n = p</math></span> represents the limit of a sequence of elements from the metric space <span class="math-inline"><math>(M,d)</math></span> to an element <span class="math-inline"><math>p \in M</math></span> while <span class="math-inline"><math>\lim_{n \to \infty} d(x_n, p) = 0</math></span> represents the limit of a sequence of positive real numbers to <span class="math-inline"><math>0</math></span> - such limits we already have experience with.</em></p> | <p><em>There is a subtle but important point to make. In the definition above, <span class="math-inline"><math>\lim_{n \to \infty} x_n = p</math></span> represents the limit of a sequence of elements from the metric space <span class="math-inline"><math>(M,d)</math></span> to an element <span class="math-inline"><math>p \in M</math></span> while <span class="math-inline"><math>\lim_{n \to \infty} d(x_n, p) = 0</math></span> represents the limit of a sequence of positive real numbers to <span class="math-inline"><math>0</math></span> - such limits we already have experience with.</em></p> | ||
| − | + | ||
| + | [[File:Convergent sequence in metric space.png|center|Convergent sequence in metric space]] | ||
| + | |||
<p>For example, if <span class="math-inline"><math>M</math></span> is any nonempty set, <span class="math-inline"><math>d : M \times M \to [0, \infty)</math></span> is the discrete metric, and <span class="math-inline"><math>x \in M</math></span>, then the sequence defined by <span class="math-inline"><math>x_n = x</math></span> for all <span class="math-inline"><math>n \in \{ 1, 2, ... \}</math></span>, then the sequence:</p> | <p>For example, if <span class="math-inline"><math>M</math></span> is any nonempty set, <span class="math-inline"><math>d : M \times M \to [0, \infty)</math></span> is the discrete metric, and <span class="math-inline"><math>x \in M</math></span>, then the sequence defined by <span class="math-inline"><math>x_n = x</math></span> for all <span class="math-inline"><math>n \in \{ 1, 2, ... \}</math></span>, then the sequence:</p> | ||
Revision as of 10:42, 8 November 2021
Limits of Sequences in Metric Spaces
Recall that if a sequence of real numbers is an infinite ordered list where for every . We will now generalize the concept of a sequence to contain elements from a metric space .
Definition: Let be a metric space. An (infinite) Sequence in denoted is an infinite ordered list of elements for all .
Finite sequences in a metric space can be defined as a finite ordered list of elements in but their study is not that interesting to us.
We can also define whether a sequence of elements from a metric space converges or diverges.
Definition: Let be a metric space. A sequence in is said to be Convergent to the element written if and the element is said to be the Limit of the sequence . If no such exists, then is said to be Divergent.
There is a subtle but important point to make. In the definition above, represents the limit of a sequence of elements from the metric space to an element while represents the limit of a sequence of positive real numbers to - such limits we already have experience with.
For example, if is any nonempty set, is the discrete metric, and , then the sequence defined by for all , then the sequence:
Furthermore, it's not hard to see that this sequence converges to , i.e., , i.e., since for all we have that , so .
We will soon see that many of theorems regarding limits of sequences of real numbers are analogous to limits of sequences of elements from metric spaces.