Convergent Sequences in Metric Spaces

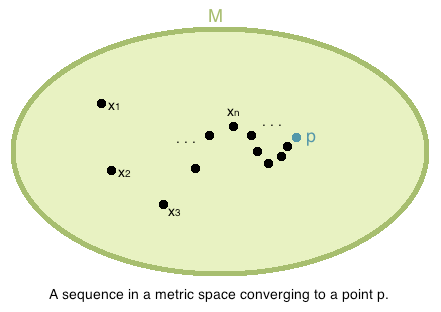
Limits of Sequences in Metric Spaces

Recall that if a sequence of real numbers $(x_{n})_{n=1}^{\infty }=(x_{1},x_{2},...,x_{n},...)$ is an infinite ordered list where $x_{k}\in \mathbb {R}$ for every $k\in \{1,2,...\}$. We will now generalize the concept of a sequence to contain elements from a metric space $(M,d)$.

Definition: Let $(M,d)$ be a metric space. An (infinite) Sequence in $M$ denoted $(x_{n})_{n=1}^{\infty }=(x_{1},x_{2},...,x_{n},...)$ is an infinite ordered list of elements $x_{k}\in M$ for all $k\in \{1,2,...\}$.

Finite sequences in a metric space can be defined as a finite ordered list of elements in $M$ but their study is not that interesting to us.

We can also define whether a sequence $(x_{n})_{n=1}^{\infty }$ of elements from a metric space $(M,d)$ converges or diverges.

Definition: Let $(M,d)$ be a metric space. A sequence $(x_{n})_{n=1}^{\infty }$ in $M$ is said to be Convergent to the element $p\in M$ written $\lim _{n\to \infty }x_{n}=p$ if $\lim _{n\to \infty }d(x_{n},p)=0$ and the element $p$ is said to be the Limit of the sequence $(x_{n})_{n=1}^{\infty }$. If no such $p\in M$ exists, then $(x_{n})_{n=1}^{\infty }$ is said to be Divergent.

There is a subtle but important point to make. In the definition above, $\lim _{n\to \infty }x_{n}=p$ represents the limit of a sequence of elements from the metric space $(M,d)$ to an element $p\in M$ while $\lim _{n\to \infty }d(x_{n},p)=0$ represents the limit of a sequence of positive real numbers to $0$ - such limits we already have experience with.

For example, if $M$ is any nonempty set, $d:M\times M\to [0,\infty )$ is the discrete metric, and $x\in M$, then the sequence defined by $x_{n}=x$ for all $n\in \{1,2,...\}$, then the sequence:

${\begin{aligned}\quad (x_{n})_{n=1}^{\infty }=(x)_{n=1}^{\infty }=(x,x,...,x,...)\end{aligned}}$

Furthermore, it's not hard to see that this sequence converges to $x$, i.e., $\lim _{n\to \infty }x_{n}=x$, i.e., $\lim _{n\to \infty }d(x_{n},x)=0$ since for all $x_{n}$ we have that $d(x_{n},x)=0$, so $\lim _{n\to \infty }d(x_{n},x)=\lim _{n\to \infty }0=0$.

We will soon see that many of theorems regarding limits of sequences of real numbers are analogous to limits of sequences of elements from metric spaces.

The Boundedness of Convergent Sequences in Metric Spaces

If $(M,d)$ is a metric space and $(x_{n})_{n=1}^{\infty }$ is a sequence in $M$ that is convergent then the limit of this sequence $p\in M$ is unique.

We will now look at another rather nice theorem which states that if $(x_{n})_{n=1}^{\infty }$ is convergent then it is also bounded.

Theorem 1: Let $(M,d)$ be a metric space and let $(x_{n})_{n=1}^{\infty }$ be a sequence in $M$. If $(x_{n})_{n=1}^{\infty }$ is convergent then the set $\{x_{1},x_{2},...,x_{n},...\}$ is bounded.

• Proof: Let $(M,d)$ be a metric space and let $(x_{n})_{n=1}^{\infty }$ be a sequence in $M$ that converges to $p\in M$, i.e., $\lim _{n\to \infty }x_{n}=p$. Then $\lim _{n\to \infty }d(x_{n},p)=0$. So for all $\epsilon >0$ there exists an $N\in \mathbb {N}$ such that if $n\geq N$ then $d(x_{n},p)<\epsilon$. So for $\epsilon _{0}=1>0$ there exists an $N(\epsilon _{0})\in \mathbb {N}$ such that if $n\geq N(\epsilon _{0})$ then:

${\begin{aligned}\quad d(x_{n},p)<\epsilon _{0}=1\end{aligned}}$

• Now consider the elements $x_{1},x_{2},...,x_{N(\epsilon _{0})}$. This is a finite set of elements and furthermore the set of distances from these elements to $p$ is finite:

${\begin{aligned}\quad \{d(x_{1},p),d(x_{2},p),...,d(x_{N(\epsilon _{0})-1},p)\}\end{aligned}}$

• Define $M^{*}$ to be the maximum of these distances:

${\begin{aligned}\quad M^{*}=\max\{d(x_{1},p),d(x_{2},p),...,d(x_{N(\epsilon _{0})-1},p)\}\end{aligned}}$

• So if $1\leq n<N(\epsilon _{0})$ we have that $d(x_{n},p)\leq M^{*}$ and if $n\geq N(\epsilon _{0})$ then $d(x_{n},p)<1$. Let $M=\max\{M^{*},1\}$. Then for all $n\in \mathbb {N}$, $d(x_{n},p)\leq M$. So consider the open ball $B(p,M+1)$. Then $x_{n}\in B(p,M+1)$ for all $n\in \{1,2,...\}$ so:

${\begin{aligned}\quad \{x_{1},x_{2},...,x_{n},...\}\subseteq B(p,M+1)\end{aligned}}$

• Therefore $\{x_{1},x_{2},...,x_{n},...\}$ is a bounded set in $M$. $\blacksquare$

Licensing

Content obtained and/or adapted from:

• Limits of Sequences in Metric Spaces, mathonline.wikidot.com under a CC BY-SA license
• The Boundedness of Convergent Sequences in Metric Spaces, mathonline.wikidot.com under a CC BY-SA license