Difference between revisions of "Trigonometric Substitution"

From Department of Mathematics at UTSA
Jump to navigation Jump to search
(Added video links)
 
Line 1: Line 1:
−
[https://youtu.be/BVn8x7wCa3A Ex 1: Integration Using Trigonometric Substitution] by James Sousa
+
The idea behind the trigonometric substitution is quite simple: to replace expressions involving square roots with expressions that involve standard trigonometric functions, but ''no square roots''. Integrals involving trigonometric functions are often easier to solve than integrals involving square roots.
  
−
[https://youtu.be/a-f63vZVuBQ Ex 2: Integration Using Trigonometric Substitution] by James Sousa
+
Let us demonstrate this idea in practice. Consider the expression <math>\sqrt{1-x^2}</math> . Probably the most basic trigonometric identity is <math>\sin^2(\theta)+\cos^2(\theta)=1</math> for an arbitrary angle <math>\theta</math> . If we replace <math>x</math> in this expression by <math>\sin(\theta)</math> , with the help of this trigonometric identity we see
 +
:<math>\sqrt{1-x^2}=\sqrt{1-\sin^2(\theta)}=\sqrt{\cos^2(\theta)}=\cos(\theta)</math>
 +
Note that we could write <math>\theta=\arcsin(x)</math> since we replaced <math>x^2</math> with <math>\sin^2(\theta)</math> .
  
−
[https://youtu.be/jZa4FM6l6pM Ex 3: Integration Using Trigonometric Substitution] by James Sousa
+
We would like to mention that technically one should write the absolute value of <math>\cos(\theta)</math> , in other words <math>\bigl|\cos(\theta)\bigr|</math> as our final answer since <math>\sqrt{a^2}=|a|</math> for all possible <math>a</math> . But as long as we are careful about the domain of all possible <math>x</math> and how <math>\cos(\theta)</math> is used in the final computation, omitting the absolute value signs does not constitute a problem. However, we cannot directly interchange the simple expression <math>\cos(\theta)</math> with the complicated <math>\sqrt{1-x^2}</math> wherever it may appear, we must remember when integrating by substitution we need to take the derivative into account. That is we need to remember that <math>dx=\cos(\theta)d\theta</math> , and to get a integral that only involves <math>\theta</math> we need to also replace <math>dx</math> by something in terms of <math>d\theta</math> . Thus, if we see an
 +
integral of the form
 +
:<math>\int\sqrt{1-x^2}dx</math>
 +
we can rewrite it as
 +
:<math>\int\cos(\theta)\cos(\theta)d\theta=\int\cos^2(\theta)d\theta</math>
 +
Notice in the expression on the left that the first <math>\cos(\theta)</math> comes from replacing the <math>\sqrt{1-x^2}</math> and the <math>\cos(\theta)d\theta</math> comes from substituting for the <math>dx</math> . 
  
−
[https://youtu.be/ObxsrPx44nw Ex 4: Integration Using Trigonometric Substitution] by James Sousa
+
Since <math>\cos^2(\theta)=\frac{1+\cos(2\theta)}{2}</math> our original integral reduces to:
 +
:<math>\tfrac12\int d\theta+\tfrac12\int\cos(2\theta)d\theta</math> .
  
−
[https://youtu.be/OnT7Ub68FWg Ex 5: Integration Using Trigonometric Substitution] by James Sousa
+
These last two integrals are easily handled. For the first integral we get
 +
:<math>\tfrac12\int d\theta=\tfrac12\theta</math>
  
−
[https://youtu.be/3lC5AuCFK4c Trigonometric Substitution - Example 1] by patrickJMT
+
For the second integral we do a substitution, namely <math>u=2\theta,du=2d\theta</math> to get:
 +
:<math>\tfrac12\int\cos(2\theta)d\theta=\tfrac12\int\cos(u)\tfrac12du=\tfrac14\sin(u)=\frac{\sin(2\theta)}{4}</math>
  
−
[https://youtu.be/GVL4lHX6DgM Trigonometric Substitution - Example 2] by patrickJMT
+
Finally we see that:  
 +
:<math>\int\cos^2(\theta)d\theta=\frac{\theta}{2}+\frac{\sin(2\theta)}{4}=\frac{\theta+\sin(\theta)\cos(\theta)}{2}</math>
 +
However, this is in terms of <math>\theta</math> and not in terms of <math>x</math> , so we must substitute back in order to rewrite the answer in terms of <math>x</math> .
  
−
[https://youtu.be/yW6Odu0YHL0 Trigonometric Substitution - Example 3 Part 1] by patrickJMT
+
That is we worked out that:  
 +
:<math>\sin(\theta)=x\qquad\cos(\theta)=\sqrt{1-x^2}\qquad\theta=\arcsin(x)</math>
  
−
[https://youtu.be/4QNntd_KZbc Trigonometric Substitution - Example 4 Rational Powers] by patrickJMT
+
So we arrive at our final answer
 +
:<math>\int\sqrt{1-x^2}dx=\frac{\arcsin(x)+x\sqrt{1-x^2}}{2}</math>
  
−
[https://youtu.be/wuRNmNDLanc Trigonometric Substitution More Examples] by patrickJMT
+
As you can see, even for a fairly harmless looking integral this technique can involve quite a lot of calculation. Often it is helpful to see if a simpler method will suffice before turning to trigonometric substitution. On the other hand, frequently in the case of integrands involving square roots, this is the most tractable way to solve the problem. We begin with giving some rules of thumb to help you decide which trigonometric substitutions might be helpful.
 +
 
 +
If the integrand contains a single factor of one of the forms <math>\sqrt{a^2-x^2}\mbox{ or }\sqrt{a^2+x^2}\mbox{ or }\sqrt{x^2-a^2}</math> we can try a trigonometric substitution.
 +
 
 +
<blockquote style="background: white; border: 1px solid black; padding: 1em;">
 +
*If the integrand contains <math>\sqrt{a^2-x^2}</math> let <math>x=a\sin(\theta)</math> and use the identity <math>1-\sin^2(\theta)=\cos^2(\theta)</math> .
 +
*If the integrand contains <math>\sqrt{a^2+x^2}</math> let <math>x=a\tan(\theta)</math> and use the identity <math>1+\tan^2(\theta)=\sec^2(\theta)</math> .
 +
*If the integrand contains <math>\sqrt{x^2-a^2}</math> let <math>x=a\sec(\theta)</math> and use the identity <math>\sec^2(\theta)-1=\tan^2(\theta)</math> .
 +
</blockquote>
 +
[[Image:Wikiversity-logo-Snorky.svg|right|thumb|80px|[[V:Trigonometric Substitutions|Trigonometric Substitutions]]]]
 +
[[Image:Wikipedia-logo-en.png‎‎|right|thumb|80px|[[W:Trigonometric substitution|Trigonometric Substitutions]]]]
 +
 
 +
===Sine substitution===
 +
[[Image:Trig_Sub_Triangle_1.png|frame|right|273px|This substitution is easily derived from a triangle, using the [[w:Pythagorean_Theorem|Pythagorean Theorem]].]]
 +
 
 +
If the integrand contains a piece of the form <math>\sqrt{a^2-x^2}</math> we use the substitution
 +
:<math>x=a\sin(\theta)\quad dx=a\cos(\theta)d\theta</math>
 +
This will transform the integrand to a trigonometric function. If the new integrand can't be integrated on sight then the tan-half-angle substitution described below will generally transform it into a more tractable algebraic integrand.
 +
 
 +
E.g., if the integrand is <math>\sqrt{1-x^2}</math> ,
 +
 
 +
:<math>\begin{align}
 +
\int\limits_0^1\sqrt{1-x^2}dx&=\int\limits_0^\frac{\pi}{2}\sqrt{1-\sin^2(\theta)}\cos(\theta)d\theta\\
 +
&=\int\limits_0^\frac{\pi}{2}\cos^2(\theta)d\theta\\
 +
&=\tfrac12\int\limits_0^\frac{\pi}{2}\bigl(1+\cos(2\theta)\bigr)d\theta\\
 +
&=\frac{\pi}{4}
 +
\end{align}</math>
 +
 
 +
If the integrand is <math>\sqrt{\frac{1+x}{1-x}}</math> , we can rewrite it as
 +
:<math>\sqrt{\frac{1+x}{1-x}}=\sqrt{\frac{1+x}{1+x}\cdot\frac{1+x}{1-x}}=\frac{1+x}{\sqrt{1-x^2}}</math>
 +
Then we can make the substitution
 +
 
 +
:<math>\begin{align}
 +
\int\limits_0^a\frac{1+x}{\sqrt{1-x^2}}dx&=\int\limits_0^\alpha\frac{1+\sin(\theta)}{\cos(\theta)}\cos(\theta)d\theta
 +
&0<a<1\\
 +
&=\int\limits_0^\alpha\bigl(1+\sin(\theta)\bigr)d\theta&\alpha=\arcsin(a)\\
 +
&=\alpha+\Big[-\cos(\theta)\Big]_0^\alpha\\
 +
&=\alpha+1-\cos(\alpha)\\
 +
&=1+\arcsin(a)-\sqrt{1-a^2}
 +
\end{align}</math>
 +
 
 +
===Tangent substitution===
 +
[[Image:Trig_Sub_Triangle_2.png|frame|right|273px|This substitution is easily derived from a triangle, using the [[w:Pythagorean_Theorem|Pythagorean Theorem]].]]
 +
 
 +
When the integrand contains a piece of the form
 +
<math>\sqrt{a^2+x^2}</math>
 +
we use the substitution
 +
:<math>x=a\tan(\theta)\qquad\sqrt{x^2+a^2}=a\sec(\theta)\qquad dx=a\sec^2(\theta)d\theta</math>
 +
 
 +
E.g., if the integrand is <math>(x^2+a^2)^{-\frac32}</math> then on making this substitution we find
 +
 
 +
:<math>\begin{align}
 +
\int\limits_0^z(x^2+a^2)^{-\frac32}dx&=a^{-2}\int\limits_0^\alpha \cos(\theta)d\theta&z>0\\
 +
&=a^{-2}\Big[\sin(\theta)\Big]_0^\alpha&\alpha=\arctan\left(\tfrac{z}{a}\right)\\
 +
&=a^{-2}\sin(\alpha)\\
 +
&=a^{-2}\frac{\frac{z}{a}}{\sqrt{1+\frac{z^2}{a^2}}}\\
 +
&=\frac{z}{a^2\sqrt{a^2+z^2}}
 +
\end{align}</math>
 +
 
 +
If the integral is
 +
 
 +
:<math>I=\int\limits_0^z\sqrt{x^2+a^2}\qquad z>0</math>
 +
 
 +
then on making this substitution we find
 +
 
 +
:<math>\begin{matrix}
 +
I & = & a^2 \int_0^\alpha \sec^3 \theta \, d\theta
 +
& & & \alpha = \tan^{-1} (z/a) \\
 +
& = & a^2 \int_0^\alpha \sec \theta \, d\tan \theta & & & \\
 +
& = & a^2 [ \sec \theta \tan \theta ]_0^\alpha & - &
 +
a^2 \int_0^\alpha \sec \theta \tan^2 \theta \, d\theta & \\
 +
& = & a^2 \sec \alpha \tan \alpha & -
 +
& a^2 \int_0^\alpha \sec^3 \theta \, d\theta & +
 +
a^2 \int_0^\alpha \sec \theta \, d\theta \\
 +
& = & a^2 \sec \alpha \tan \alpha & -
 +
& I & + a^2 \int_0^\alpha \sec \theta \, d\theta \\
 +
\end{matrix}</math>
 +
 
 +
After integrating by parts, and using trigonometric identities, we've ended up with an expression involving the original integral. In cases like this we must now rearrange the equation so that the original integral is on one side only
 +
 
 +
:{|
 +
|<math>I</math>
 +
|<math>=\tfrac{a^2}{2}\Bigg(\sec(\alpha)\tan(\alpha)+\int\limits_0^\alpha \sec(\theta)d\theta\Bigg)</math>
 +
|-
 +
|
 +
|<math>=\tfrac{a^2}{2}\Bigg(\sec(\alpha)\tan(\alpha)+\bigg[\ln\Big(\sec(\theta)+\tan(\theta)\Big)\bigg]_0^\alpha\Bigg)</math>
 +
|-
 +
|
 +
|<math>=\tfrac{a^2}{2}\bigg(\sec(\alpha)\tan(\alpha)+a^2\ln\Big(\sec(\alpha)+\tan(\alpha)\Big)\bigg)</math>
 +
|-
 +
|
 +
|<math>=\tfrac{a^2}{2}\bigg(\tfrac{z}{a^2}\sqrt{a^2+z^2}+\ln\left(\tfrac{z+\sqrt{a^2+z^2}}{a}\right)\bigg)</math>
 +
|-
 +
|
 +
|<math>=\tfrac{1}{2}\bigg(z\sqrt{z^2+a^2}+a^2\ln\left(\tfrac{z+\sqrt{a^2+z^2}}{a}\right)\bigg)</math>
 +
|}
 +
 
 +
As we would expect from the integrand, this is approximately <math>\frac{z^2}{2}</math> for large <math>z</math> .
 +
 
 +
In some cases it is possible to do trigonometric substitution in cases when there is no <math>\sqrt{\ \ }</math> appearing in the integral. 
 +
 
 +
'''Example'''
 +
:<math>\int\frac{dx}{x^2+1}</math>
 +
 
 +
The denominator of this function is equal to <math>\bigl(\sqrt{1+x^2}\bigr)^2</math> . This suggests that we try to substitute <math>x=\tan(u)</math> and use the identity <math>1+\tan^2(u)=\sec^2(u)</math> . With this substitution, we obtain that <math>dx=\sec^2(u)du</math> and thus
 +
:<math>\int\frac{dx}{x^2+1}=\int\frac{\sec^2(u)}{\tan^2(u)+1}du</math>
 +
 
 +
:<math>=\int\frac{\sec^2(u)}{\sec^2(u)}du</math>
 +
:<math>=\int du</math>
 +
:<math>=u+c</math>
 +
Using the initial substitution
 +
<math>u=\arctan(x)</math>
 +
gives
 +
:<math>\int\frac{dx}{x^2+1}=\arctan(x)+C</math>
 +
 
 +
===Secant substitution===
 +
[[Image:Trig_Sub_Triangle_3.png|frame|right|273px|This substitution is easily derived from a triangle, using the [[w:Pythagorean_Theorem|Pythagorean Theorem]].]]
 +
 
 +
If the integrand contains a factor of the form  <math>\displaystyle\sqrt{x^2-a^2}</math> we use the substitution
 +
:<math>x=a\sec(\theta)\quad dx=a\sec(\theta)\tan(\theta)d\theta\quad\sqrt{x^2-a^2}=a\tan(\theta)</math>
 +
 
 +
==== Example 1 ====
 +
Find <math>\int\limits_0^z \frac{\sqrt{x^2-1}}{x}dx</math> .
 +
 
 +
:{|
 +
|<math>\int\limits_0^z \frac{\sqrt{x^2-1}}{x}dx</math>
 +
|<math>=\int\limits_0^\alpha \frac{\tan(\theta)}{\sec(\theta)}\sec(\theta)\tan(\theta)d\theta\qquad z>1</math>
 +
|-
 +
|
 +
|<math>=\int\limits_0^\alpha \tan^2(\theta)d\theta\qquad\qquad\qquad\qquad\alpha=\arcsec(z)</math>
 +
|-
 +
|
 +
|<math>=\bigg[\tan(\theta)-\theta\bigg]_0^\alpha\qquad\qquad\qquad\tan(\alpha)=\sqrt{\sec^2(\alpha)-1}</math>
 +
|-
 +
|
 +
|<math>=\tan(\alpha)-\alpha\qquad\qquad\qquad\qquad\tan(\alpha)=\sqrt{z^2-1}</math>
 +
|-
 +
|
 +
|<math>=\sqrt{z^2-1}-\arcsec(z)</math>
 +
|}
 +
 
 +
==== Example 2 ====
 +
Find <math>\int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx</math> .
 +
 
 +
:{|
 +
|<math>\int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx</math>
 +
|<math>=\int\limits_1^\alpha \frac{\tan(\theta)}{\sec^2(\theta)}\sec(\theta)\tan(\theta)d\theta\qquad z>1</math>
 +
|-
 +
|
 +
|<math>=\int\limits_0^\alpha \frac{\sin^2(\theta)}{\cos(\theta)}d\theta\qquad\qquad\qquad\alpha=\arcsec(z)</math>
 +
|}
 +
 
 +
We can now integrate by parts
 +
:{|
 +
|<math>\int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx</math>
 +
|<math>=-\bigg[\tan(\theta)\cos(\theta)\bigg]_0^\alpha+\int\limits_0^\alpha \sec(\theta)d\theta</math>
 +
|-
 +
|
 +
|<math>=-\sin(\alpha)+\bigg[\ln\bigl(\sec(\theta)+ \tan(\theta)\bigr)\bigg]_0^\alpha</math>
 +
|-
 +
|
 +
|<math>=\ln\bigl(\sec(\alpha)+\tan(\alpha)\bigr)-\sin(\alpha)</math>
 +
|-
 +
|
 +
|<math>=\ln\bigl(z+\sqrt{z^2-1}\bigr)-\frac{\sqrt{z^2-1}}{z}</math>
 +
|}
 +
 
 +
==Resources==
 +
*[https://youtu.be/BVn8x7wCa3A Ex 1: Integration Using Trigonometric Substitution] by James Sousa
 +
 
 +
*[https://youtu.be/a-f63vZVuBQ Ex 2: Integration Using Trigonometric Substitution] by James Sousa
 +
 
 +
*[https://youtu.be/jZa4FM6l6pM Ex 3: Integration Using Trigonometric Substitution] by James Sousa
 +
 
 +
*[https://youtu.be/ObxsrPx44nw Ex 4: Integration Using Trigonometric Substitution] by James Sousa
 +
 
 +
*[https://youtu.be/OnT7Ub68FWg Ex 5: Integration Using Trigonometric Substitution] by James Sousa
 +
 
 +
*[https://youtu.be/3lC5AuCFK4c Trigonometric Substitution - Example 1] by patrickJMT
 +
 
 +
*[https://youtu.be/GVL4lHX6DgM Trigonometric Substitution - Example 2] by patrickJMT
 +
 
 +
*[https://youtu.be/yW6Odu0YHL0 Trigonometric Substitution - Example 3 Part 1] by patrickJMT
 +
 
 +
*[https://youtu.be/4QNntd_KZbc Trigonometric Substitution - Example 4 Rational Powers] by patrickJMT
 +
 
 +
*[https://youtu.be/wuRNmNDLanc Trigonometric Substitution More Examples] by patrickJMT

Revision as of 00:44, 9 October 2021

The idea behind the trigonometric substitution is quite simple: to replace expressions involving square roots with expressions that involve standard trigonometric functions, but no square roots. Integrals involving trigonometric functions are often easier to solve than integrals involving square roots.

Let us demonstrate this idea in practice. Consider the expression Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{1-x^2}} . Probably the most basic trigonometric identity is for an arbitrary angle . If we replace in this expression by , with the help of this trigonometric identity we see

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{1-x^2}=\sqrt{1-\sin^2(\theta)}=\sqrt{\cos^2(\theta)}=\cos(\theta)}

Note that we could write Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\arcsin(x)} since we replaced Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2} with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin^2(\theta)} .

We would like to mention that technically one should write the absolute value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(\theta)} , in other words Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigl|\cos(\theta)\bigr|} as our final answer since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{a^2}=|a|} for all possible Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} . But as long as we are careful about the domain of all possible Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and how Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(\theta)} is used in the final computation, omitting the absolute value signs does not constitute a problem. However, we cannot directly interchange the simple expression Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(\theta)} with the complicated Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{1-x^2}} wherever it may appear, we must remember when integrating by substitution we need to take the derivative into account. That is we need to remember that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx=\cos(\theta)d\theta} , and to get a integral that only involves Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} we need to also replace Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx} by something in terms of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\theta} . Thus, if we see an integral of the form

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\sqrt{1-x^2}dx}

we can rewrite it as

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\cos(\theta)\cos(\theta)d\theta=\int\cos^2(\theta)d\theta}

Notice in the expression on the left that the first Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(\theta)} comes from replacing the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{1-x^2}} and the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(\theta)d\theta} comes from substituting for the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx} .

Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos^2(\theta)=\frac{1+\cos(2\theta)}{2}} our original integral reduces to:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac12\int d\theta+\tfrac12\int\cos(2\theta)d\theta} .

These last two integrals are easily handled. For the first integral we get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac12\int d\theta=\tfrac12\theta}

For the second integral we do a substitution, namely Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=2\theta,du=2d\theta} to get:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac12\int\cos(2\theta)d\theta=\tfrac12\int\cos(u)\tfrac12du=\tfrac14\sin(u)=\frac{\sin(2\theta)}{4}}

Finally we see that:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\cos^2(\theta)d\theta=\frac{\theta}{2}+\frac{\sin(2\theta)}{4}=\frac{\theta+\sin(\theta)\cos(\theta)}{2}}

However, this is in terms of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} and not in terms of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , so we must substitute back in order to rewrite the answer in terms of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .

That is we worked out that:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin(\theta)=x\qquad\cos(\theta)=\sqrt{1-x^2}\qquad\theta=\arcsin(x)}

So we arrive at our final answer

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\sqrt{1-x^2}dx=\frac{\arcsin(x)+x\sqrt{1-x^2}}{2}}

As you can see, even for a fairly harmless looking integral this technique can involve quite a lot of calculation. Often it is helpful to see if a simpler method will suffice before turning to trigonometric substitution. On the other hand, frequently in the case of integrands involving square roots, this is the most tractable way to solve the problem. We begin with giving some rules of thumb to help you decide which trigonometric substitutions might be helpful.

If the integrand contains a single factor of one of the forms Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{a^2-x^2}\mbox{ or }\sqrt{a^2+x^2}\mbox{ or }\sqrt{x^2-a^2}} we can try a trigonometric substitution.

  • If the integrand contains Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{a^2-x^2}} let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\sin(\theta)} and use the identity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-\sin^2(\theta)=\cos^2(\theta)} .
  • If the integrand contains Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{a^2+x^2}} let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\tan(\theta)} and use the identity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\tan^2(\theta)=\sec^2(\theta)} .
  • If the integrand contains Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{x^2-a^2}} let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\sec(\theta)} and use the identity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sec^2(\theta)-1=\tan^2(\theta)} .
Trigonometric Substitutions
Trigonometric Substitutions

Sine substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

If the integrand contains a piece of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{a^2-x^2}} we use the substitution

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\sin(\theta)\quad dx=a\cos(\theta)d\theta}

This will transform the integrand to a trigonometric function. If the new integrand can't be integrated on sight then the tan-half-angle substitution described below will generally transform it into a more tractable algebraic integrand.

E.g., if the integrand is ,

If the integrand is , we can rewrite it as

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\frac{1+x}{1-x}}=\sqrt{\frac{1+x}{1+x}\cdot\frac{1+x}{1-x}}=\frac{1+x}{\sqrt{1-x^2}}}

Then we can make the substitution

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int\limits_0^a\frac{1+x}{\sqrt{1-x^2}}dx&=\int\limits_0^\alpha\frac{1+\sin(\theta)}{\cos(\theta)}\cos(\theta)d\theta &0<a<1\\ &=\int\limits_0^\alpha\bigl(1+\sin(\theta)\bigr)d\theta&\alpha=\arcsin(a)\\ &=\alpha+\Big[-\cos(\theta)\Big]_0^\alpha\\ &=\alpha+1-\cos(\alpha)\\ &=1+\arcsin(a)-\sqrt{1-a^2} \end{align}}

Tangent substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

When the integrand contains a piece of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{a^2+x^2}} we use the substitution

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\tan(\theta)\qquad\sqrt{x^2+a^2}=a\sec(\theta)\qquad dx=a\sec^2(\theta)d\theta}

E.g., if the integrand is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x^2+a^2)^{-\frac32}} then on making this substitution we find

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int\limits_0^z(x^2+a^2)^{-\frac32}dx&=a^{-2}\int\limits_0^\alpha \cos(\theta)d\theta&z>0\\ &=a^{-2}\Big[\sin(\theta)\Big]_0^\alpha&\alpha=\arctan\left(\tfrac{z}{a}\right)\\ &=a^{-2}\sin(\alpha)\\ &=a^{-2}\frac{\frac{z}{a}}{\sqrt{1+\frac{z^2}{a^2}}}\\ &=\frac{z}{a^2\sqrt{a^2+z^2}} \end{align}}

If the integral is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I=\int\limits_0^z\sqrt{x^2+a^2}\qquad z>0}

then on making this substitution we find

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} I & = & a^2 \int_0^\alpha \sec^3 \theta \, d\theta & & & \alpha = \tan^{-1} (z/a) \\ & = & a^2 \int_0^\alpha \sec \theta \, d\tan \theta & & & \\ & = & a^2 [ \sec \theta \tan \theta ]_0^\alpha & - & a^2 \int_0^\alpha \sec \theta \tan^2 \theta \, d\theta & \\ & = & a^2 \sec \alpha \tan \alpha & - & a^2 \int_0^\alpha \sec^3 \theta \, d\theta & + a^2 \int_0^\alpha \sec \theta \, d\theta \\ & = & a^2 \sec \alpha \tan \alpha & - & I & + a^2 \int_0^\alpha \sec \theta \, d\theta \\ \end{matrix}}

After integrating by parts, and using trigonometric identities, we've ended up with an expression involving the original integral. In cases like this we must now rearrange the equation so that the original integral is on one side only

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\tfrac{a^2}{2}\Bigg(\sec(\alpha)\tan(\alpha)+\int\limits_0^\alpha \sec(\theta)d\theta\Bigg)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\tfrac{a^2}{2}\Bigg(\sec(\alpha)\tan(\alpha)+\bigg[\ln\Big(\sec(\theta)+\tan(\theta)\Big)\bigg]_0^\alpha\Bigg)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\tfrac{a^2}{2}\bigg(\sec(\alpha)\tan(\alpha)+a^2\ln\Big(\sec(\alpha)+\tan(\alpha)\Big)\bigg)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\tfrac{a^2}{2}\bigg(\tfrac{z}{a^2}\sqrt{a^2+z^2}+\ln\left(\tfrac{z+\sqrt{a^2+z^2}}{a}\right)\bigg)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\tfrac{1}{2}\bigg(z\sqrt{z^2+a^2}+a^2\ln\left(\tfrac{z+\sqrt{a^2+z^2}}{a}\right)\bigg)}

As we would expect from the integrand, this is approximately Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z^2}{2}} for large Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} .

In some cases it is possible to do trigonometric substitution in cases when there is no Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\ \ }} appearing in the integral.

Example

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\frac{dx}{x^2+1}}

The denominator of this function is equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigl(\sqrt{1+x^2}\bigr)^2} . This suggests that we try to substitute Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\tan(u)} and use the identity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\tan^2(u)=\sec^2(u)} . With this substitution, we obtain that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx=\sec^2(u)du} and thus

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\frac{dx}{x^2+1}=\int\frac{\sec^2(u)}{\tan^2(u)+1}du}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int\frac{\sec^2(u)}{\sec^2(u)}du}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int du}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =u+c}

Using the initial substitution Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=\arctan(x)} gives

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\frac{dx}{x^2+1}=\arctan(x)+C}

Secant substitution

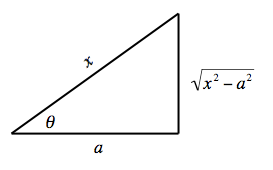
This substitution is easily derived from a triangle, using the Pythagorean Theorem.

If the integrand contains a factor of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle\sqrt{x^2-a^2}} we use the substitution

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\sec(\theta)\quad dx=a\sec(\theta)\tan(\theta)d\theta\quad\sqrt{x^2-a^2}=a\tan(\theta)}

Example 1

Find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\limits_0^z \frac{\sqrt{x^2-1}}{x}dx} .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\limits_0^z \frac{\sqrt{x^2-1}}{x}dx} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int\limits_0^\alpha \frac{\tan(\theta)}{\sec(\theta)}\sec(\theta)\tan(\theta)d\theta\qquad z>1}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int\limits_0^\alpha \tan^2(\theta)d\theta\qquad\qquad\qquad\qquad\alpha=\arcsec(z)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\bigg[\tan(\theta)-\theta\bigg]_0^\alpha\qquad\qquad\qquad\tan(\alpha)=\sqrt{\sec^2(\alpha)-1}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\tan(\alpha)-\alpha\qquad\qquad\qquad\qquad\tan(\alpha)=\sqrt{z^2-1}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{z^2-1}-\arcsec(z)}

Example 2

Find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx} .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int\limits_1^\alpha \frac{\tan(\theta)}{\sec^2(\theta)}\sec(\theta)\tan(\theta)d\theta\qquad z>1}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int\limits_0^\alpha \frac{\sin^2(\theta)}{\cos(\theta)}d\theta\qquad\qquad\qquad\alpha=\arcsec(z)}

We can now integrate by parts

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\limits_1^z \frac{\sqrt{x^2-1}}{x^2}dx} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\bigg[\tan(\theta)\cos(\theta)\bigg]_0^\alpha+\int\limits_0^\alpha \sec(\theta)d\theta}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\sin(\alpha)+\bigg[\ln\bigl(\sec(\theta)+ \tan(\theta)\bigr)\bigg]_0^\alpha}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\ln\bigl(\sec(\alpha)+\tan(\alpha)\bigr)-\sin(\alpha)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\ln\bigl(z+\sqrt{z^2-1}\bigr)-\frac{\sqrt{z^2-1}}{z}}

Resources

Retrieved from "https://mathresearch.utsa.edu/wiki/index.php?title=Trigonometric_Substitution&oldid=2018"