Difference between revisions of "Absolute Value Functions"
Jump to navigation
Jump to search
(Created page with "In mathematics, the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x if x is positive, and...") |
|||
| Line 1: | Line 1: | ||
In mathematics, the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x if x is positive, and |x| = −x if x is negative (in which case −x is positive), and |0| = 0. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its "distance from zero". | In mathematics, the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x if x is positive, and |x| = −x if x is negative (in which case −x is positive), and |0| = 0. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its "distance from zero". | ||
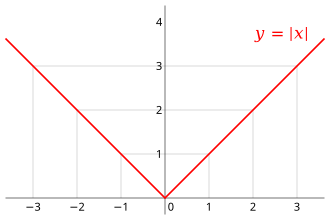
| + | [[Image:Absolute value.svg|thumb|The [[graph of a function|graph]] of the absolute value function for real numbers]] | ||
Revision as of 11:44, 15 September 2021
In mathematics, the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x if x is positive, and |x| = −x if x is negative (in which case −x is positive), and |0| = 0. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its "distance from zero".

The graph of the absolute value function for real numbers