Difference between revisions of "The Cross Product"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
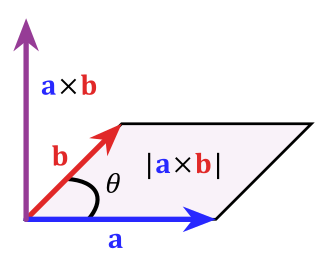
[[File:Cross product parallelogram.svg|thumb|Cross_product_parallelogram]] | [[File:Cross product parallelogram.svg|thumb|Cross_product_parallelogram]] | ||
The cross product is an operation between two 3-dimensional vectors that returns a third vector orthogonal (i.e., perpendicular) to the first two. For vectors <math> \mathbf{u} = \langle u_1, u_2, u_3 \rangle </math> and <math> \mathbf{v} = \langle v_1, v_2, v_3 \rangle </math>, the cross product of <math> \mathbf{u} </math> and <math> \mathbf{v} </math> (notated as <math> u \times v </math>) is <math> \mathbf{w} = \langle u_2v_3 - u_3v_2, -(u_1v_3 - u_3v_1), u_1v_2 - u_2v_1 \rangle</math>. | The cross product is an operation between two 3-dimensional vectors that returns a third vector orthogonal (i.e., perpendicular) to the first two. For vectors <math> \mathbf{u} = \langle u_1, u_2, u_3 \rangle </math> and <math> \mathbf{v} = \langle v_1, v_2, v_3 \rangle </math>, the cross product of <math> \mathbf{u} </math> and <math> \mathbf{v} </math> (notated as <math> u \times v </math>) is <math> \mathbf{w} = \langle u_2v_3 - u_3v_2, -(u_1v_3 - u_3v_1), u_1v_2 - u_2v_1 \rangle</math>. | ||
| + | The cross product of <math> \mathbf{u} </math> and <math> \mathbf{v} </math> can also be written in determinant form like so: | ||
| − | <math>\begin{vmatrix} | + | <math>\mathbf{w} = det\begin{vmatrix} |
i & j & k\\ | i & j & k\\ | ||
u_1 & u_2 & u_3\\ | u_1 & u_2 & u_3\\ | ||
Revision as of 17:25, 20 September 2021
The cross product is an operation between two 3-dimensional vectors that returns a third vector orthogonal (i.e., perpendicular) to the first two. For vectors and , the cross product of and (notated as ) is . The cross product of and can also be written in determinant form like so:
Resources
- The Cross Product, OpenStax
- Cross Product, Cornell University
