Difference between revisions of "The Cross Product"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
<math>\mathbf{w} = \textrm{det}\begin{vmatrix} | <math>\mathbf{w} = \textrm{det}\begin{vmatrix} | ||
| − | i & j & k\\ | + | \mathbf{i} & \mathbf{j} & \mathbf{k}\\ |
u_1 & u_2 & u_3\\ | u_1 & u_2 & u_3\\ | ||
v_1 & v_2 & v_3\\ | v_1 & v_2 & v_3\\ | ||
\end{vmatrix} = | \end{vmatrix} = | ||
| − | (u_2v_3 - u_3v_2) - (u_1v_3 - u_3v_1) + (u_1v_2 - u_2v_1) | + | (u_2v_3 - u_3v_2)\mathbf{i} - (u_1v_3 - u_3v_1)\mathbf{j} + (u_1v_2 - u_2v_1)\mathbf{k} |
</math> | </math> | ||
Revision as of 17:30, 20 September 2021
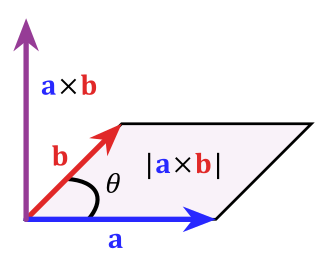
The cross product is an operation between two 3-dimensional vectors that returns a third vector orthogonal (i.e., perpendicular) to the first two. For vectors and , the cross product of and (notated as ) is . One way to remember the cross product of and is to calculate it with the following determinant:
Resources
- The Cross Product, OpenStax
- Cross Product, Cornell University