The Geometric Interpretation of the Determinant

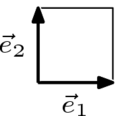
This parallelogram picture

is familiar from the construction of the sum of the two vectors. One way to compute the area that it encloses is to draw this rectangle and subtract the area of each subregion.

         ${\begin{array}{l}{\text{area of parallelogram}}\\\quad ={\text{area of rectangle}}-{\text{area of }}A-{\text{area of }}B\\\qquad -\cdots -{\text{area of }}F\\\quad =(x_{1}+x_{2})(y_{1}+y_{2})-x_{2}y_{1}-x_{1}y_{1}/2\\\qquad -x_{2}y_{2}/2-x_{2}y_{2}/2-x_{1}y_{1}/2-x_{2}y_{1}\\\quad =x_{1}y_{2}-x_{2}y_{1}\end{array}}$

The fact that the area equals the value of the determinant

${\begin{vmatrix}x_{1}&x_{2}\\y_{1}&y_{2}\end{vmatrix}}=x_{1}y_{2}-x_{2}y_{1}$

is no coincidence.

The properties in the definition of determinants make reasonable postulates for a function that measures the size of the region enclosed by the vectors in the matrix.

For instance, this shows the effect of multiplying one of the box-defining vectors by a scalar (the scalar used is $k=1.4$).

        

The region formed by $k{\vec {v}}$ and ${\vec {w}}$ is bigger, by a factor of $k$, than the shaded region enclosed by ${\vec {v}}$ and ${\vec {w}}$. That is, ${\text{size}}\,(k{\vec {v}},{\vec {w}})=k\cdot {\text{size}}\,({\vec {v}},{\vec {w}})$ and in general we expect of the size measure that ${\text{size}}\,(\dots ,k{\vec {v}},\dots )=k\cdot {\text{size}}\,(\dots ,{\vec {v}},\dots )$. Of course, this postulate is already familiar as one of the properties in the defintion of determinants.

Another property of determinants is that they are unaffected by pivoting. Here are before-pivoting and after-pivoting boxes (the scalar used is $k=0.35$).

    

Although the region on the right, the box formed by $v$ and $k{\vec {v}}+{\vec {w}}$, is more slanted than the shaded region, the two have the same base and the same height and hence the same area. This illustrates that ${\text{size}}\,({\vec {v}},k{\vec {v}}+{\vec {w}})={\text{size}}\,({\vec {v}},{\vec {w}})$. Generalized, ${\text{size}}\,(\dots ,{\vec {v}},\dots ,{\vec {w}},\dots )={\text{size}}\,(\dots ,{\vec {v}},\dots ,k{\vec {v}}+{\vec {w}},\dots )$, which is a restatement of the determinant postulate.

Of course, this picture

shows that ${\text{size}}\,({\vec {e}}_{1},{\vec {e}}_{2})=1$, and we naturally extend that to any number of dimensions ${\text{size}}\,({\vec {e}}_{1},\dots ,{\vec {e}}_{n})=1$, which is a restatement of the property that the determinant of the identity matrix is one.

With that, because property (2) of determinants is redundant (as remarked right after the definition), we have that all of the properties of determinants are reasonable to expect of a function that gives the size of boxes. We can now cite the work done in the prior section to show that the determinant exists and is unique to be assured that these postulates are consistent and sufficient (we do not need any more postulates). That is, we've got an intuitive justification to interpret $\det({\vec {v}}_{1},\dots ,{\vec {v}}_{n})$ as the size of the box formed by the vectors.

Example 1.1: The volume of this parallelepiped, which can be found by the usual formula from high school geometry, is $12$.

         ${\begin{vmatrix}2&0&-1\\0&3&0\\2&1&1\end{vmatrix}}=12$

Remark 1.2: Although property (2) of the definition of determinants is redundant, it raises an important point. Consider these two.

${\begin{vmatrix}4&1\\2&3\end{vmatrix}}=10$	${\begin{vmatrix}1&4\\3&2\end{vmatrix}}=-10$

The only difference between them is in the order in which the vectors are taken. If we take ${\vec {u}}$ first and then go to ${\vec {v}}$, follow the counterclockwise arc shown, then the sign is positive. Following a clockwise arc gives a negative sign.

The sign returned by the size function reflects the "orientation" or "sense" of the box. (We see the same thing if we picture the effect of scalar multiplication by a negative scalar.)

Although it is both interesting and important, the idea of orientation turns out to be tricky. It is not needed for the development below, and so we will pass it by.

Definition 1.3: The box (or parallelepiped) formed by $\langle {\vec {v}}_{1},\dots ,{\vec {v}}_{n}\rangle$ (where each vector is from $\mathbb {R} ^{n}$) includes all of the set $\{t_{1}{\vec {v}}_{1}+\dots +t_{n}{\vec {v}}_{n}\,{\big |}\,t_{1},\ldots ,t_{n}\in [0..1]\}$. The volume of a box is the absolute value of the determinant of the matrix with those vectors as columns.

Example 1.4: Volume, because it is an absolute value, does not depend on the order in which the vectors are given. The volume of the parallelepiped in can also be computed as the absolute value of this determinant.

${\begin{vmatrix}0&2&-1\\3&0&0\\1&2&1\end{vmatrix}}=-12$

The definition of volume gives a geometric interpretation to something in the space, boxes made from vectors. The next result relates the geometry to the functions that operate on spaces.

Theorem 1.5: A transformation $t:\mathbb {R} ^{n}\to \mathbb {R} ^{n}$ changes the size of all boxes by the same factor, namely the size of the image of a box $\left|t(S)\right|$ is $\left|T\right|$ times the size of the box $\left|S\right|$, where $T$ is the matrix representing $t$ with respect to the standard basis. That is, for all $n\!\times \!n$ matrices, the determinant of a product is the product of the determinants $\left|TS\right|=\left|T\right|\cdot \left|S\right|$.

The two sentences state the same idea, first in map terms and then in matrix terms. Although we tend to prefer a map point of view, the second sentence, the matrix version, is more convienent for the proof and is also the way that we shall use this result later.

Proof: The two statements are equivalent because $\left|t(S)\right|=\left|TS\right|$, as both give the size of the box that is the image of the unit box ${\mathcal {E}}_{n}$ under the composition $t\circ s$ (where $s$ is the map represented by $S$ with respect to the standard basis).

First consider the case that $\left|T\right|=0$. A matrix has a zero determinant if and only if it is not invertible. Observe that if $TS$ is invertible, so that there is an $M$ such that $(TS)M=I$, then the associative property of matrix multiplication $T(SM)=I$ shows that $T$ is also invertible (with inverse $SM$). Therefore, if $T$ is not invertible then neither is $TS$ — if $\left|T\right|=0$ then $\left|TS\right|=0$, and the result holds in this case.

Now consider the case that $\left|T\right|\neq 0$, that $T$ is nonsingular. Recall that any nonsingular matrix can be factored into a product of elementary matrices, so that $TS=E_{1}E_{2}\cdots E_{r}S$. In the rest of this argument, we will verify that if $E$ is an elementary matrix then $\left|ES\right|=\left|E\right|\cdot \left|S\right|$. The result will follow because then $\left|TS\right|=\left|E_{1}\cdots E_{r}S\right|=\left|E_{1}\right|\cdots \left|E_{r}\right|\cdot \left|S\right|=\left|E_{1}\cdots E_{r}\right|\cdot \left|S\right|=\left|T\right|\cdot \left|S\right|$.

If the elementary matrix $E$ is $M_{i}(k)$ then $M_{i}(k)S$ equals $S$ except that row $i$ has been multiplied by $k$. The third property of determinant functions then gives that $\left|M_{i}(k)S\right|=k\cdot \left|S\right|$. But $\left|M_{i}(k)\right|=k$, again by the third property because $M_{i}(k)$ is derived from the identity by multiplication of row $i$ by $k$, and so $\left|ES\right|=\left|E\right|\cdot \left|S\right|$ holds for $E=M_{i}(k)$. The $E=P_{i,j}=-1$ and $E=C_{i,j}(k)$ checks are similar.

Example 1.6: Application of the map $t$ represented with respect to the standard bases by

${\begin{pmatrix}1&1\\-2&0\end{pmatrix}}$

will double sizes of boxes, e.g., from this

         ${\begin{vmatrix}2&1\\1&2\end{vmatrix}}=3$

to this

         ${\begin{vmatrix}3&3\\-4&-2\end{vmatrix}}=6$

Corollary 1.7: If a matrix is invertible then the determinant of its inverse is the inverse of its determinant $\left|T^{-1}\right|=1/\left|T\right|$.

Proof: $1=\left|I\right|=\left|TT^{-1}\right|=\left|T\right|\cdot \left|T^{-1}\right|$

Recall that determinants are not additive homomorphisms, $\det(A+B)$ need not equal $\det(A)+\det(B)$. The above theorem says, in contrast, that determinants are multiplicative homomorphisms: $\det(AB)$ does equal $\det(A)\cdot \det(B)$.

Licensing

Content obtained and/or adapted from:

• Determinants as Size Functions, Wikibooks: Linear Algebra under a CC BY-SA license