Difference between revisions of "Functions:Surjective"
| Line 1: | Line 1: | ||
| − | + | {{short description|Function such that every element has a preimage (mathematics)}} | |
| + | {{Redirect|Onto|3=wiktionary:onto}} | ||
| + | {{Functions}} | ||
| + | In [[mathematics]], a '''surjective function''' (also known as '''surjection''', or '''onto function''') is a [[Function (mathematics)|function]] {{math|''f''}} that maps an element {{math|''x''}} to every element {{math|''y''}}; that is, for every {{math|''y''}}, there is an {{math|''x''}} such that {{math|''f''(''x'') {{=}} ''y''}}. In other words, every element of the function's [[codomain]] is the [[Image (mathematics)|image]] of {{em|at least}} one element of its [[Domain of a function|domain]].<ref name=":0">{{Cite web|url=https://www.mathsisfun.com/sets/injective-surjective-bijective.html|title=Injective, Surjective and Bijective|website=www.mathsisfun.com|access-date=2019-12-07}}</ref><ref name=":1">{{Cite web|url=https://brilliant.org/wiki/bijection-injection-and-surjection/|title=Bijection, Injection, And Surjection {{!}} Brilliant Math & Science Wiki|website=brilliant.org|language=en-us|access-date=2019-12-07}}</ref> It is not required that {{math|''x''}} be [[unique (mathematics)|unique]]; the function {{math|''f''}} may map one or more elements of {{math|''X''}} to the same element of {{math|''Y''}}. | ||
| − | + | {{Gallery | |
| − | + | |lines=4 | |
| + | |align=center | ||
| + | |Image:Surjection.svg|A non-injective '''surjective''' function (surjection, not a bijection) | ||
| + | |Image:Bijection.svg|An injective '''surjective''' function (bijection) | ||
| + | |Image:Injection.svg|An injective non-surjective function (injection, not a bijection) | ||
| + | |Image:Not-Injection-Surjection.svg|A non-injective non-surjective function (also not a bijection) | ||
| + | }} | ||
| − | + | The term ''surjective'' and the related terms ''[[injective function|injective]]'' and ''[[bijective function|bijective]]'' were introduced by [[Nicolas Bourbaki]],<ref>{{Citation | url = http://jeff560.tripod.com/i.html | title = Earliest Uses of Some of the Words of Mathematics | contribution = Injection, Surjection and Bijection | publisher = Tripod |first=Jeff|last=Miller}}.</ref><ref>{{Cite book|url=https://books.google.com/books?id=-CXn6y_1nJ8C&q=injection+surjection+bijection+bourbaki&pg=PA106|title=Bourbaki|last=Mashaal|first=Maurice|date=2006|publisher=American Mathematical Soc.|isbn=978-0-8218-3967-6|pages=106|language=en}}</ref> a group of mainly [[France|French]] 20th-century [[mathematician]]s who, under this pseudonym, wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. The French word ''[[wikt:sur#French|sur]]'' means ''over'' or ''above'', and relates to the fact that the [[image (mathematics)|image]] of the domain of a surjective function completely covers the function's codomain. | |
| − | + | Any function induces a surjection by [[restriction of a function|restricting]] its codomain to the image of its domain. Every surjective function has a [[Inverse function#Left and right inverses|right inverse]], and every function with a right inverse is necessarily a surjection. The [[function composition|composition]] of surjective functions is always surjective. Any function can be decomposed into a surjection and an injection. | |
| − | + | ==Definition== | |
| + | {{details|topic=notation|Function (mathematics)#Notation}} | ||
| + | A '''surjective function''' is a [[function(mathematics)|function]] whose [[image (mathematics)|image]] is equal to its [[codomain]]. Equivalently, a function <math>f</math> with [[domain of a function|domain]] <math>X</math> and codomain <math>Y</math> is surjective if for every <math>y</math> in <math>Y</math> there exists at least one <math>x</math> in <math>X</math> with <math>f(x)=y</math>.<ref name=":0" /> Surjections are sometimes denoted by a two-headed rightwards arrow ({{unichar|21A0|RIGHTWARDS TWO HEADED ARROW|ulink=Unicode}}),<ref name="Unicode Arrows">{{cite web| title = Arrows – Unicode| url = https://www.unicode.org/charts/PDF/U2190.pdf| access-date = 2013-05-11}}</ref> as in <math>f\colon X\twoheadrightarrow Y</math>. | ||
| + | |||
| + | Symbolically, | ||
| + | |||
| + | :If <math>f\colon X \rightarrow Y</math>, then <math>f</math> is said to be surjective if | ||
| + | |||
| + | :<math>\forall y \in Y, \, \exists x \in X, \;\; f(x)=y</math>.<ref name=":1" /><ref>{{Cite web|url=http://www.math.umaine.edu/~farlow/sec42.pdf|title=Injections, Surjections, and Bijections|last=Farlow|first=S. J.|author-link= Stanley Farlow |website=math.umaine.edu|access-date=2019-12-06}}</ref> | ||
| + | |||
| + | ==Examples== | ||
| + | [[File:Codomain2.SVG|right|thumb|250px|'''A non-surjective function''' from [[domain of a function|domain]] ''X'' to [[codomain]] ''Y''. The smaller yellow oval inside ''Y'' is the [[Image (mathematics)|image]] (also called [[range of a function|range]]) of ''f''. This function is '''not''' surjective, because the image does not fill the whole codomain. In other words, ''Y'' is colored in a two-step process: First, for every ''x'' in ''X'', the point ''f''(''x'') is colored yellow; Second, all the rest of the points in ''Y'', that are not yellow, are colored blue. The function ''f'' would be surjective only if there were no blue points.]] | ||
| + | |||
| + | * For any set ''X'', the [[identity function]] id<sub>''X''</sub> on ''X'' is surjective. | ||
| + | * The function {{math|''f'' : '''Z''' → {0, 1}<nowiki/>}} defined by ''f''(''n'') = ''n'' '''[[Modular arithmetic|mod]]''' 2 (that is, [[even number|even]] [[integer]]s are mapped to 0 and [[odd number|odd]] integers to 1) is surjective. | ||
| + | * The function {{math|''f'' : '''R''' → '''R'''}} defined by ''f''(''x'') = 2''x'' + 1 is surjective (and even [[bijective function|bijective]]), because for every [[real number]] ''y'', we have an ''x'' such that ''f''(''x'') = ''y'': such an appropriate ''x'' is (''y'' − 1)/2. | ||
| + | * The function {{math|''f'' : '''R''' → '''R'''}} defined by ''f''(''x'') = ''x''<sup>3</sup> − 3''x'' is surjective, because the pre-image of any [[real number]] ''y'' is the solution set of the cubic polynomial equation ''x''<sup>3</sup> − 3''x'' − ''y'' = 0, and every cubic polynomial with real coefficients has at least one real root. However, this function is not [[injective function|injective]] (and hence not [[bijective function|bijective]]), since, for example, the pre-image of ''y'' = 2 is {''x'' = −1, ''x'' = 2}. (In fact, the pre-image of this function for every ''y'', −2 ≤ ''y'' ≤ 2 has more than one element.) | ||
| + | * The function {{math|''g'' : '''R''' → '''R'''}} defined by {{Nowrap begin}}''g''(''x'') = ''x''<sup>2</sup>{{Nowrap end}} is ''not'' surjective, since there is no real number ''x'' such that {{Nowrap begin}}''x''<sup>2</sup> = −1{{Nowrap end}}. However, the function {{math|''g'' : '''R''' → '''R'''{{sub|≥0}}}} defined by {{math|1=''g''(''x'') = ''x''<sup>2</sup>}} (with the restricted codomain) ''is'' surjective, since for every ''y'' in the nonnegative real codomain ''Y'', there is at least one ''x'' in the real domain ''X'' such that {{Nowrap begin}}''x''<sup>2</sup> = ''y''{{Nowrap end}}. | ||
| + | * The [[natural logarithm]] function {{math|ln : <nowiki>(0, +∞)</nowiki> → '''R'''}} is a surjective and even bijective (mapping from the set of positive real numbers to the set of all real numbers). Its inverse, the [[exponential function]], if defined with the set of real numbers as the domain, is not surjective (as its range is the set of positive real numbers). | ||
| + | * The [[matrix exponential]] is not surjective when seen as a map from the space of all ''n''×''n'' [[matrix (mathematics)|matrices]] to itself. It is, however, usually defined as a map from the space of all ''n''×''n'' matrices to the [[general linear group]] of degree ''n'' (that is, the [[group (mathematics)|group]] of all ''n''×''n'' [[invertible matrix|invertible matrices]]). Under this definition, the matrix exponential is surjective for complex matrices, although still not surjective for real matrices. | ||
| + | * The [[projection (set theory)|projection]] from a [[cartesian product]] {{math|''A'' × ''B''}} to one of its factors is surjective, unless the other factor is empty. | ||
| + | * In a 3D video game, vectors are projected onto a 2D flat screen by means of a surjective function. | ||
| + | |||
| + | [[File:Surjective function.svg|500px|thumb|left|Interpretation for '''surjective functions''' in the Cartesian plane, defined by the mapping ''f'' : ''X'' → ''Y'', where ''y'' = ''f''(''x''), ''X'' = domain of function, ''Y'' = range of function. Every element in the range is mapped onto from an element in the domain, by the rule ''f''. There may be a number of domain elements which map to the same range element. That is, every ''y'' in ''Y'' is mapped from an element ''x'' in ''X'', more than one ''x'' can map to the same ''y''. '''Left:''' Only one domain is shown which makes ''f'' surjective. '''Right:''' two possible domains ''X''<sub>1</sub> and ''X''<sub>2</sub> are shown.]] | ||
| + | |||
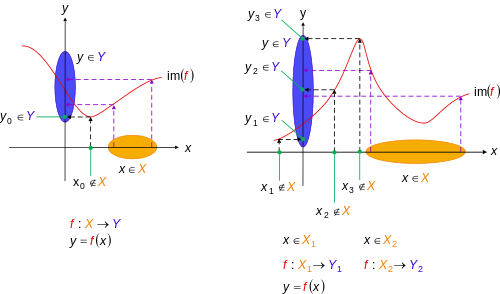
| + | [[File:Non-surjective function2.svg|500px|thumb|right|'''Non-surjective functions''' in the Cartesian plane. Although some parts of the function are surjective, where elements ''y'' in ''Y'' do have a value ''x'' in ''X'' such that ''y'' = ''f''(''x''), some parts are not. '''Left:''' There is ''y''<sub>0</sub> in ''Y'', but there is no ''x''<sub>0</sub> in ''X'' such that ''y''<sub>0</sub> = ''f''(''x''<sub>0</sub>). '''Right:''' There are ''y''<sub>1</sub>, ''y''<sub>2</sub> and ''y''<sub>3</sub> in ''Y'', but there are no ''x''<sub>1</sub>, ''x''<sub>2</sub>, and ''x''<sub>3</sub> in ''X'' such that ''y''<sub>1</sub> = ''f''(''x''<sub>1</sub>), ''y''<sub>2</sub> = ''f''(''x''<sub>2</sub>), and ''y''<sub>3</sub> = ''f''(''x''<sub>3</sub>).]] | ||
| + | |||
| + | {{-}} | ||
| + | |||
| + | ==Properties== | ||
| + | A function is [[bijective function|bijective]] if and only if it is both surjective and [[injective function|injective]]. | ||
| + | |||
| + | If (as is often done) a function is identified with its [[graph of a function|graph]], then surjectivity is not a property of the function itself, but rather a property of the [[Map (mathematics)|mapping]].<ref>{{cite book|author=T. M. Apostol|title=Mathematical Analysis|year=1981|publisher=Addison-Wesley|page=35}}</ref> This is, the function together with its codomain. Unlike injectivity, surjectivity cannot be read off of the graph of the function alone. | ||
| + | |||
| + | ===Surjections as right invertible functions=== | ||
| + | The function {{Nowrap|''g'' : ''Y'' → ''X''}} is said to be a [[Inverse function#Left and right inverses|right inverse]] of the function {{Nowrap|''f'' : ''X'' → ''Y''}} if {{Nowrap begin}}''f''(''g''(''y'')) = ''y''{{Nowrap end}} for every ''y'' in ''Y'' (''g'' can be undone by ''f''). In other words, ''g'' is a right inverse of ''f'' if the [[function composition|composition]] {{Nowrap|''f'' <small>o</small> ''g''}} of ''g'' and ''f'' in that order is the [[identity function]] on the domain ''Y'' of ''g''. The function ''g'' need not be a complete [[inverse function|inverse]] of ''f'' because the composition in the other order, {{Nowrap|''g'' <small>o</small> ''f''}}, may not be the identity function on the domain ''X'' of ''f''. In other words, ''f'' can undo or "''reverse''" ''g'', but cannot necessarily be reversed by it. | ||
| + | |||
| + | Every function with a right inverse is necessarily a surjection. The proposition that every surjective function has a right inverse is equivalent to the [[axiom of choice]]. | ||
| + | |||
| + | If {{Nowrap|''f'' : ''X'' → ''Y''}} is surjective and ''B'' is a [[subset]] of ''Y'', then {{Nowrap begin}}''f''(''f''<sup> −1</sup>(''B'')) = ''B''{{Nowrap end}}. Thus, ''B'' can be recovered from its [[preimage]] {{Nowrap|''f''<sup> −1</sup>(''B'')}}. | ||
| + | |||
| + | For example, in the first illustration above, there is some function ''g'' such that ''g''(''C'') = 4. There is also some function ''f'' such that ''f''(4) = ''C''. It doesn't matter that ''g''(''C'') can also equal 3; it only matters that ''f'' "reverses" ''g''. | ||
| + | |||
| + | <gallery> | ||
| + | File:Surjective composition.svg|Surjective composition: the first function need not be surjective. | ||
| + | File:Bijection.svg|Another surjective function. (This one happens to be a [[Bijective function|bijection]]) | ||
| + | File:Injection.svg|A '''non'''-surjective function. (This one happens to be an [[Injective function|injection]]) | ||
| + | </gallery> | ||
| + | |||
| + | ===Surjections as epimorphisms=== | ||
| + | A function {{Nowrap|''f'' : ''X'' → ''Y''}} is surjective if and only if it is [[right-cancellative]]:<ref>{{Cite book | ||
| + | |first=Robert | ||
| + | |last=Goldblatt | ||
| + | |title=Topoi, the Categorial Analysis of Logic | ||
| + | |url=http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=Gold010&id=3|access-date=2009-11-25 | ||
| + | |edition=Revised | ||
| + | |year=2006 | ||
| + | |orig-year=1984 | ||
| + | |publisher=[[Dover Publications]] | ||
| + | |isbn=978-0-486-45026-1}}</ref> given any functions {{Nowrap|''g'',''h'' : ''Y'' → ''Z''}}, whenever {{Nowrap begin}}''g'' <small>o</small> ''f'' = ''h'' <small>o</small> ''f''{{Nowrap end}}, then {{Nowrap begin}}''g'' = ''h''{{Nowrap end}}. This property is formulated in terms of functions and their [[function composition|composition]] and can be generalized to the more general notion of the [[morphism]]s of a [[category (mathematics)|category]] and their composition. Right-cancellative morphisms are called [[epimorphism]]s. Specifically, surjective functions are precisely the epimorphisms in the [[category of sets]]. The prefix ''epi'' is derived from the Greek preposition ''ἐπί'' meaning ''over'', ''above'', ''on''. | ||
| + | |||
| + | Any morphism with a right inverse is an epimorphism, but the converse is not true in general. A right inverse ''g'' of a morphism ''f'' is called a [[section (category theory)|section]] of ''f''. A morphism with a right inverse is called a [[split epimorphism]]. | ||
| + | |||
| + | ===Surjections as binary relations=== | ||
| + | Any function with domain ''X'' and codomain ''Y'' can be seen as a [[left-total relation|left-total]] and [[right-unique relation|right-unique]] binary relation between ''X'' and ''Y'' by identifying it with its [[function graph]]. A surjective function with domain ''X'' and codomain ''Y'' is then a binary relation between ''X'' and ''Y'' that is right-unique and both left-total and [[right-total relation|right-total]]. | ||
| + | |||
| + | ===Cardinality of the domain of a surjection=== | ||
| + | The [[cardinality]] of the domain of a surjective function is greater than or equal to the cardinality of its codomain: If {{Nowrap|''f'' : ''X'' → ''Y''}} is a surjective function, then ''X'' has at least as many elements as ''Y'', in the sense of [[cardinal number]]s. (The proof appeals to the [[axiom of choice]] to show that a function | ||
| + | {{Nowrap|''g'' : ''Y'' → ''X''}} satisfying ''f''(''g''(''y'')) = ''y'' for all ''y'' in ''Y'' exists. ''g'' is easily seen to be injective, thus the [[Cardinal number#Formal definition|formal definition]] of |''Y''| ≤ |''X''| is satisfied.) | ||
| + | |||
| + | Specifically, if both ''X'' and ''Y'' are [[finite set|finite]] with the same number of elements, then {{Nowrap|''f'' : ''X'' → ''Y''}} is surjective if and only if ''f'' is [[injective]]. | ||
| + | |||
| + | Given two sets ''X'' and ''Y'', the notation {{nowrap|''X'' ≤<sup>*</sup> ''Y''}} is used to say that either ''X'' is empty or that there is a surjection from ''Y'' onto ''X''. Using the axiom of choice one can show that {{nowrap|''X'' ≤<sup>*</sup> ''Y''}} and {{nowrap|''Y'' ≤<sup>*</sup> ''X''}} together imply that {{nowrap begin}}|''Y''| = |''X''|,{{nowrap end}} a variant of the [[Schröder–Bernstein theorem]]. | ||
| + | |||
| + | ===Composition and decomposition=== | ||
| + | The [[function composition|composition]] of surjective functions is always surjective: If ''f'' and ''g'' are both surjective, and the codomain of ''g'' is equal to the domain of ''f'', then {{Nowrap|''f'' <small>o</small> ''g''}} is surjective. Conversely, if {{Nowrap|''f'' <small>o</small> ''g''}} is surjective, then ''f'' is surjective (but ''g'', the function applied first, need not be). These properties generalize from surjections in the [[category of sets]] to any [[epimorphism]]s in any [[category (mathematics)|category]]. | ||
| + | |||
| + | Any function can be decomposed into a surjection and an [[injective function|injection]]: For any function {{Nowrap|''h'' : ''X'' → ''Z''}} there exist a surjection {{Nowrap|''f'' : ''X'' → ''Y''}} and an injection {{Nowrap|''g'' : ''Y'' → ''Z''}} such that {{Nowrap begin}}''h'' = ''g'' <small>o</small> ''f''{{Nowrap end}}. To see this, define ''Y'' to be the set of [[preimage]]s {{Nowrap|''h''<sup>−1</sup>(''z'')}} where ''z'' is in {{Nowrap|''h''(''X'')}}. These preimages are [[disjoint sets|disjoint]] and [[partition of a set|partition]] ''X''. Then ''f'' carries each ''x'' to the element of ''Y'' which contains it, and ''g'' carries each element of ''Y'' to the point in ''Z'' to which ''h'' sends its points. Then ''f'' is surjective since it is a projection map, and ''g'' is injective by definition. | ||
| + | |||
| + | ===Induced surjection and induced bijection=== | ||
| + | Any function induces a surjection by restricting its codomain to its range. Any surjective function induces a bijection defined on a [[quotient set|quotient]] of its domain by collapsing all arguments mapping to a given fixed image. More precisely, every surjection {{Nowrap|''f'' : ''A'' → ''B''}} can be factored as a projection followed by a bijection as follows. Let ''A''/~ be the [[equivalence class]]es of ''A'' under the following [[equivalence relation]]: ''x'' ~ ''y'' if and only if ''f''(''x'') = ''f''(''y''). Equivalently, ''A''/~ is the set of all preimages under ''f''. Let ''P''(~) : ''A'' → ''A''/~ be the [[projection map]] which sends each ''x'' in ''A'' to its equivalence class [''x'']<sub>~</sub>, and let ''f''<sub>''P''</sub> : ''A''/~ → ''B'' be the well-defined function given by ''f''<sub>''P''</sub>([''x'']<sub>~</sub>) = ''f''(''x''). Then ''f'' = ''f''<sub>''P''</sub> o ''P''(~). | ||
| + | |||
| + | == Space of surjections == | ||
| + | Given fixed {{Mvar|A}} and {{Mvar|B}}, one can form the set of surjections {{Math|''A'' ↠ ''B''}}. The [[cardinality]] of this set is one of the twelve aspects of Rota's [[Twelvefold way]], and is given by <math display="inline">|B|!\begin{Bmatrix}|A|\\|B|\end{Bmatrix}</math>, where <math display="inline">\begin{Bmatrix}|A|\\|B|\end{Bmatrix}</math> denotes a [[Stirling numbers of the second kind|Stirling number of the second kind]]. | ||
==Resources== | ==Resources== | ||
* [https://link-springer-com.libweb.lib.utsa.edu/content/pdf/10.1007%2F978-1-4419-7127-2.pdf Course Textbook], pages 154-164 | * [https://link-springer-com.libweb.lib.utsa.edu/content/pdf/10.1007%2F978-1-4419-7127-2.pdf Course Textbook], pages 154-164 | ||
| + | |||
| + | == Licensing == | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikipedia.org/wiki/Surjective_function, Surjective function, Wikipedia] under a CC BY-SA license | ||
Revision as of 16:31, 7 November 2021
[[Category:Template:Pagetype with short description]]Expression error: Unexpected < operator.
Template:Redirect Template:Functions In mathematics, a surjective function (also known as surjection, or onto function) is a function f that maps an element x to every element y; that is, for every y, there is an x such that f(x) Template:= y. In other words, every element of the function's codomain is the image of Template:Em one element of its domain.[1][2] It is not required that x be unique; the function f may map one or more elements of X to the same element of Y.
The term surjective and the related terms injective and bijective were introduced by Nicolas Bourbaki,[3][4] a group of mainly French 20th-century mathematicians who, under this pseudonym, wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. The French word sur means over or above, and relates to the fact that the image of the domain of a surjective function completely covers the function's codomain.
Any function induces a surjection by restricting its codomain to the image of its domain. Every surjective function has a right inverse, and every function with a right inverse is necessarily a surjection. The composition of surjective functions is always surjective. Any function can be decomposed into a surjection and an injection.
Definition
Template:Details A surjective function is a function whose image is equal to its codomain. Equivalently, a function with domain and codomain is surjective if for every in there exists at least one in with .[1] Surjections are sometimes denoted by a two-headed rightwards arrow (Template:Unichar),[5] as in .
Symbolically,
- If , then is said to be surjective if
Examples

- For any set X, the identity function idX on X is surjective.
- The function f : Z → {0, 1} defined by f(n) = n mod 2 (that is, even integers are mapped to 0 and odd integers to 1) is surjective.
- The function f : R → R defined by f(x) = 2x + 1 is surjective (and even bijective), because for every real number y, we have an x such that f(x) = y: such an appropriate x is (y − 1)/2.
- The function f : R → R defined by f(x) = x3 − 3x is surjective, because the pre-image of any real number y is the solution set of the cubic polynomial equation x3 − 3x − y = 0, and every cubic polynomial with real coefficients has at least one real root. However, this function is not injective (and hence not bijective), since, for example, the pre-image of y = 2 is {x = −1, x = 2}. (In fact, the pre-image of this function for every y, −2 ≤ y ≤ 2 has more than one element.)
- The function g : R → R defined by Template:Nowrap beging(x) = x2Template:Nowrap end is not surjective, since there is no real number x such that Template:Nowrap beginx2 = −1Template:Nowrap end. However, the function g : R → RTemplate:Sub defined by g(x) = x2 (with the restricted codomain) is surjective, since for every y in the nonnegative real codomain Y, there is at least one x in the real domain X such that Template:Nowrap beginx2 = yTemplate:Nowrap end.
- The natural logarithm function ln : (0, +∞) → R is a surjective and even bijective (mapping from the set of positive real numbers to the set of all real numbers). Its inverse, the exponential function, if defined with the set of real numbers as the domain, is not surjective (as its range is the set of positive real numbers).
- The matrix exponential is not surjective when seen as a map from the space of all n×n matrices to itself. It is, however, usually defined as a map from the space of all n×n matrices to the general linear group of degree n (that is, the group of all n×n invertible matrices). Under this definition, the matrix exponential is surjective for complex matrices, although still not surjective for real matrices.
- The projection from a cartesian product A × B to one of its factors is surjective, unless the other factor is empty.
- In a 3D video game, vectors are projected onto a 2D flat screen by means of a surjective function.

Properties
A function is bijective if and only if it is both surjective and injective.
If (as is often done) a function is identified with its graph, then surjectivity is not a property of the function itself, but rather a property of the mapping.[7] This is, the function together with its codomain. Unlike injectivity, surjectivity cannot be read off of the graph of the function alone.
Surjections as right invertible functions
The function Template:Nowrap is said to be a right inverse of the function Template:Nowrap if Template:Nowrap beginf(g(y)) = yTemplate:Nowrap end for every y in Y (g can be undone by f). In other words, g is a right inverse of f if the composition Template:Nowrap of g and f in that order is the identity function on the domain Y of g. The function g need not be a complete inverse of f because the composition in the other order, Template:Nowrap, may not be the identity function on the domain X of f. In other words, f can undo or "reverse" g, but cannot necessarily be reversed by it.
Every function with a right inverse is necessarily a surjection. The proposition that every surjective function has a right inverse is equivalent to the axiom of choice.
If Template:Nowrap is surjective and B is a subset of Y, then Template:Nowrap beginf(f −1(B)) = BTemplate:Nowrap end. Thus, B can be recovered from its preimage Template:Nowrap.
For example, in the first illustration above, there is some function g such that g(C) = 4. There is also some function f such that f(4) = C. It doesn't matter that g(C) can also equal 3; it only matters that f "reverses" g.
Another surjective function. (This one happens to be a bijection)
A non-surjective function. (This one happens to be an injection)
Surjections as epimorphisms
A function Template:Nowrap is surjective if and only if it is right-cancellative:[8] given any functions Template:Nowrap, whenever Template:Nowrap beging o f = h o fTemplate:Nowrap end, then Template:Nowrap beging = hTemplate:Nowrap end. This property is formulated in terms of functions and their composition and can be generalized to the more general notion of the morphisms of a category and their composition. Right-cancellative morphisms are called epimorphisms. Specifically, surjective functions are precisely the epimorphisms in the category of sets. The prefix epi is derived from the Greek preposition ἐπί meaning over, above, on.
Any morphism with a right inverse is an epimorphism, but the converse is not true in general. A right inverse g of a morphism f is called a section of f. A morphism with a right inverse is called a split epimorphism.
Surjections as binary relations
Any function with domain X and codomain Y can be seen as a left-total and right-unique binary relation between X and Y by identifying it with its function graph. A surjective function with domain X and codomain Y is then a binary relation between X and Y that is right-unique and both left-total and right-total.
Cardinality of the domain of a surjection
The cardinality of the domain of a surjective function is greater than or equal to the cardinality of its codomain: If Template:Nowrap is a surjective function, then X has at least as many elements as Y, in the sense of cardinal numbers. (The proof appeals to the axiom of choice to show that a function Template:Nowrap satisfying f(g(y)) = y for all y in Y exists. g is easily seen to be injective, thus the formal definition of |Y| ≤ |X| is satisfied.)
Specifically, if both X and Y are finite with the same number of elements, then Template:Nowrap is surjective if and only if f is injective.
Given two sets X and Y, the notation Template:Nowrap is used to say that either X is empty or that there is a surjection from Y onto X. Using the axiom of choice one can show that Template:Nowrap and Template:Nowrap together imply that Template:Nowrap begin|Y| = |X|,Template:Nowrap end a variant of the Schröder–Bernstein theorem.
Composition and decomposition
The composition of surjective functions is always surjective: If f and g are both surjective, and the codomain of g is equal to the domain of f, then Template:Nowrap is surjective. Conversely, if Template:Nowrap is surjective, then f is surjective (but g, the function applied first, need not be). These properties generalize from surjections in the category of sets to any epimorphisms in any category.
Any function can be decomposed into a surjection and an injection: For any function Template:Nowrap there exist a surjection Template:Nowrap and an injection Template:Nowrap such that Template:Nowrap beginh = g o fTemplate:Nowrap end. To see this, define Y to be the set of preimages Template:Nowrap where z is in Template:Nowrap. These preimages are disjoint and partition X. Then f carries each x to the element of Y which contains it, and g carries each element of Y to the point in Z to which h sends its points. Then f is surjective since it is a projection map, and g is injective by definition.
Induced surjection and induced bijection
Any function induces a surjection by restricting its codomain to its range. Any surjective function induces a bijection defined on a quotient of its domain by collapsing all arguments mapping to a given fixed image. More precisely, every surjection Template:Nowrap can be factored as a projection followed by a bijection as follows. Let A/~ be the equivalence classes of A under the following equivalence relation: x ~ y if and only if f(x) = f(y). Equivalently, A/~ is the set of all preimages under f. Let P(~) : A → A/~ be the projection map which sends each x in A to its equivalence class [x]~, and let fP : A/~ → B be the well-defined function given by fP([x]~) = f(x). Then f = fP o P(~).
Space of surjections
Given fixed A and B, one can form the set of surjections A ↠ B. The cardinality of this set is one of the twelve aspects of Rota's Twelvefold way, and is given by , where denotes a Stirling number of the second kind.
Resources
- Course Textbook, pages 154-164
Licensing
Content obtained and/or adapted from:
- Surjective function, Wikipedia under a CC BY-SA license













