Unions and Intersections of Sets

Union of two sets:
$~A\cup B$

Union of three sets:
$~A\cup B\cup C$

The union of A, B, C, D, and E is everything except the white area.

Union of two sets

The union of two sets A and B is the set of elements which are in A, in B, or in both A and B. In symbols,

$A\cup B=\{x:x\in A{\text{ or }}x\in B\}$.

For example, if A = {1, 3, 5, 7} and B = {1, 2, 4, 6, 7} then A ∪ B = {1, 2, 3, 4, 5, 6, 7}. A more elaborate example (involving two infinite sets) is:

A = {x is an even integer larger than 1}

B = {x is an odd integer larger than 1}

$A\cup B=\{2,3,4,5,6,\dots \}$

As another example, the number 9 is not contained in the union of the set of prime numbers {2, 3, 5, 7, 11, ...} and the set of even numbers {2, 4, 6, 8, 10, ...}, because 9 is neither prime nor even.

Sets cannot have duplicate elements, so the union of the sets {1, 2, 3} and {2, 3, 4} is {1, 2, 3, 4}. Multiple occurrences of identical elements have no effect on the cardinality of a set or its contents.

Algebraic properties

Binary union is an associative operation; that is, for any sets A, B, and C,

$A\cup (B\cup C)=(A\cup B)\cup C.$

Thus the parentheses may be omitted without ambiguity: either of the above can be written as A ∪ B ∪ C. Also, union is commutative, so the sets can be written in any order. The empty set is an identity element for the operation of union. That is, A ∪ ∅ = A, for any set A. Also, the union operation is idempotent: A ∪ A = A. All these properties follow from analogous facts about logical disjunction.

Intersection distributes over union

$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

and union distributes over intersection

$A\cup (B\cap C)=(A\cup B)\cap (A\cup C).$

The power set of a set U, together with the operations given by union, intersection, and complementation, is a Boolean algebra. In this Boolean algebra, union can be expressed in terms of intersection and complementation by the formula

$A\cup B=\left(A^{\text{c}}\cap B^{\text{c}}\right)^{\text{c}},$

where the superscript ${}^{\text{c}}$ denotes the complement in the universal set U.

Finite unions

One can take the union of several sets simultaneously. For example, the union of three sets A, B, and C contains all elements of A, all elements of B, and all elements of C, and nothing else. Thus, x is an element of A ∪ B ∪ C if and only if x is in at least one of A, B, and C.

A finite union is the union of a finite number of sets; the phrase does not imply that the union set is a finite set.

Arbitrary unions

The most general notion is the union of an arbitrary collection of sets, sometimes called an infinitary union. If M is a set or class whose elements are sets, then x is an element of the union of M if and only if there is at least one element A of M such that x is an element of A. In symbols:

$x\in \bigcup \mathbf {M} \iff \exists A\in \mathbf {M} ,\ x\in A.$

This idea subsumes the preceding sections—for example, A ∪ B ∪ C is the union of the collection {A, B, C}. Also, if M is the empty collection, then the union of M is the empty set.

Notations

The notation for the general concept can vary considerably. For a finite union of sets $S_{1},S_{2},S_{3},\dots ,S_{n}$ one often writes $S_{1}\cup S_{2}\cup S_{3}\cup \dots \cup S_{n}$ or $\bigcup _{i=1}^{n}S_{i}$. Various common notations for arbitrary unions include $\bigcup \mathbf {M}$, $\bigcup _{A\in \mathbf {M} }A$, and $\bigcup _{i\in I}A_{i}$. The last of these notations refers to the union of the collection $\left\{A_{i}:i\in I\right\}$, where I is an index set and $A_{i}$ is a set for every $i\in I$. In the case that the index set I is the set of natural numbers, one uses the notation $\bigcup _{i=1}^{\infty }A_{i}$, which is analogous to that of the infinite sums in series.

When the symbol "∪" is placed before other symbols (instead of between them), it is usually rendered as a larger size.

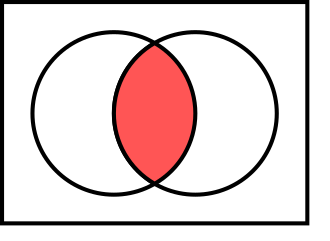
Intersection of two sets

The intersection of two sets $A$ and $B,$ represented by circles. $A\cap B$ is in red.

The intersection of two sets $A$ and $B,$ denoted by $A\cap B,$ is the set containing all elements of $A$ that also belong to $B$ or equivalently, all elements of $B$ that also belong to $A.$

Notation and terminology

Intersection is written using the symbol "$\cap$" between the terms; that is, in infix notation. For example:

$$\{1,2,3\}\cap \{2,3,4\}=\{2,3\}$$

$$\{1,2,3\}\cap \{4,5,6\}=\varnothing$$

$$\mathbb {Z} \cap \mathbb {N} =\mathbb {N}$$

$$\{x\in \mathbb {R} :x^{2}=1\}\cap \mathbb {N} =\{1\}$$

The intersection of more than two sets (generalized intersection) can be written as:

$$\bigcap _{i=1}^{n}A_{i}$$

which is similar to capital-sigma notation.

For an explanation of the symbols used in this article, refer to the table of mathematical symbols.

Definition

Intersection of three sets:
$~A\cap B\cap C$

Intersections of the unaccented modern Greek, Latin, and Cyrillic scripts, considering only the shapes of the letters and ignoring their pronunciation

Example of an intersection with sets

The intersection of two sets $A$ and $B,$ denoted by $A\cap B$, is the set of all objects that are members of both the sets $A$ and $B.$ In symbols:

$$A\cap B=\{x:x\in A{\text{ and }}x\in B\}.$$

That is, $x$ is an element of the intersection $A\cap B$ if and only if $x$ is both an element of $A$ and an element of $B.$

For example:

• The intersection of the sets {1, 2, 3} and {2, 3, 4} is {2, 3}.
• The number 9 is not in the intersection of the set of prime numbers {2, 3, 5, 7, 11, ...} and the set of odd numbers {1, 3, 5, 7, 9, 11, ...}, because 9 is not prime.

Intersecting and disjoint sets

We say that $A$ intersects (meets) $B$ if there exists some $x$ that is an element of both $A$ and $B,$ in which case we also say that \\$A$ intersects (meets) $B$ at $x$. Equivalently, $A$ intersects $B$ if their intersection $A\cap B$ is an inhabited set, meaning that there exists some $x$ such that $x\in A\cap B.$

We say that $A$ and $B$ are disjoint if $A$ does not intersect $B.$ In plain language, they have no elements in common. $A$ and $B$ are disjoint if their intersection is empty, denoted $A\cap B=\varnothing .$

For example, the sets $\{1,2\}$ and $\{3,4\}$ are disjoint, while the set of even numbers intersects the set of multiples of 3 at the multiples of 6.

Algebraic properties

Binary intersection is an associative operation; that is, for any sets $A,B,$ and $C,$ one has

$$A\cap (B\cap C)=(A\cap B)\cap C.$$

Thus the parentheses may be omitted without ambiguity: either of the above can be written as $A\cap B\cap C$. Intersection is also commutative. That is, for any $A$ and $B,$ one has

$$A\cap B=B\cap A.$$

The intersection of any set with the empty set results in the empty set; that is, that for any set $A$,

$$A\cap \emptyset =\emptyset$$

Also, the intersection operation is idempotent; that is, any set $A$ satisfies that $A\cap A=A$. All these properties follow from analogous facts about logical conjunction.

Intersection distributes over union and union distributes over intersection. That is, for any sets $A,B,$ and $C,$ one has

$${\begin{aligned}A\cap (B\cup C)=(A\cap B)\cup (A\cap C)\\A\cup (B\cap C)=(A\cup B)\cap (A\cup C)\end{aligned}}$$

Inside a universe $U,$ one may define the complement $A^{c}$ of $A$ to be the set of all elements of $U$ not in $A.$ Furthermore, the intersection of $A$ and $B$ may be written as the complement of the union of their complements, derived easily from de Morgan's laws:

$$A\cap B=\left(A^{c}\cup B^{c}\right)^{c}$$

Arbitrary intersections

The most general notion is the intersection of an arbitrary nonempty collection of sets. If $M$ is a nonempty set whose elements are themselves sets, then $x$ is an element of the intersection of $M$ if and only if for every element $A$ of $M,$ $x$ is an element of $A.$ In symbols:

$$\left(x\in \bigcap _{A\in M}A\right)\Leftrightarrow \left(\forall A\in M,\ x\in A\right).$$

The notation for this last concept can vary considerably. Set theorists will sometimes write "$\cap M$", while others will instead write "$\cap _{A\in M}A$". The latter notation can be generalized to "$\cap _{i\in I}A_{i}$", which refers to the intersection of the collection $\left\{A_{i}:i\in I\right\}.$ Here $I$ is a nonempty set, and $A_{i}$ is a set for every $i\in I.$

In the case that the index set $I$ is the set of natural numbers, notation analogous to that of an infinite product may be seen:

$$\bigcap _{i=1}^{\infty }A_{i}.$$

When formatting is difficult, this can also be written "$A_{1}\cap A_{2}\cap A_{3}\cap \cdots$". This last example, an intersection of countably many sets, is actually very common; for an example, see the article on σ-algebras.

Nullary intersection

Conjunctions of the arguments in parentheses

The conjunction of no argument is the tautology (compare: empty product); accordingly the intersection of no set is the universe.

Note that in the previous section, we excluded the case where $M$ was the empty set ($\varnothing$). The reason is as follows: The intersection of the collection $M$ is defined as the set (see set-builder notation)

$$\bigcap _{A\in M}A=\{x:{\text{ for all }}A\in M,x\in A\}.$$

If $M$ is empty, there are no sets $A$ in $M,$ so the question becomes "which $x$'s satisfy the stated condition?" The answer seems to be every possible $x$. When $M$ is empty, the condition given above is an example of a vacuous truth. So the intersection of the empty family should be the universal set (the identity element for the operation of intersection), but in standard (ZF) set theory, the universal set does not exist.

In type theory however, $x$ is of a prescribed type $\tau ,$ so the intersection is understood to be of type $\mathrm {set} \ \tau$ (the type of sets whose elements are in $\tau$), and we can define $\bigcap _{A\in \emptyset }A$ to be the universal set of $\mathrm {set} \ \tau$ (the set whose elements are exactly all terms of type $\tau$).

Licensing

Content obtained and/or adapted from:

• Union (set theory) under a CC BY-SA license
• Intersection (set theory) under a CC BY-SA license