Difference between revisions of "Perimeter Area"
| Line 1: | Line 1: | ||
| + | = Perimeter = | ||
| + | [[File:Perimiters.svg|thumb|250px|Perimeter is the distance around a two dimensional shape, a measurement of the distance around something; the length of the boundary.]] | ||
| + | |||
| + | A '''perimeter''' is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference. | ||
| + | |||
| + | Calculating the perimeter has several practical applications. A calculated perimeter is the length of fence required to surround a yard or garden. The perimeter of a wheel/circle (its circumference) describes how far it will roll in one revolution. Similarly, the amount of string wound around a spool is related to the spool's perimeter; if the length of the string was exact, it would equal the perimeter. | ||
| + | |||
| + | == Formulas == | ||
| + | {| class="wikitable sortable mw-collapsible" | ||
| + | |+ | ||
| + | ! shape !! formula || variables | ||
| + | |- | ||
| + | | circle || <math>2 \pi r = \pi d</math> || where <math>r</math> is the radius of the circle and <math>d</math> is the diameter. | ||
| + | |- | ||
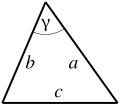
| + | | triangle || <math>a + b + c\,</math> || where <math>a</math>, <math>b</math> and <math>c</math> are the lengths of the sides of the triangle. | ||
| + | |- | ||
| + | | square/rhombus || <math>4a</math> || where <math>a</math> is the side length. | ||
| + | |- | ||
| + | | rectangle || <math>2(l+w)</math> || where <math>l</math> is the length and <math>w</math> is the width. | ||
| + | |- | ||
| + | | equilateral polygon || <math>n \times a\,</math> || where <math>n</math> is the number of sides and <math>a</math> is the length of one of the sides. | ||
| + | |- | ||
| + | | regular polygon || <math>2nb \sin\left(\frac{\pi}{n}\right)</math> || where <math>n</math> is the number of sides and <math>b</math> is the distance between center of the polygon and one of the vertices of the polygon. | ||
| + | |- | ||
| + | | general polygon || <math>a_1 + a_2 + a_3 + \cdots + a_n = \sum_{i=1}^n a_i</math> || where <math>a_{i}</math> is the length of the <math>i</math>-th (1st, 2nd, 3rd ... ''n''th) side of an ''n''-sided polygon. | ||
| + | |} | ||
| + | [[File:Herzkurve2.svg|thumb|upright=1.0|Cardoid <math>\gamma:[0,2\pi]\rightarrow \mathbb{R}^2 </math><br/>(drawing with <math>a=1</math>)<br/><math>x(t) = 2 a \cos(t) (1 + \cos(t))</math><br/><math>y(t) = 2 a \sin(t) (1 + \cos (t))</math><br/><math>L = \int\limits_0^{2\pi}\sqrt{x'(t)^2+y'(t)^2}\,\mathrm dt=16a</math>]] | ||
| + | The perimeter is the distance around a shape. Perimeters for more general shapes can be calculated, as any path, with <math>\int_0^L \mathrm{d}s</math>, where <math>L</math> is the length of the path and <math>ds</math> is an infinitesimal line element. Both of these must be replaced by algebraic forms in order to be practically calculated. If the perimeter is given as a closed piecewise smooth plane curve <math> \gamma:[a,b]\rightarrow \mathbb{R}^2</math> with | ||
| + | :<math> \gamma(t)=\begin{pmatrix}x(t)\\y(t)\end{pmatrix}</math> | ||
| + | then its length <math>L</math> can be computed as follows: | ||
| + | : <math>L = \int\limits_a^b\sqrt{x'(t)^2+y'(t)^2}\,\mathrm dt</math> | ||
| + | |||
| + | A generalized notion of perimeter, which includes hypersurfaces bounding volumes in <math>n</math>-dimensional Euclidean spaces, is described by the theory of Caccioppoli sets. | ||
| + | |||
| + | ==Polygons== | ||
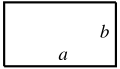
| + | [[File:PerimeterRectangle.svg|thumb|Perimeter of a rectangle.]] | ||
| + | |||
| + | Polygons are fundamental to determining perimeters, not only because they are the simplest shapes but also because the perimeters of many shapes are calculated by approximating them with sequences of polygons tending to these shapes. The first mathematician known to have used this kind of reasoning is Archimedes, who approximated the perimeter of a circle by surrounding it with regular polygons. | ||
| + | |||
| + | The perimeter of a polygon equals the sum of the lengths of its sides (edges). In particular, the perimeter of a rectangle of width <math>w</math> and length <math>\ell</math> equals <math>2w + 2\ell.</math> | ||
| + | |||
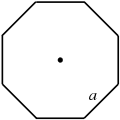
| + | An equilateral polygon is a polygon which has all sides of the same length (for example, a rhombus is a 4-sided equilateral polygon). To calculate the perimeter of an equilateral polygon, one must multiply the common length of the sides by the number of sides. | ||
| + | |||
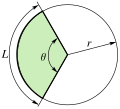
| + | A regular polygon may be characterized by the number of its sides and by its circumradius, that is to say, the constant distance between its centre and each of its vertices. The length of its sides can be calculated using trigonometry. If {{math|''R''}} is a regular polygon's radius and {{math|''n''}} is the number of its sides, then its perimeter is | ||
| + | :<math>2nR \sin\left(\frac{180^{\circ}}{n}\right).</math> | ||
| + | |||
| + | A splitter of a triangle is a cevian (a segment from a vertex to the opposite side) that divides the perimeter into two equal lengths, this common length being called the semiperimeter of the triangle. The three splitters of a triangle all intersect each other at the Nagel point of the triangle. | ||
| + | |||
| + | A cleaver of a triangle is a segment from the midpoint of a side of a triangle to the opposite side such that the perimeter is divided into two equal lengths. The three cleavers of a triangle all intersect each other at the triangle's Spieker center. | ||
| + | |||
| + | ==Circumference of a circle== | ||
| + | [[File:Pi-unrolled-720.gif|right|300px|thumb|If the diameter of a circle is 1, its circumference equals <math> \pi </math>.]] | ||
| + | |||
| + | The perimeter of a circle, often called the circumference, is proportional to its diameter and its radius. That is to say, there exists a constant number pi, <math> \pi </math> (the Greek ''p'' for perimeter), such that if {{math|''P''}} is the circle's perimeter and {{math|''D''}} its diameter then, | ||
| + | :<math>P = \pi\cdot{D}.\!</math> | ||
| + | |||
| + | In terms of the radius {{math|''r''}} of the circle, this formula becomes, | ||
| + | |||
| + | :<math>P=2\pi\cdot r.</math> | ||
| + | |||
| + | To calculate a circle's perimeter, knowledge of its radius or diameter and the number <math> \pi </math> suffices. The problem is that <math> \pi </math> is not rationa (it cannot be expressed as the quotient of two integers), nor is it algebraic (it is not a root of a polynomial equation with rational coefficients). So, obtaining an accurate approximation of <math> \pi </math> is important in the calculation. The computation of the digits of <math> \pi </math> is relevant to many fields, such as mathematical analysis, algorithmics and computer science. | ||
| + | |||
| + | == Perception of perimeter== | ||
| + | [[File:Hexaflake.gif|thumb|left|upright=0.6|The more one cuts this shape, the lesser the area and the greater the perimeter. The convex hull remains the same.]] | ||
| + | [[File:Neuf Brisach.jpg|thumb|The Neuf-Brisach fortification perimeter is complicated. The shortest path around it is along its convex hull.]] | ||
| + | |||
| + | The perimeter and the area are two main measures of geometric figures. Confusing them is a common error, as well as believing that the greater one of them is, the greater the other must be. Indeed, a commonplace observation is that an enlargement (or a reduction) of a shape make its area grow (or decrease) as well as its perimeter. For example, if a field is drawn on a 1/{{formatnum:10000}} scale map, the actual field perimeter can be calculated multiplying the drawing perimeter by {{formatnum:10000}}. The real area is {{formatnum:10000}}<sup>2</sup> times the area of the shape on the map. Nevertheless, there is no relation between the area and the perimeter of an ordinary shape. For example, the perimeter of a rectangle of width 0.001 and length 1000 is slightly above 2000, while the perimeter of a rectangle of width 0.5 and length 2 is 5. Both areas equal to 1. | ||
| + | |||
| + | Proclus (5th century) reported that Greek peasants "fairly" parted fields relying on their perimeters. However, a field's production is proportional to its area, not to its perimeter, so many naive peasants may have gotten fields with long perimeters but small areas (thus, few crops). | ||
| + | |||
| + | If one removes a piece from a figure, its area decreases but its perimeter may not. In the case of very irregular shapes, confusion between the perimeter and the convex hull may arise. The convex hull of a figure may be visualized as the shape formed by a rubber band stretched around it. In the animated picture on the left, all the figures have the same convex hull; the big, first hexagon. | ||
| + | |||
| + | == Isoperimetry == | ||
| + | |||
| + | The isoperimetric problem is to determine a figure with the largest area, amongst those having a given perimeter. The solution is intuitive; it is the circle. In particular, this can be used to explain why drops of fat on a broth surface are circular. | ||
| + | |||
| + | This problem may seem simple, but its mathematical proof requires some sophisticated theorems. The isoperimetric problem is sometimes simplified by restricting the type of figures to be used. In particular, to find the quadrilateral, or the triangle, or another particular figure, with the largest area amongst those with the same shape having a given perimeter. The solution to the quadrilateral isoperimetric problem is the square, and the solution to the triangle problem is the equilateral triangle. In general, the polygon with {{math|''n''}} sides having the largest area and a given perimeter is the regular polygon, which is closer to being a circle than is any irregular polygon with the same number of sides. | ||
| + | |||
| + | ==Etymology== | ||
| + | The word comes from the Greek περίμετρος ''perimetros'' from περί ''peri'' "around" and μέτρον ''metron'' "measure". | ||
| + | |||
= Area = | = Area = | ||
| Line 323: | Line 404: | ||
The ratio of the area to the square of the perimeter of an equilateral triangle, <math>\frac{1}{12\sqrt{3}},</math> is larger than that for any other triangle. | The ratio of the area to the square of the perimeter of an equilateral triangle, <math>\frac{1}{12\sqrt{3}},</math> is larger than that for any other triangle. | ||
| − | + | = Licensing = | |
Content obtained and/or adapted from: | Content obtained and/or adapted from: | ||
* [https://en.wikipedia.org/wiki/Perimeter Perimeter, Wikipedia] under a CC BY-SA license | * [https://en.wikipedia.org/wiki/Perimeter Perimeter, Wikipedia] under a CC BY-SA license | ||
* [https://en.wikipedia.org/wiki/Area Area, Wikipedia] under a CC BY-SA license | * [https://en.wikipedia.org/wiki/Area Area, Wikipedia] under a CC BY-SA license | ||
Latest revision as of 22:09, 15 December 2021
Contents
Perimeter
A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimeter has several practical applications. A calculated perimeter is the length of fence required to surround a yard or garden. The perimeter of a wheel/circle (its circumference) describes how far it will roll in one revolution. Similarly, the amount of string wound around a spool is related to the spool's perimeter; if the length of the string was exact, it would equal the perimeter.
Formulas
| shape | formula | variables |
|---|---|---|
| circle | where is the radius of the circle and is the diameter. | |
| triangle | where , and are the lengths of the sides of the triangle. | |
| square/rhombus | where is the side length. | |
| rectangle | where is the length and is the width. | |
| equilateral polygon | where is the number of sides and is the length of one of the sides. | |
| regular polygon | where is the number of sides and is the distance between center of the polygon and one of the vertices of the polygon. | |
| general polygon | where is the length of the -th (1st, 2nd, 3rd ... nth) side of an n-sided polygon. |
The perimeter is the distance around a shape. Perimeters for more general shapes can be calculated, as any path, with , where is the length of the path and is an infinitesimal line element. Both of these must be replaced by algebraic forms in order to be practically calculated. If the perimeter is given as a closed piecewise smooth plane curve with
then its length can be computed as follows:
A generalized notion of perimeter, which includes hypersurfaces bounding volumes in -dimensional Euclidean spaces, is described by the theory of Caccioppoli sets.
Polygons
Polygons are fundamental to determining perimeters, not only because they are the simplest shapes but also because the perimeters of many shapes are calculated by approximating them with sequences of polygons tending to these shapes. The first mathematician known to have used this kind of reasoning is Archimedes, who approximated the perimeter of a circle by surrounding it with regular polygons.
The perimeter of a polygon equals the sum of the lengths of its sides (edges). In particular, the perimeter of a rectangle of width and length equals
An equilateral polygon is a polygon which has all sides of the same length (for example, a rhombus is a 4-sided equilateral polygon). To calculate the perimeter of an equilateral polygon, one must multiply the common length of the sides by the number of sides.
A regular polygon may be characterized by the number of its sides and by its circumradius, that is to say, the constant distance between its centre and each of its vertices. The length of its sides can be calculated using trigonometry. If R is a regular polygon's radius and n is the number of its sides, then its perimeter is
A splitter of a triangle is a cevian (a segment from a vertex to the opposite side) that divides the perimeter into two equal lengths, this common length being called the semiperimeter of the triangle. The three splitters of a triangle all intersect each other at the Nagel point of the triangle.
A cleaver of a triangle is a segment from the midpoint of a side of a triangle to the opposite side such that the perimeter is divided into two equal lengths. The three cleavers of a triangle all intersect each other at the triangle's Spieker center.
Circumference of a circle
The perimeter of a circle, often called the circumference, is proportional to its diameter and its radius. That is to say, there exists a constant number pi, (the Greek p for perimeter), such that if P is the circle's perimeter and D its diameter then,
In terms of the radius r of the circle, this formula becomes,
To calculate a circle's perimeter, knowledge of its radius or diameter and the number suffices. The problem is that is not rationa (it cannot be expressed as the quotient of two integers), nor is it algebraic (it is not a root of a polynomial equation with rational coefficients). So, obtaining an accurate approximation of is important in the calculation. The computation of the digits of is relevant to many fields, such as mathematical analysis, algorithmics and computer science.
Perception of perimeter
The perimeter and the area are two main measures of geometric figures. Confusing them is a common error, as well as believing that the greater one of them is, the greater the other must be. Indeed, a commonplace observation is that an enlargement (or a reduction) of a shape make its area grow (or decrease) as well as its perimeter. For example, if a field is drawn on a 1/10,000 scale map, the actual field perimeter can be calculated multiplying the drawing perimeter by 10,000. The real area is 10,0002 times the area of the shape on the map. Nevertheless, there is no relation between the area and the perimeter of an ordinary shape. For example, the perimeter of a rectangle of width 0.001 and length 1000 is slightly above 2000, while the perimeter of a rectangle of width 0.5 and length 2 is 5. Both areas equal to 1.
Proclus (5th century) reported that Greek peasants "fairly" parted fields relying on their perimeters. However, a field's production is proportional to its area, not to its perimeter, so many naive peasants may have gotten fields with long perimeters but small areas (thus, few crops).
If one removes a piece from a figure, its area decreases but its perimeter may not. In the case of very irregular shapes, confusion between the perimeter and the convex hull may arise. The convex hull of a figure may be visualized as the shape formed by a rubber band stretched around it. In the animated picture on the left, all the figures have the same convex hull; the big, first hexagon.
Isoperimetry
The isoperimetric problem is to determine a figure with the largest area, amongst those having a given perimeter. The solution is intuitive; it is the circle. In particular, this can be used to explain why drops of fat on a broth surface are circular.
This problem may seem simple, but its mathematical proof requires some sophisticated theorems. The isoperimetric problem is sometimes simplified by restricting the type of figures to be used. In particular, to find the quadrilateral, or the triangle, or another particular figure, with the largest area amongst those with the same shape having a given perimeter. The solution to the quadrilateral isoperimetric problem is the square, and the solution to the triangle problem is the equilateral triangle. In general, the polygon with n sides having the largest area and a given perimeter is the regular polygon, which is closer to being a circle than is any irregular polygon with the same number of sides.
Etymology
The word comes from the Greek περίμετρος perimetros from περί peri "around" and μέτρον metron "measure".
Area
Area is the quantity that expresses the extent of a two-dimensional region, shape, or planar lamina, in the plane. Surface area is its analog on the two-dimensional surface of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analog of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept).
The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area of a square whose sides are one metre long. A shape with an area of three square metres would have the same area as three such squares. In mathematics, the unit square is defined to have area one, and the area of any other shape or surface is a dimensionless real number.
There are several well-known formulas for the areas of simple shapes such as triangles, rectangles, and circles. Using these formulas, the area of any polygon can be found by dividing the polygon into triangles. For shapes with curved boundary, calculus is usually required to compute the area. Indeed, the problem of determining the area of plane figures was a major motivation for the historical development of calculus.
For a solid shape such as a sphere, cone, or cylinder, the area of its boundary surface is called the surface area. Formulas for the surface areas of simple shapes were computed by the ancient Greeks, but computing the surface area of a more complicated shape usually requires multivariable calculus.
Area plays an important role in modern mathematics. In addition to its obvious importance in geometry and calculus, area is related to the definition of determinants in linear algebra, and is a basic property of surfaces in differential geometry. In analysis, the area of a subset of the plane is defined using Lebesgue measure, though not every subset is measurable. In general, area in higher mathematics is seen as a special case of volume for two-dimensional regions.
Area can be defined through the use of axioms, defining it as a function of a collection of certain plane figures to the set of real numbers. It can be proved that such a function exists.
Formal definition
An approach to defining what is meant by "area" is through axioms. "Area" can be defined as a function from a collection M of a special kinds of plane figures (termed measurable sets) to the set of real numbers, which satisfies the following properties:
- For all S in M, a(S) ≥ 0.
- If S and T are in M then so are S ∪ T and S ∩ T, and also a(S∪T) = a(S) + a(T) − a(S∩T).
- If S and T are in M with S ⊆ T then T − S is in M and a(T−S) = a(T) − a(S).
- If a set S is in M and S is congruent to T then T is also in M and a(S) = a(T).
- Every rectangle R is in M. If the rectangle has length h and breadth k then a(R) = hk.
- Let Q be a set enclosed between two step regions S and T. A step region is formed from a finite union of adjacent rectangles resting on a common base, i.e. S ⊆ Q ⊆ T. If there is a unique number c such that a(S) ≤ c ≤ a(T) for all such step regions S and T, then a(Q) = c.
It can be proved that such an area function actually exists.
Units
Every unit of length has a corresponding unit of area, namely the area of a square with the given side length. Thus areas can be measured in square metres (m2), square centimetres (cm2), square millimetres (mm2), square kilometres (km2), square feet (ft2), square yards (yd2), square miles (mi2), and so forth. Algebraically, these units can be thought of as the squares of the corresponding length units.
The SI unit of area is the square metre, which is considered an SI derived unit.
Conversions
Calculation of the area of a square whose length and width are 1 metre would be:
1 metre × 1 metre = 1 m2
and so, a rectangle with different sides (say length of 3 metres and width of 2 metres) would have an area in square units that can be calculated as:
3 metres × 2 metres = 6 m2. This is equivalent to 6 million square millimetres. Other useful conversions are:
- 1 square kilometre = 1,000,000 square metres
- 1 square metre = 10,000 square centimetres = 1,000,000 square millimetres
- 1 square centimetre = 100 square millimetres.
Non-metric units
In non-metric units, the conversion between two square units is the square of the conversion between the corresponding length units.
- 1 foot = 12 inches,
the relationship between square feet and square inches is
- 1 square foot = 144 square inches,
where 144 = 122 = 12 × 12. Similarly:
- 1 square yard = 9 square feet
- 1 square mile = 3,097,600 square yards = 27,878,400 square feet
In addition, conversion factors include:
- 1 square inch = 6.4516 square centimetres
- 1 square foot = 0.092 903 04 square metres
- 1 square yard = 0.836 127 36 square metres
- 1 square mile = 2.589 988 110 336 square kilometres
Other units including historical
There are several other common units for area. The are was the original unit of area in the metric system, with:
- 1 are = 100 square metres
Though the are has fallen out of use, the hectare is still commonly used to measure land:
- 1 hectare = 100 ares = 10,000 square metres = 0.01 square kilometres
Other uncommon metric units of area include the tetrad, the hectad, and the myriad.
The acre is also commonly used to measure land areas, where
- 1 acre = 4,840 square yards = 43,560 square feet.
An acre is approximately 40% of a hectare.
On the atomic scale, area is measured in units of barns, such that:
- 1 barn = 10−28 square meters.
The barn is commonly used in describing the cross-sectional area of interaction in nuclear physics.
In India,
- 20 dhurki = 1 dhur
- 20 dhur = 1 khatha
- 20 khata = 1 bigha
- 32 khata = 1 acre
Area formulas
Polygon formulas
For a non-self-intersecting (simple) polygon, the Cartesian coordinates (i=0, 1, ..., n-1) of whose n vertices are known, the area is given by the surveyor's formula:
where when i=n-1, then i+1 is expressed as modulus n and so refers to 0.
Rectangles
The most basic area formula is the formula for the area of a rectangle. Given a rectangle with length l and width w, the formula for the area is:
- A = lw (rectangle).
That is, the area of the rectangle is the length multiplied by the width. As a special case, as l = w in the case of a square, the area of a square with side length s is given by the formula:
- A = s2 (square).
The formula for the area of a rectangle follows directly from the basic properties of area, and is sometimes taken as a definition or axiom. On the other hand, if geometry is developed before arithmetic, this formula can be used to define multiplication of real numbers.
Dissection, parallelograms, and triangles
Most other simple formulas for area follow from the method of dissection. This involves cutting a shape into pieces, whose areas must sum to the area of the original shape.
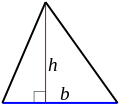
For an example, any parallelogram can be subdivided into a trapezoid and a right triangle, as shown in figure to the left. If the triangle is moved to the other side of the trapezoid, then the resulting figure is a rectangle. It follows that the area of the parallelogram is the same as the area of the rectangle:
- A = bh (parallelogram).
However, the same parallelogram can also be cut along a diagonal into two congruent triangles, as shown in the figure to the right. It follows that the area of each triangle is half the area of the parallelogram:
- (triangle).
Similar arguments can be used to find area formulas for the trapezoid as well as more complicated polygons.
Area of curved shapes
Circles
The formula for the area of a circle (more properly called the area enclosed by a circle or the area of a disk) is based on a similar method. Given a circle of radius r, it is possible to partition the circle into sectors, as shown in the figure to the right. Each sector is approximately triangular in shape, and the sectors can be rearranged to form an approximate parallelogram. The height of this parallelogram is r, and the width is half the circumference of the circle, or πr. Thus, the total area of the circle is πr2:
- A = πr2 (circle).
Though the dissection used in this formula is only approximate, the error becomes smaller and smaller as the circle is partitioned into more and more sectors. The limit of the areas of the approximate parallelograms is exactly πr2, which is the area of the circle.
This argument is actually a simple application of the ideas of calculus. In ancient times, the method of exhaustion was used in a similar way to find the area of the circle, and this method is now recognized as a precursor to integral calculus. Using modern methods, the area of a circle can be computed using a definite integral:
Ellipses
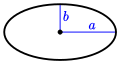
The formula for the area enclosed by an ellipse is related to the formula of a circle; for an ellipse with semi-major and semi-minor axes x and y the formula is:
Surface area
Most basic formulas for surface area can be obtained by cutting surfaces and flattening them out. For example, if the side surface of a cylinder (or any prism) is cut lengthwise, the surface can be flattened out into a rectangle. Similarly, if a cut is made along the side of a cone, the side surface can be flattened out into a sector of a circle, and the resulting area computed.
The formula for the surface area of a sphere is more difficult to derive: because a sphere has nonzero Gaussian curvature, it cannot be flattened out. The formula for the surface area of a sphere was first obtained by Archimedes in his work On the Sphere and Cylinder. The formula is:
- A = 4πr2 (sphere),
where r is the radius of the sphere. As with the formula for the area of a circle, any derivation of this formula inherently uses methods similar to calculus.
General formulas
Areas of 2-dimensional figures
- A triangle: (where B is any side, and h is the distance from the line on which B lies to the other vertex of the triangle). This formula can be used if the height h is known. If the lengths of the three sides are known then Heron's formula can be used: where a, b, c are the sides of the triangle, and is half of its perimeter. If an angle and its two included sides are given, the area is where C is the given angle and a and b are its included sides. If the triangle is graphed on a coordinate plane, a matrix can be used and is simplified to the absolute value of . This formula is also known as the shoelace formula and is an easy way to solve for the area of a coordinate triangle by substituting the 3 points (x1,y1), (x2,y2), and (x3,y3). The shoelace formula can also be used to find the areas of other polygons when their vertices are known. Another approach for a coordinate triangle is to use calculus to find the area.
- A simple polygon constructed on a grid of equal-distanced points (i.e., points with integer coordinates) such that all the polygon's vertices are grid points: , where i is the number of grid points inside the polygon and b is the number of boundary points. This result is known as Pick's theorem.
Surface area of 3-dimensional figures
- Cone: , where r is the radius of the circular base, and h is the height. That can also be rewritten as or where r is the radius and l is the slant height of the cone. is the base area while is the lateral surface area of the cone.
- Cube: , where s is the length of an edge.
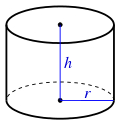
- Cylinder: , where r is the radius of a base and h is the height. The 2r can also be rewritten as d, where d is the diameter.
- Prism: 2B + Ph, where B is the area of a base, P is the perimeter of a base, and h is the height of the prism.
- Pyramid: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B + \frac{PL}{2}} , where B is the area of the base, P is the perimeter of the base, and L is the length of the slant.
- Rectangular prism: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 (\ell w + \ell h + w h)} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell} is the length, w is the width, and h is the height.
General formula for surface area
The general formula for the surface area of the graph of a continuously differentiable function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=f(x,y),} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,y)\in D\subset\mathbb{R}^2} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} is a region in the xy-plane with the smooth boundary:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\iint_D\sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2+1}\,dx\,dy. }
An even more general formula for the area of the graph of a parametric surface in the vector form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\mathbf{r}(u,v),} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}} is a continuously differentiable vector function of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u,v)\in D\subset\mathbb{R}^2} is:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\iint_D \left|\frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\right|\,du\,dv. }
List of formulas
The above calculations show how to find the areas of many common shapes.
The areas of irregular (and thus arbitrary) polygons can be calculated using the "Surveyor's formula" (shoelace formula).
Relation of area to perimeter
The isoperimetric inequality states that, for a closed curve of length L (so the region it encloses has perimeter L) and for area A of the region that it encloses,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\pi A \le L^2,}
and equality holds if and only if the curve is a circle. Thus a circle has the largest area of any closed figure with a given perimeter.
At the other extreme, a figure with given perimeter L could have an arbitrarily small area, as illustrated by a rhombus that is "tipped over" arbitrarily far so that two of its angles are arbitrarily close to 0° and the other two are arbitrarily close to 180°.
For a circle, the ratio of the area to the circumference (the term for the perimeter of a circle) equals half the radius r. This can be seen from the area formula πr2 and the circumference formula 2πr.
The area of a regular polygon is half its perimeter times the apothem (where the apothem is the distance from the center to the nearest point on any side).
Fractals
Doubling the edge lengths of a polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the dimension of the space the polygon resides in). But if the one-dimensional lengths of a fractal drawn in two dimensions are all doubled, the spatial content of the fractal scales by a power of two that is not necessarily an integer. This power is called the fractal dimension of the fractal.
Area bisectors
There are an infinitude of lines that bisect the area of a triangle. Three of them are the medians of the triangle (which connect the sides' midpoints with the opposite vertices), and these are concurrent at the triangle's centroid; indeed, they are the only area bisectors that go through the centroid. Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle.
Any line through the midpoint of a parallelogram bisects the area.
All area bisectors of a circle or other ellipse go through the center, and any chords through the center bisect the area. In the case of a circle they are the diameters of the circle.
Optimization
Given a wire contour, the surface of least area spanning ("filling") it is a minimal surface. Familiar examples include soap bubbles.
The question of the filling area of the Riemannian circle remains open. The circle has the largest area of any two-dimensional object having the same perimeter.
A cyclic polygon (one inscribed in a circle) has the largest area of any polygon with a given number of sides of the same lengths.
A version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral.
The triangle of largest area of all those inscribed in a given circle is equilateral; and the triangle of smallest area of all those circumscribed around a given circle is equilateral.
The ratio of the area of the incircle to the area of an equilateral triangle, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{3\sqrt{3}}} , is larger than that of any non-equilateral triangle.
The ratio of the area to the square of the perimeter of an equilateral triangle, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{12\sqrt{3}},} is larger than that for any other triangle.
Licensing
Content obtained and/or adapted from:
- Perimeter, Wikipedia under a CC BY-SA license
- Area, Wikipedia under a CC BY-SA license


















![{\displaystyle \gamma :[0,2\pi ]\rightarrow \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bea32becc154f483bda6d73f47426b17ddd93952)







![{\displaystyle \gamma :[a,b]\rightarrow \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab36f66326a2b397f9661b314c5be85338c3b8de)