Absolute Value Functions

Introduction

The graph of the absolute value function for real numbers

The graph of the function $y=|5x+5|$

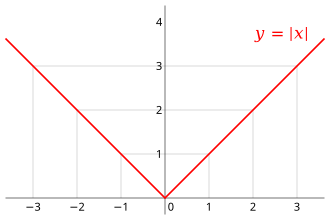
In mathematics, the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x if x is positive, and |x| = −x if x is negative (in which case −x is positive), and |0| = 0. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its "distance from zero". The absolute value function f(x) = |a| can be expressed as a piecewise function, where f(x) = a when a ≥ 0, and f(x) = -a when a < 0. We can use this to help us visualize, graph, or solve other absolute value functions.

Here are some examples of absolute value functions:

• $g(x)=|5x+5|$. 5x + 5 ≥ 0 when x ≥ -1, and 5x + 5 < 0 when x < -1. So, g(x) = 5x + 5 when x ≥ -1, and g(x) = -5x - 5 when x < -1.
• $h(x)=|x^{2}-4|$. $x^{2}-4\geq 0$ when -2 ≥ x or x ≥ 2. So, $h(x)=x^{2}-4$ when -2 ≥ x or x ≥ 2, and $h(x)=-x^{2}+4$ when -2 < x < 2.