Ratio and Root Tests

Ratio Test

In mathematics, the ratio test is a test (or "criterion") for the convergence of a series

$\sum _{n=1}^{\infty }a_{n},$

where each term is a real or complex number and a_n is nonzero when n is large. The test was first published by Jean le Rond d'Alembert and is sometimes known as d'Alembert's ratio test or as the Cauchy ratio test.

The test

Decision diagram for the ratio test

The usual form of the test makes use of the limit

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|.$

The ratio test states that:

• if L < 1 then the series converges absolutely;
• if L > 1 then the series is divergent;
• if L = 1 or the limit fails to exist, then the test is inconclusive, because there exist both convergent and divergent series that satisfy this case.

It is possible to make the ratio test applicable to certain cases where the limit L fails to exist, if limit superior and limit inferior are used. The test criteria can also be refined so that the test is sometimes conclusive even when L = 1. More specifically, let

$R=\lim \sup \left|{\frac {a_{n+1}}{a_{n}}}\right|$

$r=\lim \inf \left|{\frac {a_{n+1}}{a_{n}}}\right|$.

Then the ratio test states that:

• if R < 1, the series converges absolutely;
• if r > 1, the series diverges;
• if $\left|{\frac {a_{n+1}}{a_{n}}}\right|\geq 1$ for all large n (regardless of the value of r), the series also diverges; this is because $|a_{n}|$ is nonzero and increasing and hence a_n does not approach zero;
• the test is otherwise inconclusive.

If the limit L in (1) exists, we must have L = R = r. So the original ratio test is a weaker version of the refined one.

Examples

Convergent because L < 1

Consider the series

$\sum _{n=1}^{\infty }{\frac {n}{e^{n}}}$

Applying the ratio test, one computes the limit

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {\frac {n+1}{e^{n+1}}}{\frac {n}{e^{n}}}}\right|={\frac {1}{e}}<1.$

Since this limit is less than 1, the series converges.

Divergent because L > 1

Consider the series

$\sum _{n=1}^{\infty }{\frac {e^{n}}{n}}.$

Putting this into the ratio test:

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {\frac {e^{n+1}}{n+1}}{\frac {e^{n}}{n}}}\right|=e>1.$

Thus the series diverges.

Inconclusive because L = 1

Consider the three series

$\sum _{n=1}^{\infty }1,$

$\sum _{n=1}^{\infty }{\frac {1}{n^{2}}},$

$\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}.$

The first series (1 + 1 + 1 + 1 + ⋯) diverges, the second one (the one central to the Basel problem) converges absolutely and the third one (the alternating harmonic series) converges conditionally. However, the term-by-term magnitude ratios $\left|{\frac {a_{n+1}}{a_{n}}}\right|$ of the three series are respectively $1,$   ${\frac {n^{2}}{(n+1)^{2}}}$    and   ${\frac {n}{n+1}}$. So, in all three cases, one has that the limit $\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|$ is equal to 1. This illustrates that when L = 1, the series may converge or diverge, and hence the original ratio test is inconclusive. In such cases, more refined tests are required to determine convergence or divergence.

Proof

In this example, the ratio of adjacent terms in the blue sequence converges to L=1/2. We choose r = (L+1)/2 = 3/4. Then the blue sequence is dominated by the red sequence r^k for all n ≥ 2. The red sequence converges, so the blue sequence does as well.

Below is a proof of the validity of the original ratio test.

Suppose that $L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|<1$. We can then show that the series converges absolutely by showing that its terms will eventually become less than those of a certain convergent geometric series. To do this, consider a real number r such that $L<r<1$. This implies that $|a_{n+1}|<r|a_{n}|$ for sufficiently large n; say, for all n greater than N. Hence $|a_{n+i}|<r^{i}|a_{n}|$ for each n > N and i > 0, and so

$\sum _{i=N+1}^{\infty }|a_{i}|=\sum _{i=1}^{\infty }\left|a_{N+i}\right|<\sum _{i=1}^{\infty }r^{i}|a_{N}|=|a_{N}|\sum _{i=1}^{\infty }r^{i}=|a_{N}|{\frac {r}{1-r}}<\infty .$

That is, the series converges absolutely.

On the other hand, if L > 1, then $|a_{n+1}|>|a_{n}|$ for sufficiently large n, so that the limit of the summands is non-zero. Hence the series diverges.

Root Test

In mathematics, the root test is a criterion for the convergence (a convergence test) of an infinite series. It depends on the quantity

$\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},$

where $a_{n}$ are the terms of the series, and states that the series converges absolutely if this quantity is less than one, but diverges if it is greater than one. It is particularly useful in connection with power series.

Root test explanation

Decision diagram for the root test

The root test was developed first by Augustin-Louis Cauchy who published it in his textbook Cours d'analyse (1821). Thus, it is sometimes known as the Cauchy root test or Cauchy's radical test. For a series

$\sum _{n=1}^{\infty }a_{n}.$

the root test uses the number

$C=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},$

where "lim sup" denotes the limit superior, possibly ∞+. Note that if

$\lim _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},$

converges then it equals C and may be used in the root test instead.

The root test states that:

• if C < 1 then the series converges absolutely,
• if C > 1 then the series diverges,
• if C = 1 and the limit approaches strictly from above then the series diverges,
• otherwise the test is inconclusive (the series may diverge, converge absolutely or converge conditionally).

There are some series for which C = 1 and the series converges, e.g. $\textstyle \sum 1/{n^{2}}$, and there are others for which C = 1 and the series diverges, e.g. $\textstyle \sum 1/n$.

Application to power series

This test can be used with a power series

$f(z)=\sum _{n=0}^{\infty }c_{n}(z-p)^{n}$

where the coefficients c_n, and the center p are complex numbers and the argument z is a complex variable.

The terms of this series would then be given by a_n = c_n(z − p)ⁿ. One then applies the root test to the a_n as above. Note that sometimes a series like this is called a power series "around p", because the radius of convergence is the radius R of the largest interval or disc centred at p such that the series will converge for all points z strictly in the interior (convergence on the boundary of the interval or disc generally has to be checked separately). A corollary of the root test applied to such a power series is the Cauchy–Hadamard theorem: the radius of convergence is exactly $1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}},$ taking care that we really mean ∞ if the denominator is 0.

Proof

The proof of the convergence of a series Σa_n is an application of the comparison test. If for all n ≥ N (N some fixed natural number) we have ${\sqrt[{n}]{|a_{n}|}}\leq k<1,$ then $|a_{n}|\leq k^{n}<1$. Since the geometric series $\sum _{n=N}^{\infty }k^{n}$ converges so does $\sum _{n=N}^{\infty }|a_{n}|$ by the comparison test. Hence Σa_n converges absolutely.

If ${\sqrt[{n}]{|a_{n}|}}>1$ for infinitely many n, then a_n fails to converge to 0, hence the series is divergent.

Proof of corollary: For a power series Σa_n = Σc_n(z − p)ⁿ, we see by the above that the series converges if there exists an N such that for all n ≥ N we have

${\sqrt[{n}]{|a_{n}|}}={\sqrt[{n}]{|c_{n}(z-p)^{n}|}}<1,$

equivalent to

${\sqrt[{n}]{|c_{n}|}}\cdot |z-p|<1$

for all n ≥ N, which implies that in order for the series to converge we must have $|z-p|<1/{\sqrt[{n}]{|c_{n}|}}$ for all sufficiently large n. This is equivalent to saying

$|z-p|<1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}},$

so $R\leq 1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}.$ Now the only other place where convergence is possible is when

${\sqrt[{n}]{|a_{n}|}}={\sqrt[{n}]{|c_{n}(z-p)^{n}|}}=1,$

(since points > 1 will diverge) and this will not change the radius of convergence since these are just the points lying on the boundary of the interval or disc, so

$R=1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}.$

Examples

Example 1:

$\sum _{i=1}^{\infty }{\frac {2^{i}}{i^{9}}}$

Applying the root test and using the fact that $\lim _{n\rightarrow \infty }n^{1/n}=1,$

$C={\sqrt[{n}]{|{\frac {2^{n}}{n^{9}}}|}}={\frac {\sqrt[{n}]{2^{n}}}{\sqrt[{n}]{n^{9}}}}={\frac {2}{(n^{1/n})^{9}}}=2$

Since $C=2>1,$ the series diverges.

Example 2:

$1+1+0.5+0.5+0.25+0.25+0.125+0.125+...$

The root test shows convergence because

$r=\limsup _{n\to \infty }{\sqrt[{n}]{|a_{n}|}}=\limsup _{n\to \infty }{\sqrt[{n}]{|.5^{n}|}}=.5<1.$

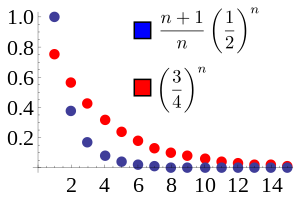
This example shows how the root test is stronger than the ratio test. The ratio test is inconclusive for this series if $n$ is odd so $a_{n}=a_{n+1}=.5^{n}$ (though not if $n$ is even), because

$r=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {2\cdot .5^{n}}{2\cdot .5^{n}}}\right|=1.$

Resources

The Ratio Test

• The Ratio Test Video by James Sousa, Math is Power 4U
• The Ratio Test I Video by James Sousa, Math is Power 4U
• The Ratio Test II Video by James Sousa, Math is Power 4U
• Ex 1: The Ratio Test Video by James Sousa, Math is Power 4U
• Ex 2: The Ratio Test Video by James Sousa, Math is Power 4U
• Ex 3: The Ratio Test Video by James Sousa, Math is Power 4U
• Ex 4: The Ratio Test Video by James Sousa, Math is Power 4U

• Using the Ratio Test to Determine if a Series Converges #1 Video by Patrick JMT
• Using the Ratio Test to Determine if a Series Converges #2 Video by Patrick JMT
• Using the Ratio Test to Determine if a Series Converges #3 Video by Patrick JMT
• The Ratio Test - Another Example #1 Video by Patrick JMT
• The Ratio Test - Another Example #2 Video by Patrick JMT
• The Ratio Test - Another Example #3 Video by Patrick JMT
• The Ratio Test - Another Example #4 Video by Patrick JMT

• The Ratio Test Video by Krista King
• The Ratio Test with Factorials Video by Krista King

• The Ratio Test Video by The Organic Chemistry Tutor

The Root Test

• The Root Test Video by Math is Power 4U
• The Root Test I Video by Math is Power 4U
• The Root Test II Video by Math is Power 4U
• Ex 1 The Root Test Video by Math is Power 4U
• Ex 2 The Root Test Video by Math is Power 4U
• Ex 3 The Root Test Video by Math is Power 4U
• Ex 4 The Root Test Video by Math is Power 4U
• Ex 5 The Root Test Video by Math is Power 4U

• The Root Test for Series Video by Patrick JMT
• The Root Test Another Example 1 Video by Patrick JMT
• The Root Test Another Example 2 Video by Patrick JMT
• The Root Test Another Example 3 Video by Patrick JMT

• The Root Test Video by Krista King

• The Root Test Video by The Organic Chemistry Tutor

References

1. Rudin, Walter (1976), Principles of Mathematical Analysis (3rd ed.), New York: McGraw-Hill, Inc., ISBN 978-0-07-054235-8: §3.34.
2. Apostol, Tom M. (1974), Mathematical analysis (2nd ed.), Addison-Wesley, ISBN 978-0-201-00288-1: §8.14.
3. Bottazzini, Umberto (1986), The Higher Calculus: A History of Real and Complex Analysis from Euler to Weierstrass, Springer-Verlag, pp. 116–117, ISBN 978-0-387-96302-0. Translated from the Italian by Warren Van Egmond
4. Briggs, William; Cochrane, Lyle (2011). Calculus: Early Transcendentals. Addison Wesley. p. 571.
5. Knopp, Konrad (1956). "§ 3.2". Infinite Sequences and Series. Dover publications, Inc., New York. ISBN 0-486-60153-6.
6. Whittaker, E. T. & Watson, G. N. (1963). "§ 2.35". A Course in Modern Analysis (fourth ed.). Cambridge University Press. ISBN 0-521-58807-3.