Defining the Derivative
Contents
The Definition of Slope
Historically, the primary motivation for the study of differentiation was the tangent line problem: for a given curve, find the slope of the straight line that is tangent to the curve at a given point. The word tangent comes from the Latin word tangens, which means touching. Thus, to solve the tangent line problem, we need to find the slope of a line that is "touching" a given curve at a given point, or, in modern language, that has the same slope. But what exactly do we mean by "slope" for a curve?
The solution is obvious in some cases: for example, a line is its own tangent; the slope at any point is . For the parabola , the slope at the point is ; the tangent line is horizontal.
But how can you find the slope of, say, at ? This is in general a nontrivial question, but first we will deal carefully with the slope of lines.
The Slope of a Line
The slope of a line, also called the gradient of the line, is a measure of its inclination. A line that is horizontal has slope 0, a line from the bottom left to the top right has a positive slope and a line from the top left to the bottom right has a negative slope.
The slope can be defined in two (equivalent) ways. The first way is to express it as how much the line climbs for a given motion horizontally. We denote a change in a quantity using the symbol (pronounced "delta"). Thus, a change in is written as . We can therefore write this definition of slope as:
An example may make this definition clearer. If we have two points on a line, and , the change in from to is given by:
Likewise, the change in from to is given by:
This leads to the very important result below.
- The slope of the line between the points and is
Alternatively, we can define slope trigonometrically , using the tangent function:
where is the angle from the rightward-pointing horizontal to the line, measured counter-clockwise. If you recall that the tangent of an angle is the ratio of the y-coordinate to the x-coordinate on the unit circle, you should be able to spot the equivalence here.
Of a graph of a function
The graphs of most functions we are interested in are not straight lines (although they can be), but rather curves. We cannot define the slope of a curve in the same way as we can for a line. In order for us to understand how to find the slope of a curve at a point, we will first have to cover the idea of tangency. Intuitively, a tangent is a line which just touches a curve at a point, such that the angle between them at that point is 0. Consider the following four curves and lines:
| (i) | (ii) |

|

|
| (iii) | (iv) |

|

|
- The line crosses, but is not tangent to at .
- The line crosses, and is tangent to at .
- The line crosses at two points, but is tangent to only at .
- There are many lines that cross at , but none are tangent. In fact, this curve has no tangent at .
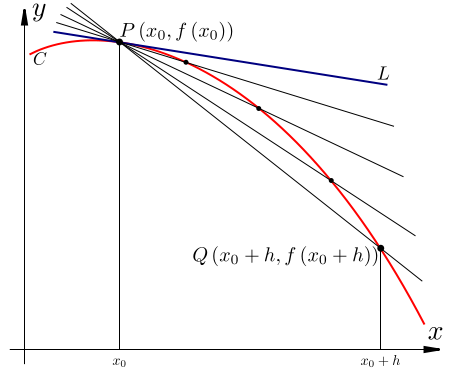
A secant is a line drawn through two points on a curve. We can construct a definition of a tangent as the limit of a secant of the curve taken as the separation between the points tends to zero. Consider the diagram below.
As the distance tends to 0, the secant line becomes the tangent at the point . The two points we draw our line through are:
and
As a secant line is simply a line and we know two points on it, we can find its slope, , using the formula from before:
(We will refer to the slope as because it may, and generally will, depend on .) Substituting in the points on the line,
This simplifies to
This expression is called the difference quotient. Note that can be positive or negative — it is perfectly valid to take a secant through any two points on the curve — but cannot be .
The definition of the tangent line we gave was not rigorous, since we've only defined limits of numbers — or, more precisely, of functions that output numbers — not of lines. But we can define the slope of the tangent line at a point rigorously, by taking the limit of the slopes of the secant lines from the last paragraph. Having done so, we can then define the tangent line as well. Note that we cannot simply set to 0 as this would imply division of 0 by 0 which would yield an undefined result. Instead we must find the limit of the above expression as tends to 0:
Definition: Slope of the graph of a function
- The slope of the graph of at the point is
If this limit does not exist, then we say the slope is undefined.
If the slope is defined, say , then the tangent line to the graph of at the point is the line with equation
This last equation is just the point-slope form for the line through with slope .
The Definition of the Derivative
You may have noticed that the two operations we've discussed — computing the slope of the tangent to the graph of a function and computing the instantaneous rate of change of the function — involved exactly the same limit. That is, the slope of the tangent to the graph of is . Of course, can, and generally will, depend on , so we should really think of it as a function of . We call this process (of computing ) differentiation. Differentiation results in another function whose value for any value is the slope of the original function at . This function is known as the derivative of the original function.
Since lots of different sorts of people use derivatives, there are lots of different mathematical notations for them. Here are some:
- (read "f prime of x") for the derivative of ,
- ,
- ,
- for the derivative of as a function of or
- , which is more useful in some cases.
Most of the time the brackets are not needed, but are useful for clarity if we are dealing with something like , where we want to differentiate the product of two functions, and .
The first notation has the advantage that it makes clear that the derivative is a function. That is, if we want to talk about the derivative of at , we can just write .
In any event, here is the formal definition:
Definition: (derivative)
- Let be a function. Then wherever this limit exists. In this case we say that is differentiable at and its derivative at is .
Examples
Example 1
The derivative of is
no matter what is. This is consistent with the definition of the derivative as the slope of a function.
Example 2
What is the slope of the graph of at ? We can do it "the hard (and imprecise) way", without using differentiation, as follows, using a calculator and using small differences below and above the given point:
When , .
When , .
Then the difference between the two values of is .
Then the difference between the two values of is .
Thus, the slope at the point of the graph at which .
But, to solve the problem precisely, we compute
We were lucky this time; the approximation we got above turned out to be exactly right. But this won't always be so, and, anyway, this way we didn't need a calculator.
In general, the derivative of is
Example 3
If (the absolute value function) then , which can also be stated as
Finding this derivative is a bit complicated, so we won't prove it at this point.
Here, is not smooth (though it is continuous) at and so the limits and (the limits as 0 is approached from the right and left respectively) are not equal. From the definition, , which does not exist. Thus, is undefined, and so has a discontinuity at 0. This sort of point of non-differentiability is called a cusp. Functions may also not be differentiable because they go to infinity at a point, or oscillate infinitely frequently.
Understanding the derivative notation
The derivative notation is special and unique in mathematics. The most common notation for derivatives you'll run into when first starting out with differentiating is the Leibniz notation, expressed as . You may think of this as "rate of change in with respect to " . You may also think of it as "infinitesimal value of divided by infinitesimal value of " . Either way is a good way of thinking, although you should remember that the precise definition is the one we gave above. Often, in an equation, you will see just , which literally means "derivative with respect to x". This means we should take the derivative of whatever is written to the right; that is, means where .
As you advance through your studies, you will see that we sometimes pretend that and are separate entities that can be multiplied and divided, by writing things like . Eventually you will see derivatives such as , which just means that the input variable of our function is called and our output variable is called ; sometimes, we will write , to mean the derivative with respect to of whatever is written on the right. In general, the variables could be anything, say .
All of the following are equivalent for expressing the derivative of
Tangent Lines
Since we can find the gradient of a function at any point we can also find the equation of the tangent line to the function at any point:
What is the equation of the tangent line for the curve at the point x = -4?
First we need to find the derivative of the equation.
Then we find the gradient at the point x = -4.
Using the original function we find the corresponding y value to the x value at the point of tangency.
Then we use the point-gradient equation to find the equation.
so the equation of the tangent line is y = -5x - 32....
Resources
- Defining the Derivative PowerPoint file created by Dr. Sara Shirinkam, UTSA.
- Understanding the Definition of the Derivative by patrickJMT
- Definition of the Derivative by The Organic Chemistry Tutor
- Calculus 1 - Derivatives by The Organic Chemistry Tutor
Licensing
Content obtained and/or adapted from:
- Differentiation, Wikibooks: A-level Mathematics/OCR/C1 under a CC BY-SA license
- Differentiation Defined, Wikibooks: Calculus/Differentiation under a CC BY-SA license




































![{\displaystyle \lim _{h\to 0}\left[{\frac {f(x_{0}+h)-f(x_{0})}{h}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d4bd8965a03018d783a87573829f2113ec86fb4)




![{\displaystyle D_{x}[f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0bc0c64c0455d3e24668b95c4790e57806572f3)

![{\displaystyle {\frac {d}{dx}}{\big [}y{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a51a0607b2d4e9448055729d46246c4c9dc429)



























































