Vectors in The Plane, Space

From Department of Mathematics at UTSA
Revision as of 10:02, 2 November 2021 by Lila (talk | contribs) (→‎Resources)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Jump to navigation Jump to search

See also: Vectors

"Higher-dimensional geometry" sounds exotic. It is exotic— interesting and eye-opening. But it isn't distant or unreachable.

We begin by defining one-dimensional space to be the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^1 } . To see that definition is reasonable, draw a one-dimensional space

Linalg line.png

and make the usual correspondence with : pick a point to label Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} and another to label Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} .

Linalg line with unit.png

Now, with a scale and a direction, finding the point corresponding to, say Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +2.17 } , is easy— start at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 } and head in the direction of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 } (i.e., the positive direction), but don't stop there, go Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.17 } times as far.

The basic idea here, combining magnitude with direction, is the key to extending to higher dimensions.

An object comprised of a magnitude and a direction is a vector (we will use the same word as in the previous section because we shall show below how to describe such an object with a column vector). We can draw a vector as having some length, and pointing somewhere.

Linalg vectors 1.png

There is a subtlety here— these vectors

Linalg vectors 2.png

are equal, even though they start in different places, because they have equal lengths and equal directions. Again: those vectors are not just alike, they are equal.

How can things that are in different places be equal? Think of a vector as representing a displacement ("vector" is Latin for "carrier" or "traveler"). These squares undergo the same displacement, despite that those displacements start in different places.

Linalg vectors 3.png

Free Vectors

Sometimes, to emphasize this property vectors have of not being anchored, they are referred to as free vectors. Thus, these free vectors are equal as each is a displacement of one over and two up.

Linalg vectors 4.png

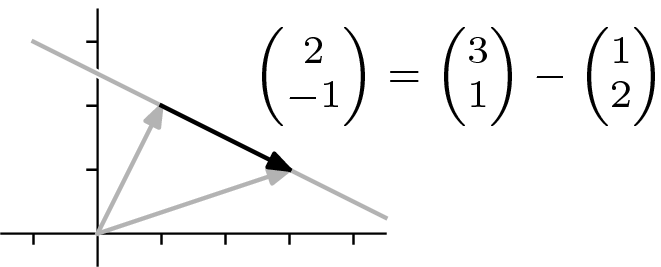
More generally, vectors in the plane are the same if and only if they have the same change in first components and the same change in second components: the vector extending from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_1,a_2) } to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (b_1,b_2) } equals the vector from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (c_1,c_2) } to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (d_1,d_2) } if and only if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1-a_1=d_1-c_1 } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2-a_2=d_2-c_2 } .

An expression like "the vector that, were it to start at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_1,a_2) } , would extend to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (b_1,b_2) } " is awkward. We instead describe such a vector as

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} b_1-a_1 \\ b_2-a_2 \end{pmatrix} }

so that, for instance, the "one over and two up" arrows shown above picture this vector.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 \\ 2 \end{pmatrix} }

Canonical Position

We often draw the arrow as starting at the origin, and we then say it is in the canonical position (or natural position). When the vector

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} b_1-a_1 \\ b_2-a_2 \end{pmatrix} }

is in its canonical position then it extends to the endpoint Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (b_1-a_1,b_2-a_2)} .

We typically just refer to "the point

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 \\ 2 \end{pmatrix} } "

rather than "the endpoint of the canonical position of" that vector.

Thus, we will call both of these sets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^2 } .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{(x_1,x_2)\,\big|\, x_1,x_2\in\mathbb{R}\} \qquad \{\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\,\big|\, x_1,x_2\in\mathbb{R}\} }

Vector Operations

In the prior section we defined vectors and vector operations with an algebraic motivation;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\cdot\begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \begin{pmatrix} rv_1 \\ rv_2 \end{pmatrix} \qquad \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} + \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} = \begin{pmatrix} v_1+w_1 \\ v_2+w_2 \end{pmatrix} }

we can now interpret those operations geometrically. For instance, if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v} } represents a displacement then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\vec{v}\, } represents a displacement in the same direction but three times as far, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1\vec{v}\, } represents a displacement of the same distance as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}\, } but in the opposite direction.

Linalg scaled vectors.png

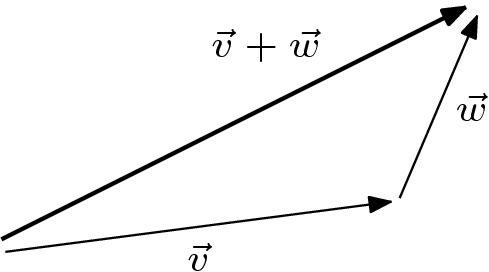
And, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v} } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{w} } represent displacements, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}+\vec{w} } represents those displacements combined.

Linalg vector addition.png

The long arrow is the combined displacement in this sense: if, in one minute, a ship's motion gives it the displacement relative to the earth of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}} and a passenger's motion gives a displacement relative to the ship's deck of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{w}} , then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}+\vec{w}} is the displacement of the passenger relative to the earth.

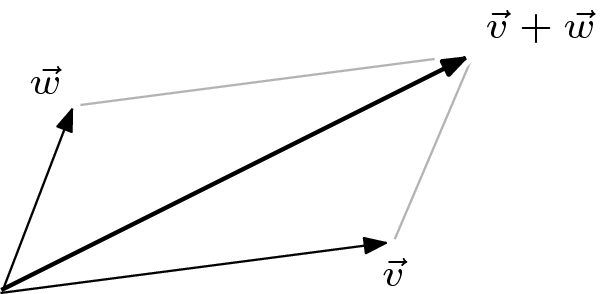
Parallelogram Rule

Another way to understand the vector sum is with the parallelogram rule. Draw the parallelogram formed by the vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}_1,\vec{v}_2} and then the sum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}_1+\vec{v}_2} extends along the diagonal to the far corner.

Linalg vector addition 2.png

The above drawings show how vectors and vector operations behave in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^2 } . We can extend to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^3} , or to even higher-dimensional spaces where we have no pictures, with the obvious generalization: the free vector that, if it starts at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_1,\ldots,a_n) } , ends at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (b_1,\ldots,b_n) } , is represented by this column

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} b_1-a_1 \\ \vdots \\ b_n-a_n \end{pmatrix} }

(vectors are equal if they have the same representation), we aren't too careful to distinguish between a point and the vector whose canonical representation ends at that point,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n= \{\begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix}\,\big|\, v_1,\ldots,v_n\in\mathbb{R}\} }

and addition and scalar multiplication are component-wise.

Having considered points, we now turn to the lines.

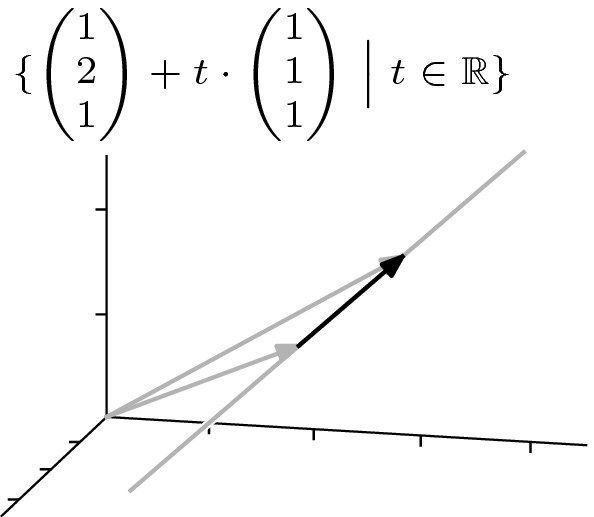
In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^2} , the line through Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,2) } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,1) } s comprised of (the endpoints of) the vectors in this set

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \begin{pmatrix} 1 \\ 2 \end{pmatrix}+t\cdot\begin{pmatrix} 2 \\ -1 \end{pmatrix}\,\big|\, t\in\mathbb{R}\} }

That description expresses this picture.

Linalg vector subtraction.png

Template:AnchorThe vector associated with the parameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} has its whole body in the line— it is a direction vector for the line. Note that points on the line to the left of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=1 } are described using negative values of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t } .

In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^3 } , the line through and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2,3,2) } is the set of (endpoints of) vectors of this form

Linalg line in R3.png

and lines in even higher-dimensional spaces work in the same way.

If a line uses one parameter, so that there is freedom to move back and forth in one dimension, then a plane must involve two. For example, the plane through the points Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,0,5) } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2,1,-3) } , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-2,4,0.5) } consists of (endpoints of) the vectors in

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \begin{pmatrix} 1 \\ 0 \\ 5 \end{pmatrix} +t\cdot\begin{pmatrix} 1 \\ 1 \\ -8 \end{pmatrix} +s\cdot\begin{pmatrix} -3 \\ 4 \\ -4.5 \end{pmatrix} \,\big|\, t,s\in\mathbb{R} \} }

(the column vectors associated with the parameters

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 \\ 1 \\ -8 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix} - \begin{pmatrix} 1 \\ 0 \\ 5 \end{pmatrix} \qquad \begin{pmatrix} -3 \\ 4 \\ -4.5 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 0.5 \end{pmatrix} - \begin{pmatrix} 1 \\ 0 \\ 5 \end{pmatrix} }

are two vectors whose whole bodies lie in the plane). As with the line, note that some points in this plane are described with negative Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} 's or negative Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} 's or both.

A description of planes that is often encountered in algebra and calculus uses a single equation as the condition that describes the relationship among the first, second, and third coordinates of points in a plane.

Linalg plane.png

The translation from such a description to the vector description that we favor in this book is to think of the condition as a one-equation linear system and parametrize Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=(1/2)(4-y-z) } .

Linalg plane with basis.png

Linear Surface

Generalizing from lines and planes, we define a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } -dimensional linear surface (or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } -flat) in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n} to be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\vec{p}+t_1\vec{v}_1+t_2\vec{v}_2+\cdots+t_k\vec{v}_k \,\big|\, t_1,\ldots ,t_k\in\mathbb{R}\}} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}_1,\ldots,\vec{v}_k\in\mathbb{R}^n } . For example, in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^4} ,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\begin{pmatrix} 2 \\ \pi \\ 3 \\ -0.5 \end{pmatrix} +t\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \,\big|\, t\in\mathbb{R}\} }

is a line,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} +t\begin{pmatrix} 1 \\ 1 \\ 0 \\ -1 \end{pmatrix} +s\begin{pmatrix} 2 \\ 0 \\ 1 \\ 0 \end{pmatrix} \,\big|\, t,s\in\mathbb{R}\} }

is a plane, and

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \begin{pmatrix} 3 \\ 1 \\ -2 \\ 0.5 \end{pmatrix} +r\begin{pmatrix} 0 \\ 0 \\ 0 \\ -1 \end{pmatrix} +s\begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \end{pmatrix} +t\begin{pmatrix} 2 \\ 0 \\ 1 \\ 0 \end{pmatrix} \,\big|\, r,s,t\in\mathbb{R}\} }

is a three-dimensional linear surface. Again, the intuition is that a line permits motion in one direction, a plane permits motion in combinations of two directions, etc.

A linear surface description can be misleading about the dimension— this

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=\{ \begin{pmatrix} 1 \\ 0 \\ -1 \\ -2 \end{pmatrix} +t\begin{pmatrix} 1 \\ 1 \\ 0 \\ -1 \end{pmatrix} +s\begin{pmatrix} 2 \\ 2 \\ 0 \\ -2 \end{pmatrix} \,\big|\, t,s\in\mathbb{R}\} }

is a degenerate plane because it is actually a line.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=\{ \begin{pmatrix} 1 \\ 0 \\ -1 \\ -2 \end{pmatrix} +r\begin{pmatrix} 1 \\ 1 \\ 0 \\ -1 \end{pmatrix} \,\big|\, r\in\mathbb{R}\} }

We shall see in the Linear Independence section of Chapter Two what relationships among vectors causes the linear surface they generate to be degenerate.

We finish this subsection by restating our conclusions from the first section in geometric terms. First, the solution set of a linear system with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } unknowns is a linear surface in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n } . Specifically, it is a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } -dimensional linear surface, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } is the number of free variables in an echelon form version of the system. Second, the solution set of a homogeneous linear system is a linear surface passing through the origin. Finally, we can view the general solution set of any linear system as being the solution set of its associated homogeneous system offset from the origin by a vector, namely by any particular solution.

Practice Problems

Vectors in Space (With Solutions)

Resources

Licensing

Content obtained and/or adapted from:

Retrieved from "https://mathresearch.utsa.edu/wiki/index.php?title=Vectors_in_The_Plane,_Space&oldid=3320"