Theorem:Bolzano-Weierstrass

Theorem 1 (Bolzano-Weierstrass): Let $(a_{n})$ be a bounded sequence. Then there exists a subsequence of $(a_{n})$, call it $(a_{n_{k}})$ that is convergent.

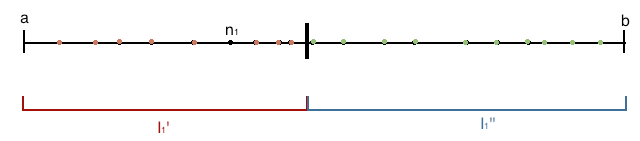
• Proof 1: Let $(a_{n})$ be a bounded sequence, that is the set $\{a_{n}:n\in \mathbb {N} \}$ is bounded. Suppose that $a$ is a lower bound for this set, and $b$ is an upper bound for this set, and so $a\leq a_{n}\leq b_{n}$ for all $n\in \mathbb {N}$. Therefore the set $\{a_{n}:n\in \mathbb {N} \}$ is contained in the interval $I_{1}=[a,b]$.

• Let's take $n_{1}=1$, i.e., let the first term of the subsequence $(a_{n_{k}})$ be equal to the first term of the parent sequence $(a_{n})$.

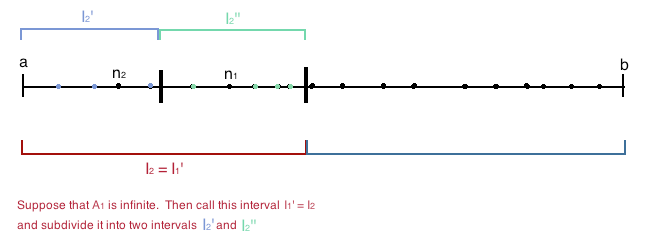
• We will now take the interval $I_{1}$ and divide into two subintervals of equal length. We will call these intervals $I_{1}'$ and $I_{1}''$. We will also divide the set of indices into two sets. Let $A_{1}:=\{n\in \mathbb {N} :n>n_{1},a_{n}\in I_{1}'\}$ and let $B_{1}=\{n\in \mathbb {N} :n>n_{1},a_{N}\in I_{1}''\}$. We note that $A_{1}$ is the set of indices $n$ greater than the first index in our subsequence, $n_{1}$, such that $a_{n}$ is in the interval $I_{1}'$. Similarly, $B_{1}$ is the set of indices $n$ greater than the first index in our subsequence, $n_{1}$ such that $a_{N}$ is in the interval $I_{1}''$.

• We note that both of the sets $A_{1}$ and $B_{1}$ cannot be finite since $A_{1}$ and $B_{1}$ contain all of the indices of the sequence $(a_{n})$ which has infinitely many indices since it is an infinite sequence. If $A_{1}$ is infinite, then we let $I_{2}=I_{1}'$, and we will let $n_{2}$ be the smallest natural number index in the set $A_{1}$, which we are ensured to have by the Well Ordering Principle. If $A_{1}$ is finite, then $B_{1}$ is infinite and we let $I_{2}=I_{1}''$ and we let $n_{2}$ be the smallest natural number index in the set $B_{1}$, which once again, we are ensured to have by the Well Ordering Principle.

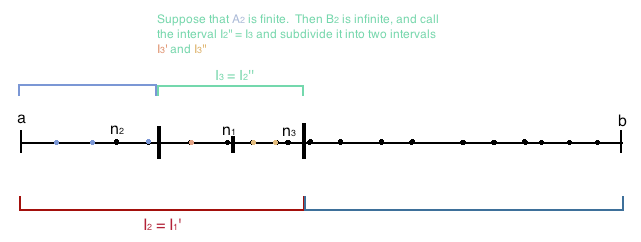
• We will now take the interval $I_{2}$ and subdivide it into two subintervals of equal length, call them $I_{2}'$ and $I_{2}''$. Once again, we will subdivide the set of indices into two sets. Let $A_{2}=\{n\in \mathbb {N} :n>n_{2},a_{n}\in I_{2}'\}$ and let $B_{2}=\{n\in \mathbb {N} :n>n_{2},a_{n}\in I_{2}''\}$.

• Once again, if $A_{2}$ is infinite, then we will let $I_{3}=I_{2}'$, and let $n_{3}$ be the smallest natural number index of $A_{2}$. If $A_{2}$ is finite, then $B_{2}$ is infinite and let $n_{3}$ be the smallest natural number index of $B_{2}$.

• We will then take the interval $I_{3}$ and subdivide it into two subintervals of equal length, call them $I_{3}'$ and $I_{3}''$. We will also subdivide the set of indices into two sets. $A_{3}=\{n\in \mathbb {N} :n>n_{3},a_{n}\in I_{3}'\}$ and $B_{3}=\{n\in \mathbb {N} :n>n_{3},a_{n}\in I_{3}''\}$

• We will continue this pattern to obtain a sequence of nested intervals $I_{1}\supseteq I_{2}\supseteq ...\supseteq I_{k}\supseteq ...$. Furthermore, we will also have a subsequence $(a_{n_{k}})$ of $(a_{n})$ where $a_{n_{k}}\in I_{k}$ for every $k\in \mathbb {N}$.

• We also note that the length of any interval $I_{k}$ is precisely equal to ${\frac {b-a}{2^{k-1}}}$. By the nested intervals theorem there exists a common point $\xi \in I_{k}$ for all $k\in \mathbb {N}$, and so we have that:

${\begin{aligned}\mid a_{n_{k}}-\xi \mid \leq {\frac {b-a}{2^{k-1}}}\end{aligned}}$

• Therefore the subsequence $(a_{n_{k}})$ converges to $\xi$. $\blacksquare$

• Proof 2: Let $(a_{n})$ be a bounded sequence. By the <a href="/the-monotone-subsequence-theorem">The Monotone Subsequence Theorem</a>, every sequence of real numbers has a monotonic subsequence. Let $(a_{n_{k}})$ be this monotonic subsequence. Since $(a_{n})$ is bounded, it follows that $(a_{n_{k}})$ is also bounded since the values $a_{n_{k}}$ are contained in the sequence $(a_{n})$. Since $(a_{n_{k}})$ is both bounded and monotonic, then by <a href="/the-monotone-convergence-theorem">The Monotone Convergence Theorem</a>, $(a_{n_{k}})$ is a convergent subsequence. $\blacksquare$

Theorem 2: If $(a_{n})$ is a bounded sequence such that every convergent subsequence $(a_{n_{k}})$ of $(a_{n})$ converges to $L$ then $(a_{n})$ converges to $L$.

• Proof: Suppose that $A=(a_{n})$ does not converge to $L$. Then there exists a subsequence $A'=(a_{n_{k}})$ and an $\epsilon _{0}>0$ such that $\mid a_{n_{k}}-L\mid \geq \epsilon _{0}$ for all $k\in \mathbb {N}$.

• Since $A$ is bounded, any subsequence of $A$ is also bounded, and so the subsequence $A'$ is bounded. Since $A'$ is bounded, then by the Bolzano-Weierstrass theorem there exists a convergent subsequence $A''$ of $A'$. Since $A''$ is a convergent subsequence of $A'$, then it is also a convergent sequence of $A$ by transitivity, and by the hypothesis, $A''$ converges to $L$.

• But then convergence of $A''$ to $L$ contradicts the assumption that $\mid a_{n_{k}}-L\mid \geq \epsilon _{0}$, and so the assumption that $A$ did not converge to $L$ was false. Therefore $(a_{n})$ converges to $L$. $\blacksquare$

Licensing

Content obtained and/or adapted from:

• The Bolzano-Weierstrass Theorem under a CC BY-SA license