Conics

In mathematics, a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a focus, and some particular line, called a directrix, are in a fixed ratio, called the eccentricity. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the set of points whose coordinates satisfy a quadratic equation in two variables, which may be written in matrix form. This equation allows deducing and expressing algebraically the geometric properties of conic sections.

In the Euclidean plane, the three types of conic sections appear quite different, but share many properties. By extending the Euclidean plane to include a line at infinity, obtaining a projective plane, the apparent difference vanishes: the branches of a hyperbola meet in two points at infinity, making it a single closed curve; and the two ends of a parabola meet to make it a closed curve tangent to the line at infinity. Further extension, by expanding the real coordinates to admit complex coordinates, provides the means to see this unification algebraically.

Standard forms in Cartesian coordinates

Standard forms of an ellipse

Standard forms of a parabola

Standard forms of a hyperbola

After introducing Cartesian coordinates, the focus-directrix property can be used to produce the equations satisfied by the points of the conic section. By means of a change of coordinates (rotation and translation of axes) these equations can be put into standard forms. For ellipses and hyperbolas a standard form has the x-axis as principal axis and the origin (0,0) as center. The vertices are (±a, 0) and the foci (±c, 0). Define b by the equations c² = a² − b² for an ellipse and c² = a² + b² for a hyperbola. For a circle, c = 0 so a² = b². For the parabola, the standard form has the focus on the x-axis at the point (a, 0) and the directrix the line with equation x = −a. In standard form the parabola will always pass through the origin.

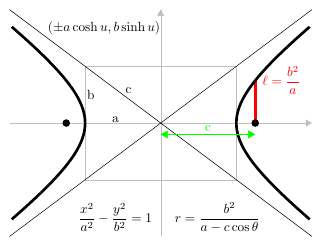
For a rectangular or equilateral hyperbola, one whose asymptotes are perpendicular, there is an alternative standard form in which the asymptotes are the coordinate axes and the line x = y is the principal axis. The foci then have coordinates (c, c) and (−c, −c).

• Circle: $x^{2}+y^{2}=a^{2}$
• Ellipse: ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$
• Parabola: $y^{2}=4ax$ with $a>0$
• Hyperbola: ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$
• Rectangular hyperbola: $xy={\frac {c^{2}}{2}}$

The first four of these forms are symmetric about both the x-axis and y-axis (for the circle, ellipse and hyperbola), or about the x-axis only (for the parabola). The rectangular hyperbola, however, is instead symmetric about the lines {{{1}}} and {{{1}}}.

These standard forms can be written parametrically as,

• Circle: (a cos θ, a sin θ),
• Ellipse: (a cos θ, b sin θ),
• Parabola: (at², 2at),
• Hyperbola: (a sec θ, b tan θ) or (±a cosh u, b sinh u),
• Rectangular hyperbola: $(d\,t,{\frac {d}{t}})$ where $d={\frac {c}{\sqrt {2}}}.$

General Cartesian form

In the Cartesian coordinate system, the graph of a quadratic equation in two variables is always a conic section (though it may be degenerate), and all conic sections arise in this way. The most general equation is of the form

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,$

with all coefficients real numbers and A, B, C not all zero.

Circle

The circle is the simplest and best known conic section. As a conic section, the circle is the intersection of a plane perpendicular to the cone's axis.

The geometric definition of a circle is the locus of all points a constant distance $r$ from a point $(h,k)$ and forming the circumference (C). The distance $r$ is the radius (R) of the circle, and the point $O=(h,k)$ is the circle's center also spelled as centre. The diameter (D) is twice the length of the radius.

Circle illustration with circumference (C) in black, diameter (D) in cyan, radius (R) in red, and centre or origin (O) in magenta.

Equations

Standard Form

The equation for a circle with center $(h,k)$ and radius $r$ is

$(x-h)^{2}+(y-k)^{2}=r^{2}$.

In the simplest case of a circle whose center is at the origin, the equation is simply a restatement of the Pythagorean Theorem:

$x^{2}+y^{2}=r^{2}$

General form

The general form of a circle equation is

$x^{2}+y^{2}+2gx+2fy+c=0$, where

<-g,-f> is the center of the circle.

Polar Coordinates

In the case of a circle centered at the origin, the polar equation of a circle is very simple because polar coordinates are essentially based on circles. For a circle with radius $a$,

$r=a$.

In the more complicated case of a circle with an arbitrary location, the equation is

$r^{2}-2rr_{0}\cos(\theta -\varphi )+r_{0}^{2}=a^{2}$,
where $r_{0}$ is the distance from the circle's center to the origin and $\varphi$ is the angle pointing to the circle.

There are many cases that allow the equation to be simplified. If a point on the circle is touching the origin, its polar equation may consist of a single trig function.

Parametric Equations

When the circle's equation is parametrized with respect to $t$, the equation becomes

$x=h+r\cos t$,
$y=k+r\sin t$.

Ellipse

The geometric definition of an ellipse is the locus of a point which moves in a plane such that the sum of its distances from the two points called foci add up to a constant(greater than the distance between the said foci). Note that a circle is a special case of an ellipse where both foci are at the center of the ellipse, and the major and minor axes are of equal length. An ellipse can also be defined as a conic where the eccentricity is less than one. Ellipses have two directrices, one on each side.

The general equation for an ellipse where its major, or longer, axis is horizontal is : ${\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1$.
Where the major axis is vertical, it is: ${\frac {(y-k)^{2}}{a^{2}}}+{\frac {(x-h)^{2}}{b^{2}}}=1$

• The center is located at $(h,k)$.
• The foci are found at a distance of $c$ from the centre along the major axis, where $c={\sqrt {a^{2}-b^{2}}}$.
• The eccentricity of the ellipse can be found from the formula: $b^{2}=a^{2}(1-e^{2})$ where e is eccentricity. A higher eccentricity makes the curve appear more 'squashed', whereas an eccentricity of 0 makes the ellipse a circle.
• The directrices are the lines $x=\pm {\frac {a}{e}}$
• The major axis has a length of $2a$ and the minor one $2b$.
• The sum of the distance from each point to each of the foci is $2a$.

Parabola

The parabola is another commonly known conic section. The geometric definition of a parabola is the locus of all points such that they are equidistant from a point, known as the focus, and a straight line, called the directrix. In other words the eccentricity of a parabola is equal to 1. The solid formed by rotating a parabola about the axis is called a paraboloid.

Equations

Standard Form

The general form of a vertical parabola is $(x-h)^{2}=4a(y-k)$.

• The axis of the parabola is the line perpendicular to the directrix which passes through the focus, and is the line $x=h$. It is also known as the line of symmetry.
• The vertex is the 'base' of the parabola and is located at $(h,k)$. Therefore, a positive $k$ will move the parabola upwards along its axis $k$ units, while a negative one will move it downwards. This is the same regardless of whether $a$ is a positive or negative number.
• $a$ is the focal length of the parabola. The focus is located at $(h,k+a)$. If $a$ is positive the parabola opens upwards, whereas a negative $a$ causes it to open downwards.
• The directrix is located at $y=k-a$.

If the conic is horizontal, it is the same as a vertical parabola only along the x-axis rather than the y-axis. The general form is: $(y-k)^{2}=4a(x-h)$.

• The axis of the parabola is the line $y=k$.
• The vertex is located at $(h,k)$. A positive $k$ will move the parabola towards the right along its axis $k$ units, while a negative one will move it towards the left. This is the same regardless of whether $a$ is a positive or negative number.
• The focus is located at $(h+a,k)$. If $a$ is positive the parabola opens towards the right, whereas a negative $a$ causes it to open leftwards.
• The directrix is located at $x=h-a$.

Parametric Form

The parametric form of a vertical parabola is:
$x=h+2at$
$y=k+at^{2}$
For a horizontal one:
$x=h+at^{2}$
$y=k+2at$
For both of these forms:

• The vertex is at (h,k)
• The focus is $a$ units from the vertex along the major axis.
• The gradient at any point on the parabola is t, which can be proved by differentiating the parametric form using the chain rule.

Polar Form

The polar form of a parabola is given by $r=-{\frac {2a}{1+cos\theta }}$.

Hyperbolae

A hyperbola can be defined as the locus of all points such that the difference between the distance of each point from two points known as the foci is constant. This is similar to an ellipse, however whereas in an ellipse the distances sum to a constant, here they subtract to one. A hyperbola can also be defined as the locus of all points such that the distance of the point to the closest focus divided by the distance to the directrix, a ratio known as the eccentricity, is a constant greater than one.

Equation

Hyperbola (parameters_a,b,c,h,k)

The general form of a hyperbola with a horizontal transverse axis, i.e. the axis on which the foci lie, is: ${\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1$
A hyperbola with a vertical transverse axis, on the other hand, is of the form: ${\frac {(y-k)^{2}}{a^{2}}}-{\frac {(x-h)^{2}}{b^{2}}}=1$.

• The centre of the hyperbola is $(h,k)$.
• The two foci are found at a distance of $c$ from the centre in each direction along the transverse axis, where $c={\sqrt {a^{2}+b^{2}}}$.
• The eccentricity of the hyperbola can be found by ${\frac {c}{a}}$. A higher eccentricity makes the hyperbola 'steeper', whereas a smaller one makes it more 'curvy'.
• The vertices are a distance of $a$ from the centre of the hyperbola in each direction along the transverse axis.
• The difference between the distances of any point from each of the foci is equal to $2a$.
• Hyperbola also have two asymptotes. An asymptote is a line that points on the graph continuously approach yet never reach. If you extended the graph vast distances along each axis, you would observe it getting closer and closer to the asymptote, however it would never actually reach it. The asymptotes can be found by $y=k\pm {\frac {b}{a}}(x-h)$ for a horizontal hyperbola, or $y=k\pm {\frac {a}{b}}(x-h)$ for a vertical one.

Resources

• Introduction to Conic Sections, Lumen Learning

Licensing

Content obtained and/or adapted from:

• Conic section, Wikipedia under a CC BY-SA license
• Circle, Wikibooks: Conic Sections under a CC BY-SA license
• Ellipse, Wikibooks: Conic Sections under a CC BY-SA license
• Parabola, Wikibooks: Conic Sections under a CC BY-SA license
• Hyperbola, Wikibooks: Conic Sections under a CC BY-SA license