Equations of Lines, Planes and Surfaces in Space

For many practical applications you have to work with the mathematical descriptions of lines, planes, curves, and surfaces in 3-dimensional space. This requires some knowledge on vectors and the ability to construct 3-dimensional graphs without using calculators.

Lines in 3-dimensional space

Although the equation for lines is discussed in previous chapters, this chapter will explain more in detail about the properties and important aspects of lines, as well as the expansion into general curves in 3-dimensional space.

Review of parametric equations

Parametric equations use a different variable to express the relation between two variables. For example, look at the following equation of a circle:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+y^2=1}

If we express variables $x$ and $y$ with a new variable $t$, and we know that $\cos ^{2}t+\sin ^{2}t=1$, we can rewrite the original equation into:

$x=\cos t$

$y=\sin t$

The equation above is the parametric form of a circle with a radius of $1$.

Now, let's talk about lines in 3-dimensional space.

Equations for lines in 3-dimensional space

A line in space is defined by two points in space, which I will call $P_{1}$ and $P_{2}$. Let $\mathbf {r} _{0}$ be the vector from the origin to $P_{1}$, and $\mathbf {r} _{2}$ the vector from the origin to $P_{2}$. Given these two points, every other point $P$ on the line can be reached by

$\mathbf {r} =\mathbf {r} _{0}+\mathbf {v} t$

where $\mathbf {v}$ is the vector from $P_{1}$ and $P_{2}$:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v} = \mathbf{r}_0 - \mathbf{r}_2 }

To intuitively understand the equation of a line, imagine that there is a line going through the end point of the vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_0} and stretches in the direction of the vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} . Just view it as a vector version of the point-slope form. For example, assume there is a line in 3-dimensional space with the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle2,5,4\rangle+\langle1,1,1\rangle t}

We can graph the line by first finding the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2,5,4)} . Then, we stretch the line in the direction parallel with the vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle1,1,1\rangle } . The final graph is the graph of the line Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle2,5,4\rangle+\langle1,1,1\rangle t} . Sometimes the direction vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} is unknown. However, it can be easily solved by finding another point on the line. In this case, the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (5,8,7)} is on the line. By calculating the vector between the two points, we can find out that the direction vector is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle3,3,3\rangle} . Thus, the equation for the line can be written as

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle2,5,4\rangle+\langle3,3,3\rangle t_1}

which is equivalent with the original equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle2,5,4\rangle+\langle1,1,1\rangle t} because if we let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=3t_1} , the original equation will turn into the equation above. Therefore, there are infinitely many ways to write an equation of a line in 3-dimensional space using the vector form. Now, there is a parametric form of expressing a line. Recall that there is another way to write down vectors: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\mathbf{i}+b\mathbf{j}+c\mathbf{k}} . So, we can rewrite the original equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle2,5,4\rangle+\langle1,1,1\rangle t} into:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle2+t,5+t,4+t\rangle=(2+t)\mathbf{i}+(5+t)\mathbf{j}+(4+t)\mathbf{k}}

Then, we assign the respective parts to the corresponding Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,y,z} axes

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=2+t}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=5+t}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=4+t}

This is the parametric form of the equation for lines.

The final common way to notate lines is the symmetric equations, which is just another slight transformation from the parametric form:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x-2=y-5=z-4}

To summarize, there are basically three ways to write the equation for a line that passes through the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,y_0,z_0)} with the direction Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle a,b,c\rangle} .

Vector Equation	Parametric Equations	Symmetric Equations
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle x_0,y_0,z_0\rangle+\langle a,b,c\rangle t}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=x_0+at} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=y_0+bt} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=z_0+ct}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}}

Relations between two lines

There are lines which intersect each other and those which do not. There can be parallel, perpendicular, and skew lines, which will be discussed in this part.

Intersection

Assume there are two lines with the equations:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1:\langle2,5,4\rangle+\langle1,1,1\rangle t} or in parametric form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1: \begin{cases} x=2+t \\ y=5+t \\ z=4+t \end{cases}}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2:\langle5,-1,0\rangle+\langle -\frac{1}{2},4,3\rangle s} or in parametric form $L_{2}:{\begin{cases}x=5-{\frac {1}{2}}s\\y=-1+4s\\z=3s\end{cases}}$

To find out if they intersect or not, we just need to solve the system of equations

${\begin{cases}2+t=5-{\frac {1}{2}}s\\5+t=-1+4s\\4+t=3s\end{cases}}$

If the system of equations has only one solution, then the two lines intersect at one point. If the system of equations has infinitely many solutions, then the two lines are the same. If the system of equations does not have a solution, then the two lines do not intersect at all. In this case, there is a solution:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} t=2 \\ s=2 \end{cases}}

Thus the two lines intersect at point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (4,7,6)} . If we want to further know the angle between the two lines, we can apply the dot product formula. The angle between the two lines should be:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\arccos(\frac{\mathbf{v_1}\,\cdot\,\mathbf{v_2}}{\|\mathbf{v_1}\|\|\mathbf{v_2}\|})}

Parallel

To spot two parallel lines in 3-dimensional space, we just need to look at the direction vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} . If the direction vectors of the two lines Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v_1},\mathbf{v_2}} have such relationship that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v_2}=k\mathbf{v_1}, k\in\mathbb{R}} , then the two lines are parallel with each other. For example, the two lines Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1:\langle2,5,4\rangle+\langle1,1,1\rangle t} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2:\langle5,-1,0\rangle+\langle -3,-3,-3\rangle s} are parallel with each other because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\langle-3,-3,-3\rangle}{-3}=\langle1,1,1\rangle} .

Perpendicular

To have two lines perpendicular with each other, those two lines must intersect first. If they do intersect, recall the dot product of vectors. The dot product states that:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}\,\cdot\,\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta}

If two lines are perpendicular with each other, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\frac{\pi}{2}} , which results in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}\,\cdot\,\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\frac{\pi}{2}=0} .

So, if we continue this flow of thought, we can find that if we choose two vectors on each line, have a dot product between them, and the result is zero, then we can safely say that the two lines are perpendicular with each other. However, there is a more convenient way to simplify the process. Instead of finding two vectors on each line, we just need to apply the dot product on the two direction vectors because the direction vectors are calculated from points on the respective lines.

So if we have two lines:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1:\langle2,5,4\rangle+\langle1,1,1\rangle t} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2:\langle6,6,5\rangle+\langle -2,1,1\rangle s}

They are perpendicular with each other because

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} 2+t=6-2s \\ 5+t=6+s \\ 4+t=5+s \end{cases}} has one and only solution: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} t=2 \\ s=1 \end{cases}} , which means they intersect. And Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle1,1,1\rangle\,\cdot\,\langle-2,1,1\rangle=0}

Thus ending the proof.

Skew lines

Skew lines are lines that do not intersect and are not parallel with each other. For example, lines Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1:\langle2,5,4\rangle+\langle1,1,1\rangle t} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2:\langle5,-1,0\rangle+\langle 3,-3,-3\rangle s} are skew lines.

Distance between two skew lines

To solve this problem, we need to know more about planes in 3-dimensional space, which will be discussed below.

Planes in 3-dimensional space

Introduction

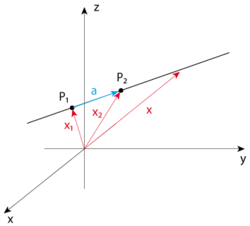
The same idea can be used to describe a plane in 3-dimensional space, which is uniquely defined by three points (which do not lie on a line) in space (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_1, P_2, P_3} ). Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{x}_i} be the vectors from the origin to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_i} . Then

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{x} = \mathbf{x}_1 + \lambda \mathbf{a} + \mu \mathbf{b} }

with:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a} = \mathbf{x}_2 - \mathbf{x}_1 \,\, \text{and} \,\, \mathbf{b} = \mathbf{x}_3 - \mathbf{x}_1 }

Note that the starting point does not have to be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{x}_1 } , but can be any point in the plane. Similarly, the only requirement on the vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a} } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{b} } is that they have to be two non-collinear vectors in our plane.

Recall that in 2-dimensional vectors, if there are two vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{i},\mathbf{j}} , any vector on the Cartesian plane can be expressed in terms of the vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{i},\mathbf{j}} by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\mathbf{i}+b\mathbf{j} \quad (a,b\in\mathbb{R})} . Using the same method, we can deduce that

the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda \mathbf{a} + \mu \mathbf{b}} part tells us that the graph should be a plane, and the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{x} - \mathbf{x}_1} part describes the "slope" and the axes intersections

However, there two other ways to express a plane in 3-dimensional space: the vector equation and the scalar equation.

Vector and scalar equations for planes

The vector equation for planes requires us to understand the power of the dot product. We already knew that when the dot product of two vectors is zero, the two vectors should be perpendicular with each other. Now, imagine a vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}} in 3-dimensional space. If we graph out all the vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\mathbf{r}} that are perpendicular with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}} , what will the result be?

The result should be a plane with a vector perpendicular with the plane. Thus, the vector equation for planes is simply Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}\,\cdot\,\Delta\mathbf{r}=0} .

the vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}} is the normal vector, which is perpendicular with the plane

the vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\mathbf{r}=\mathbf{r}-\mathbf{r_0}} is the variable vector where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle x,y,z \rangle} (unknown points on the plane) and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r_0}=\langle x_0,y_0,z_0 \rangle} (a given point on the plane). This expressions simply means all the vectors on the plane.

Of course, the vector equation for planes can be rewritten as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}\,\cdot\,(\mathbf{r}-\mathbf{r_0})=0} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}\,\cdot\,\mathbf{r}=\mathbf{n}\,\cdot\,\mathbf{r_0}} , depending on the writer.

To find out the scalar equation, we just need to calculate the dot product and do some simplifications. So, let's assume that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}=\langle a,b,c \rangle} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}=\langle x,y,z \rangle} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r_0}=\langle x_0,y_0,z_0 \rangle} According to the vector equation

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}\,\cdot\,(\mathbf{r}-\mathbf{r_0})=0}

Thus, we have

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle a,b,c \rangle\,\cdot\,\langle x-x_0,y-y_0,z-z_0\rangle =0}

After some algebraic manipulations, we can get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax+by+cz-(ax_0+by_0+cz_0)=0}

Since the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax_0+by_0+cz_0} is a constant, we just let $ax_{0}+by_{0}+cz_{0}=-d$. As a result, the scalar equation for planes is $ax+by+cz+d=0$

Note that the constants $a,b,c$ are the same as the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{i},\mathbf{j},\mathbf{k}} components of the normal vector. This property will be extremely useful when discussing the relations between two planes. Also, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -d=\mathbf{n}\,\cdot\,\mathbf{r_0}} .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \blacksquare}

To summarize, there are three ways to notate a plane in 3-dimensional space, with the latter two more commonly used:

Expansion from the equation for lines	Vector equation	Scalar equation
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{x} = \mathbf{x}_1 + \lambda \mathbf{a} + \mu \mathbf{b} }	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}\,\cdot\,(\mathbf{r}-\mathbf{r_0})=0}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax+by+cz+d=0}

Relations between two planes

Parallel

The normal vector is important because it determined the how the plane is shaped. So when we are discussing the relations between two planes, we are actually trying to find out the connections between the normal vectors of the two planes. In this case, assume there are two planes in the 3-dimensional space: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1x+b_1y+c_1z+d_1=0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2x+b_2y+c_2z+d_2=0} . The normal vectors for the planes should be:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n_1}=\langle a_1,b_1,c_1 \rangle,\,\mathbf{n_2}=\langle a_2,b_2,c_2 \rangle}

Since normal vectors are perpendicular with their corresponding planes, if the normal vectors are parallel with each other, the respective planes should also be parallel with each other. Thus,

If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n_1}=k\mathbf{n_2}\quad(k\in\mathbb{R})} , then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1x+b_1y+c_1z+d_1=0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2x+b_2y+c_2z+d_2=0} are parallel with each other.

Perpendicular

If the normal vectors are perpendicular with each other, the respective planes will be perpendicular. In other words, if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n_1}\perp\mathbf{n_2}} , then the planes are perpendicular with each other.

Intersection

To fully understand how to find the intersection between two lines, we should be familiar with the normal vector and its potential. If the two planes are not parallel and are not basically the same plane, then they must intersect with each other. The intersection should form a line. Imagine there are two planes Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1x+b_1y+c_1z+d_1=0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2x+b_2y+c_2z+d_2=0} , and their respective normal vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n_1}\ne k\mathbf{n_2}\quad(k\in\mathbb{R})} (which means they are not parallel).

Because normal vectors are perfectly perpendicular to all vectors on the plane, the opposite is also true: all vectors on the plane are perpendicular to their respective normal vectors. This is why Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}\,\cdot\,(\mathbf{r}-\mathbf{r_0})=0} is the vector equation of the plane. Since the intersection of the two planes is a line, we can say that the direction vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} should be on both planes.

Because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} is on both planes, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} should be perpendicular with both normal vectors

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}\perp\mathbf{n_1},\,\mathbf{v}\perp\mathbf{n_2}}

Recall that the cross product of two vectors will result in a new vector that is perpendicular with both the original vectors. We can calculate the cross product of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n_1}, \mathbf{n_2}} to create Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}} .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n_1}\times\mathbf{n_2}= \begin{vmatrix} \mathbf{i}&\mathbf{j}&\mathbf{k}\\ a_1&b_1&c_1\\ a_2&b_2&c_2 \end{vmatrix}= (b_1c_2-b_2c_1)\mathbf{i}-(a_1c_2-a_2c_1)\mathbf{j}+(a_1b_2-a_2b_1)\mathbf{k}}

So the direction vector for the line is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}=\mathbf{n_1}\times\mathbf{n_2}=\langle b_1c_2-b_2c_1,a_1c_2-a_2c_1,a_1b_2-a_2b_1\rangle}

We still need to know a point on the line to finish the equation because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r} = \mathbf{r}_0 + \mathbf{v}t } . To find a point, simply let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=0 } and solve for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,y } in the following system of equations

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} a_1x+b_1y+d_1=0 \\ a_2x+b_2y+d_2=0 \end{cases}\Rightarrow \begin{cases} x=\frac{b_1d_2-b_2d_1}{a_1b_2-a_2b_1} \\ y=\frac{a_1d_2-a_2d_1}{a_2b_1-a_1b_2} \end{cases} }

Because the solution is too complicated to write down, we will let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{b_1d_2-b_2d_1}{a_1b_2-a_2b_1}=x_0 } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\frac{a_1d_2-a_2d_1}{a_2b_1-a_1b_2}=y_0 } . Thus, the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,y_0,0) } is on both planes (recall that we let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=0 } ) and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{P_0}=\langle x_0,y_0,0 \rangle } .

Now, we know a point on the line Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,y_0,0) } and the direction vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v}=\mathbf{n_1}\times\mathbf{n_2}=\langle b_1c_2-b_2c_1,a_1c_2-a_2c_1,a_1b_2-a_2b_1\rangle} , the intersection between the two planes is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L:\langle \frac{b_1d_2-b_2d_1}{a_1b_2-a_2b_1},\frac{a_1d_2-a_2d_1}{a_2b_1-a_1b_2},0 \rangle+\langle b_1c_2-b_2c_1,a_1c_2-a_2c_1,a_1b_2-a_2b_1\rangle t }

For those who prefer a cleaner expression:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L:\langle x_0,y_0,0 \rangle+\langle b_1c_2-b_2c_1,a_1c_2-a_2c_1,a_1b_2-a_2b_1\rangle t }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L:\mathbf{P_0}+(\mathbf{n_1}\times\mathbf{n_2})t }

And if we want to know the angle between the planes, similar to how we find out the angle between two lines, we apply the dot product:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\arccos(\frac{\mathbf{n_1}\,\cdot\,\mathbf{n_2}}{\|\mathbf{n_1}\|\|\mathbf{n_2}\|}) }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \blacksquare }

Distance between two parallel planes

The distance between two non-parallel planes is zero because they intersect. So, we should focus on the distance between parallel planes. Before we do that, it will be more convenient if we know the distance from a point to a plane.

Let the distance be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} , the point be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P=(x_1,y_1,z_1)} , the plane be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax+by+cz+d=0} .

Knowing the equation for the plane can help us know the normal vector, since the normal vector is perpendicular to the plane, the exact direction we need. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}=\langle a,b,c \rangle} .

Now, we start solving. First, assume there is point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_0=(x_0,y_0,z_0)} on the plane Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax+by+cz+d=0} . Then, we create a vector from $P_{0}$ to $P$: ${\overrightarrow {P_{0}P}}=\langle x_{1}-x_{0},y_{1}-y_{0},z_{1}-z_{0}\rangle$. We will also let the angle between vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{P_0 P}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}} be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} . If we graph out what it looks like, we can easily understand how the distance is deduced.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D= | \|\overrightarrow{P_0 P}\|\ \cos\theta |} (the absolute value is needed because the distance should always be larger than zero)

However, we do not know Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} . We can calculate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} by applying the dot product. But, there is a simpler way:

Using some very interesting manipulation, we can get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\frac{|\|\mathbf{n}\|\|\overrightarrow{P_0 P}\|\cos\theta|}{\|\mathbf{n}\|}}

As we can see, the nominator is actually the other way of expressing the dot product of two vectors. So, we can stop worrying about not knowing the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\frac{|\mathbf{n}\ \cdot\ \overrightarrow{P_0 P}|}{\|\mathbf{n}\|}}

We can now substitute those vectors with their coordinates. After some algebra, we get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\frac{|\mathbf{n}\ \cdot\ \overrightarrow{P_0 P}|}{\|\mathbf{n}\|} =\frac{|ax_1+by_1+cz_1-(ax_0+by_0+cz_0)|}{\sqrt{a^2+b^2+c^2}}}

Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_0=(x_0,y_0,z_0)} is on the plane, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax_0+by_0+cz_0=-d} . We can further simplify the formula into Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\frac{|ax_1+by_1+cz_1+d|}{\sqrt{a^2+b^2+c^2}}} , thus finishing our deduction.

There are other ways to write down the formula. For people who prefer simpler notations, the following formulae are also ways to express the distance:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\frac{|\mathbf{n}\ \cdot\ \overrightarrow{P_0 P}|}{\|\mathbf{n}\|}} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\mathrm{comp}_\mathbf{n} \overrightarrow{P_0 P}}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \blacksquare}

After we do some further "investigation" on the distance formula, we can find that only the equation of the plane and one point are needed to calculate the distance between them, which is very convenient because the fewer things we need to solve a problem, the more convenient the problem is. When we try to find the distance between two parallel planes, we just need one point on one plane and the equation for the other plane to solve.

Distance between two skew lines (continue)

Assume that lines Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1,L_2} are skew lines, we can calculate the distance by assuming that those lines belong in two parallel planes Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_1,P_2 } respectively. Then, the problem changes from solving the distance between two skew lines to solving the distance between two parallel planes.

We still need to know the normal vector of both planes. We can simply apply the cross product on the two direction vectors of both lines: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}=\mathbf{v_1}\times\mathbf{v_2}} . Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}\ne0} because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v_1},\mathbf{v_2}} are not pointing towards the same direction. Now we can apply the newly deduced distance formula on the two skew lines.

Cylinders and quadric surfaces

This section of the chapter requires some understanding of conic sections.

Cylinders

An example of a parabolic cylinder in 3-dimensional space

A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. There are several special cylinders such as the parabolic cylinder and the circular cylinder. For example, the image on the right is a parabolic cylinder. Parabolic cylinder typically has an equation of:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x^2} etc.

If we want to move the cylinder around without rotating it, we can have the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z-k=(x-h)^2} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h,k} are constants.

It is just like the parabola we have discussed early but with a new dimension. Circular cylinders, similar to how we derive the parabolic cylinder, looks just like a cylinder with a circle as its "base", with an equation of:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+y^2=1} etc.

If we want to make the circular cylinder more "elliptic", just like how we derive the equation for an ellipse, the elliptic cylinder has an equation of:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,b} are constants.

It is just like an ellipse on the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy} -plane but infinitely stretched in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} direction.

Quadric surfaces

General equation for quadric surfaces: The general equation for quadric surfaces is:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax^2+By^2+Cz^2+Dxy+Eyz+Fxz+Gx+Hy+Iz+J=0}

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B,C,D,E,F,G,H,I,J} are constants.}} It looks similar to the general equation for conic sections (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax^2+Bxy+Cy^2+Dx+Ey+F=0} ), except it has one more variable Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} . After some translations and rotations, we can simplify the general equation into the standard equations:

The standard equations for quadric surfaces are:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax^2+By^2+Cz^2+J=0\quad\text{or}\quad Ax^2+By^2+Iz=0}

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B,C,I,J} are constants.}} Of course, depending on the specific quadric surface, there are different forms of standard equations, which we will see in the following discussions.

Ellipsoid

An ellipsoid with an equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+\frac{y^2}{2}+\frac{z^2}{3}=1} . See that if we intersect the ellipsoid with planes parallel to axis planes, the intersection will always be an ellipse.

Ellipsoids have the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1}

It is difficult to sketch quadric surfaces because instead of two variables, there are three, making the process very complicated without the help of calculators. However, there is a way to make us easier to understand. We can analyze each plane to see what the shape looks like, and then combine what we analyzed from each plane to form a rather complete graph of the surface. Take this for example:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+\frac{y^2}{9}+\frac{z^2}{4}=1}

Let us first examine the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy} -plane. To examine the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy} -plane, we need to imagine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} as a constant. In this case, imagine that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=k} , so

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+\frac{y^2}{9}=1-\frac{k^2}{4}} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2\leq k\leq2} .

We can see that in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy} -plane, the graph will be like an ellipse. We call that the horizontal trace in the plane Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=k} is an ellipse.

Let us furthermore analyze the vertical traces in the planes $x=k,y=k$.

An elliptic paraboloid with equation $z=x^{2}+y^{2}$. Note that the horizontal trace is an ellipse and both vertical traces are parabolas.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{y^2}{9}+\frac{z^2}{4}=1-k^2\quad x=k} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1\leq k\leq 1} .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+\frac{z^2}{4}=1-\frac{k^2}{9}\quad y=k} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -3\leq k\leq3} .

We can see that on both vertical traces in the planes Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=k,y=k} are ellipses. In other words, the graphs in both Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xz} -plane and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle yz} -plane look like ellipses. Since all traces are ellipses, the surface is an ellipsoid with vertices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\pm1,0,0),(0,\pm3,0),(0,0,\pm2)} .

Elliptic paraboloid

Elliptic paraboloids have the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{c}=\frac{x^2}{a^2}+\frac{y^2}{b^2}}

A hyperbolic paraboloid with equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x^2-y^2}

There are variations of the equation depending on which trace is an ellipse. For the equation above, the horizontal trace is an ellipse as seen in the image on the right.

Take Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x^2+y^2} for example. the horizontal trace, which means Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=k} , is:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+y^2=k} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k>0} .

For both vertical traces, we can see that those traces have the shape of a parabola.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x^2+k^2\quad y=k}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=y^2+k^2\quad x=k}

The vertex for this elliptic paraboloid is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0,0)} .

Hyperbolic paraboloid

Hyperbolic paraboloids have the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{c}=\frac{x^2}{a^2}-\frac{y^2}{b^2}}

An image of a cone. Note that vertical traces in the planes Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=k} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=k} are hyperbolas if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\ne0} but are pairs of lines if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=0} .

The respective traces are

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=\frac{k}{c}\quad z=k} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=\frac{k}{c}\text{ when }k>0 \quad\text{and}\quad \frac{y^2}{b^2}-\frac{x^2}{a^2}=\frac{k}{c}\text{ when }k<0} . The horizontal trace is a hyperbola.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{c}=\frac{x^2}{a^2}-\frac{k^2}{b^2}\quad y=k} . The vertical trace is a parabola.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{c}=\frac{k^2}{a^2}-\frac{y^2}{b^2}\quad x=k} . The vertical trace is a parabola.

Cone, hyperboloid of one sheet, and hyperboloid of two sheets

An image of a hyperboloid of one sheet.

An image of a hyperboloid of two sheets. Note that horizontal traces in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=k} are ellipses if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k>c} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k<-c} .

Cones have the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z^2}{c^2}=\frac{x^2}{a^2}+\frac{y^2}{b^2}}

Note that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=0} when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=0} .

Hyperboloids of one sheet have the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1}

Note that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1} when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=0} .

Hyperboloids of two sheets have the equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1}

Note that when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -c\leq z\leq c} , there is no real solution for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,y} .

All of the three quadric surfaces have the same respective traces. The horizontal traces are all ellipses and the vertical traces are all hyperbolas.

Resources

• Equations of Lines and Planes in Space, Mathematics LibreTexts
• Quadric Surfaces, OpenStax
• Equations of Lines, Paul's Online Notes
• Equations of Planes, Paul's Online Notes
• Quadric Surfaces, Paul's Online Notes

Licensing

Content obtained and/or adapted from:

• Curves and Surfaces in Space, Wikibooks: Calculus under a CC BY-SA license