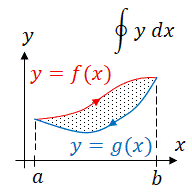
Area between Curves

Introduction

Finding the area between two curves, usually given by two explicit functions, is often useful in calculus.

In general the rule for finding the area between two curves is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=A_{\rm top}-A_{\rm bottom}} or

If f(x) is the upper function and g(x) is the lower function

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\int\limits_a^b \bigl(f(x)-g(x)\bigr)dx}

This is true whether the functions are in the first quadrant or not.

Area between two curves

Suppose we are given two functions Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1=f(x)} and $y_{2}=g(x)$ and we want to find the area between them on the interval $[a,b]$ . Also assume that $f(x)\geq g(x)$ for all $x$ on the interval $[a,b]$ . Begin by partitioning the interval $[a,b]$ into $n$ equal subintervals each having a length of $\Delta x={\frac {b-a}{n}}$ . Next choose any point in each subinterval, $x_{i}^{*}$ . Now we can 'create' rectangles on each interval. At the point $x_{i}*$ , the height of each rectangle is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_i^*)-g(x_i^*)} and the width is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} . Thus the area of each rectangle is ${\bigl [}f(x_{i}^{*})-g(x_{i}^{*}){\bigr ]}\Delta x$ . An approximation of the area, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} , between the two curves is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A:=\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x} .

Now we take the limit as $n$ approaches infinity and get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(x_i^*)-g(x_i^*)\Big]\Delta x}

which gives the exact area. Recalling the definition of the definite integral we notice that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\int\limits_a^b \bigl(f(x)-g(x)\bigr)dx} .

This formula of finding the area between two curves is sometimes known as applying integration with respect to the x-axis since the rectangles used to approximate the area have their bases lying parallel to the x-axis. It will be most useful when the two functions are of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1=f(x)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_2=g(x)} . Sometimes however, one may find it simpler to integrate with respect to the y-axis. This occurs when integrating with respect to the x-axis would result in more than one integral to be evaluated. These functions take the form $x_{1}=f(y)$ and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=g(y)} on the interval $[c,d]$ . Note that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [c,d]} are values of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} . The derivation of this case is completely identical. Similar to before, we will assume that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y)\ge g(y)} for all $y$ on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [c,d]} . Now, as before we can divide the interval into Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} subintervals and create rectangles to approximate the area between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(y)} . It may be useful to picture each rectangle having their 'width', $\Delta y$ , parallel to the y-axis and 'height', Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y_i^*)-g(y_i^*)} at the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_i^*} , parallel to the x-axis. Following from the work above we may reason that an approximation of the area, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} , between the two curves is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A:=\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y} .

As before, we take the limit as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} approaches infinity to arrive at

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\lim_{n\to\infty}\sum_{i=1}^n \Big[f(y_i^*)-g(y_i^*)\Big]\Delta y} ,

which is nothing more than a definite integral, so