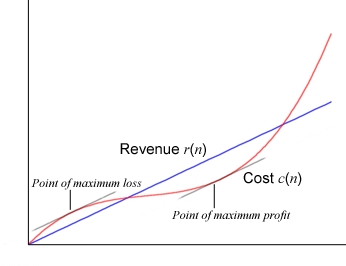
File:Calculus Graph-Finding Maximum Profit.png
Jump to navigation
Jump to search
No higher resolution available.
Calculus_Graph-Finding_Maximum_Profit.png (346 × 266 pixels, file size: 6 KB, MIME type: image/png)
Summary
| Description |
English: This graphic was made by me with Adobe Photoshop CS (manually) after using Maxima to find an approximate graph of the equations f(x)=8.1x and g(x)=n^3-7n^2+18n. |
| Date | 24 October 2005 (original upload date) |
| Source | Transferred from en.wikibooks to Commons by Adrignola using CommonsHelper. |
| Author | Usurper at English Wikibooks |
Licensing
|
This work has been released into the public domain by its author, Usurper, at the English Wikipedia project. This applies worldwide. In case this is not legally possible: |
Original upload log
The original description page was here. All following user names refer to en.wikibooks.
- 2005-10-24 23:50 Usurper 346×266× (5806 bytes) This graphic was made by me with Adobe Photoshop CS (manually) after using Maxima to find an approximate graph of the equations f(x)=8.1x and g(x)=n^3-7n^2+18n.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 20:50, 12 July 2010 | | 346 × 266 (6 KB) | File Upload Bot (Magnus Manske) | {{BotMoveToCommons|en.wikibooks|year={{subst:CURRENTYEAR}}|month={{subst:CURRENTMONTHNAME}}|day={{subst:CURRENTDAY}}}} {{Information |Description={{en|This graphic was made by me with Adobe Photoshop CS (manually) after using Maxima to find an approximat |
File usage
The following page uses this file:
