Difference between revisions of "Cyclic Groups"
| (6 intermediate revisions by the same user not shown) | |||
| Line 31: | Line 31: | ||
|colspan=2|Two frieze groups are isomorphic to '''Z'''. With one generator, p1 has translations and p11g has glide reflections. | |colspan=2|Two frieze groups are isomorphic to '''Z'''. With one generator, p1 has translations and p11g has glide reflections. | ||
|} | |} | ||
| − | On the other hand, in an '''infinite cyclic group''' ''G ='' ⟨''g''⟩'','' the powers ''g''<sup>''k''</sup> give distinct elements for all integers ''k'', so that ''G'' = { ... , ''g''<sup>−2</sup>, ''g''<sup>−1</sup>, ''e'', ''g'', ''g''<sup>2</sup>, ... }, and ''G'' is isomorphic to the standard group C = C<sub>∞</sub> and to '''Z''', the additive group of the integers. An example is the first frieze group. Here there are no finite cycles, and the name "cyclic" may be misleading. | + | On the other hand, in an '''infinite cyclic group''' ''G ='' ⟨''g''⟩'','' the powers ''g''<sup>''k''</sup> give distinct elements for all integers ''k'', so that ''G'' = { ... , ''g''<sup>−2</sup>, ''g''<sup>−1</sup>, ''e'', ''g'', ''g''<sup>2</sup>, ... }, and ''G'' is isomorphic to the standard group C = C<sub>∞</sub> and to '''Z''', the additive group of the integers. An example is the first frieze group. Here there are no finite cycles, and the name "cyclic" may be misleading. |
To avoid this confusion, Bourbaki introduced the term '''monogenous group''' for a group with a single generator and restricted "cyclic group" to mean a finite monogenous group, avoiding the term "infinite cyclic group". | To avoid this confusion, Bourbaki introduced the term '''monogenous group''' for a group with a single generator and restricted "cyclic group" to mean a finite monogenous group, avoiding the term "infinite cyclic group". | ||
| Line 37: | Line 37: | ||
==Examples== | ==Examples== | ||
===Integer and modular addition=== | ===Integer and modular addition=== | ||
| − | The set of integers '''Z''', with the operation of addition, forms a group. | + | The set of integers '''Z''', with the operation of addition, forms a group. It is an '''infinite cyclic group''', because all integers can be written by repeatedly adding or subtracting the single number 1. In this group, 1 and −1 are the only generators. Every infinite cyclic group is isomorphic to '''Z'''. |
For every positive integer ''n'', the set of integers modulo ''n'', again with the operation of addition, forms a finite cyclic group, denoted '''Z'''/''n'''''Z'''. | For every positive integer ''n'', the set of integers modulo ''n'', again with the operation of addition, forms a finite cyclic group, denoted '''Z'''/''n'''''Z'''. | ||
| Line 139: | Line 139: | ||
===Cayley graph=== | ===Cayley graph=== | ||
| − | + | ||
[[File:Paley13.svg|thumb|240px|The Paley graph of order 13, a circulant graph formed as the Cayley graph of '''Z'''/13 with generator set {1,3,4}]] | [[File:Paley13.svg|thumb|240px|The Paley graph of order 13, a circulant graph formed as the Cayley graph of '''Z'''/13 with generator set {1,3,4}]] | ||
A Cayley graph is a graph defined from a pair (''G'',''S'') where ''G'' is a group and ''S'' is a set of generators for the group; it has a vertex for each group element, and an edge for each product of an element with a generator. In the case of a finite cyclic group, with its single generator, the Cayley graph is a cycle graph, and for an infinite cyclic group with its generator the Cayley graph is a doubly infinite path graph. However, Cayley graphs can be defined from other sets of generators as well. The Cayley graphs of cyclic groups with arbitrary generator sets are called circulant graphs. These graphs may be represented geometrically as a set of equally spaced points on a circle or on a line, with each point connected to neighbors with the same set of distances as each other point. They are exactly the vertex-transitive graphs whose symmetry group includes a transitive cyclic group. | A Cayley graph is a graph defined from a pair (''G'',''S'') where ''G'' is a group and ''S'' is a set of generators for the group; it has a vertex for each group element, and an edge for each product of an element with a generator. In the case of a finite cyclic group, with its single generator, the Cayley graph is a cycle graph, and for an infinite cyclic group with its generator the Cayley graph is a doubly infinite path graph. However, Cayley graphs can be defined from other sets of generators as well. The Cayley graphs of cyclic groups with arbitrary generator sets are called circulant graphs. These graphs may be represented geometrically as a set of equally spaced points on a circle or on a line, with each point connected to neighbors with the same set of distances as each other point. They are exactly the vertex-transitive graphs whose symmetry group includes a transitive cyclic group. | ||
===Endomorphisms=== | ===Endomorphisms=== | ||
| − | The endomorphism ring of the abelian group '''Z'''/''n'''''Z''' is isomorphic to '''Z'''/''n'''''Z''' itself as a ring. Under this isomorphism, the number ''r'' corresponds to the endomorphism of '''Z'''/''n'''''Z''' that maps each element to the sum of ''r'' copies of it. This is a bijection if and only if ''r'' is coprime with ''n'', so the automorphism group of '''Z'''/''n'''''Z''' is isomorphic to the unit group ('''Z'''/''n'''''Z''')<sup>×</sup>.< | + | The endomorphism ring of the abelian group '''Z'''/''n'''''Z''' is isomorphic to '''Z'''/''n'''''Z''' itself as a ring. Under this isomorphism, the number ''r'' corresponds to the endomorphism of '''Z'''/''n'''''Z''' that maps each element to the sum of ''r'' copies of it. This is a bijection if and only if ''r'' is coprime with ''n'', so the automorphism group of '''Z'''/''n'''''Z''' is isomorphic to the unit group ('''Z'''/''n'''''Z''')<sup>×</sup>. |
| + | |||
| + | Similarly, the endomorphism ring of the additive group of '''Z''' is isomorphic to the ring '''Z'''. Its automorphism group is isomorphic to the group of units of the ring '''Z''', which is ({−1, +1}, ×) ≅ C<sub>2</sub>. | ||
| + | |||
| + | ==Basic Theorems Regarding Cyclic Groups== | ||
| + | <p>If <span class="math-inline"><math>G</math></span> is a group then <span class="math-inline"><math>G</math></span> is said to be cyclic if there exists an <span class="math-inline"><math>a \in G</math></span> such that <span class="math-inline"><math>G = \langle a \rangle</math></span>, that is, every element of <span class="math-inline"><math>G</math></span> is of the form <span class="math-inline"><math>a^n</math></span> for some <span class="math-inline"><math>n \in \mathbb{Z}</math></span>. We will now look at some basic results regarding cyclic groups.</p> | ||
| + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | ||
| + | <td><strong>Theorem 1:</strong> If <span class="math-inline"><math>G</math></span> is an infinite cyclic group then <span class="math-inline"><math>G</math></span> is isomorphic to <span class="math-inline"><math>(\mathbb{Z}, +)</math></span>.</td> | ||
| + | </blockquote> | ||
| + | <ul> | ||
| + | <li><strong>Proof:</strong> Let <span class="math-inline"><math>G</math></span> be an infinite cyclic group and write <span class="math-inline"><math>G = \langle a \rangle</math></span>. If <span class="math-inline"><math>g \in G</math></span> then there exists a unique <span class="math-inline"><math>n \in \mathbb{Z}</math></span> such that <span class="math-inline"><math>g = a^n</math></span>. Immediately, we see that <span class="math-inline"><math>|G|</math></span> is countably infinite.</li> | ||
| + | </ul> | ||
| + | <ul> | ||
| + | <li>Let <span class="math-inline"><math>\varphi : G \to \mathbb{Z}</math></span> be defined for each <span class="math-inline"><math>g = a^{n(g)} \in G</math></span> by:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad \varphi(g) = \varphi(a^{g(n)}) := n(g) \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>Then <span class="math-inline"><math>\varphi</math></span> is a homomorphism from <span class="math-inline"><math>G = \langle a \rangle</math></span> to <span class="math-inline"><math>(\mathbb{Z}, +)</math></span> since for all <span class="math-inline"><math>g_1 = a^{n(g_1)}, g_2 = a^{n(g_2)} \in G</math></span> we have by the laws of exponents that:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad \varphi(g_1 \cdot g_2) = \varphi(a^{n(g_1)}a^{n(g_2)}) = \varphi(a^{n(g_1) + n(g_2)}) = n(g_1) + n(g_2) = \varphi(g_1) + \varphi(g_2) \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>Let <span class="math-inline"><math>g_1 = a^{n(g_1)}, g_2 = a^{n(g_2)} \in G</math></span> and suppose that <span class="math-inline"><math>\varphi(g_1) = \varphi(g_2) </math></span>. Then <span class="math-inline"><math> n(g_1) = n(g_2)</math></span>, so <span class="math-inline"><math>g_1 = a^{n(g_1}) = a^{n(g_2)} = g_2</math></span>, so <span class="math-inline"><math>\varphi</math></span> is injective.</li> | ||
| + | </ul> | ||
| + | <ul> | ||
| + | <li>Furthermore, if <span class="math-inline"><math>n \in \mathbb{Z}</math></span> then <span class="math-inline"><math>a^{n}</math></span> is such that <span class="math-inline"><math>\varphi(g^n) = n</math></span>, so <span class="math-inline"><math>\varphi</math></span> is surjective.</li> | ||
| + | </ul> | ||
| + | <ul> | ||
| + | <li>Thus <span class="math-inline"><math>\varphi : G \to \mathbb{Z}</math></span> is an isomorphism of <span class="math-inline"><math>G = \langle a \rangle</math></span> to <span class="math-inline"><math>(\mathbb{Z}, +)</math></span>. <span class="math-inline"><math>\blacksquare</math></span></li> | ||
| + | </ul> | ||
| + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | ||
| + | <td><strong>Theorem 2:</strong> If <span class="math-inline"><math>G</math></span> is a finite cyclic group of order <span class="math-inline"><math>n</math></span> then <span class="math-inline"><math>G</math></span> is isomorphic to <span class="math-inline"><math>(\mathbb{Z}/n\mathbb{Z}, +)</math></span>.</td> | ||
| + | </blockquote> | ||
| + | <ul> | ||
| + | <li><strong>Proof:</strong> Suppose that <span class="math-inline"><math>G = \langle a \rangle</math></span>. Then <span class="math-inline"><math>G = \{ a^0, a^1, ..., a^{n-1} \}</math></span>. Let <span class="math-inline"><math>\varphi : G \to \mathbb{Z}/n\mathbb{Z}</math></span> be defined by:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad \varphi(a^i) = [i] \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>Then <span class="math-inline"><math>\varphi</math></span> is a homomorphism since if <span class="math-inline"><math>a^i, a^j \in G</math></span> is such that <span class="math-inline"><math>i + j \leq n-1</math></span> then:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad \varphi(a^i \cdot a^j) = \varphi (a^{i+j}) = [i] + [j]= \varphi(a^i) + \varphi(a^j) \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>And if <span class="math-inline"><math>a^i, a^j \in G</math></span> is such that <span class="math-inline"><math>i + j > n-1</math></span> then we can write <span class="math-inline"><math>i + j = qn + r</math></span> where <span class="math-inline"><math>q \geq 1</math></span> and <span class="math-inline"><math>0 \leq r < n</math></span> (by the division algorithm) so that:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad \varphi(a^i \cdot a^j) = \varphi(a^{i+j}) = \varphi(a^{qn + r}) = \varphi((a^n)^qa^r) = \varphi(1^qa^r) = \varphi(a^r) = [r] = [qn + r] = [i +j] \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>It is easy to see that <span class="math-inline"><math>\varphi</math></span> is injective and surjective, so <span class="math-inline"><math>\varphi</math></span> is an isomorphism of <span class="math-inline"><math>G = \langle a \rangle</math></span> and <span class="math-inline"><math>(\mathbb{Z}/n\mathbb{Z}, +)</math></span>. <span class="math-inline"><math>\blacksquare</math></span></li> | ||
| + | </ul> | ||
| + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | ||
| + | <td><strong>Proposition 3:</strong> Two finite cyclic groups <span class="math-inline"><math>G_1</math></span> and <span class="math-inline"><math>G_2</math></span> are isomorphic if and only if they are of the same order.</td> | ||
| + | </blockquote> | ||
| + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | ||
| + | <td><strong>Proposition 4:</strong> If <span class="math-inline"><math>G</math></span> is a cyclic group and <span class="math-inline"><math>H</math></span> is a subgroup of <span class="math-inline"><math>G</math></span> then <span class="math-inline"><math>H</math></span> is also cyclic group. Furthermore, if <span class="math-inline"><math>G</math></span> is a finite cyclic group of order <span class="math-inline"><math>n</math></span> then for each <span class="math-inline"><math>k \in \mathbb{N}</math></span> with <span class="math-inline"><math>k | n</math></span> there exists a unique subgroup <span class="math-inline"><math>H</math></span> of <span class="math-inline"><math>G</math></span> with <span class="math-inline"><math>|H| = k</math></span>.</td> | ||
| + | </blockquote> | ||
| + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> <td><strong>Proposition 5:</strong> Let <span class="math-inline"><math>G</math></span> be a finite cyclic group of order <span class="math-inline"><math>n</math></span> with <span class="math-inline"><math>G = \langle a \rangle</math></span>. Then <span class="math-inline"><math>G</math></span> is generated by <span class="math-inline"><math>a^k</math></span> if and only if <span class="math-inline"><math>\mathrm{gcd}(n, k) = 1</math></span>.</td> | ||
| + | </blockquote> | ||
| − | + | ==Subgroups of Cyclic Groups are Cyclic Groups== | |
| + | <p>A group <span class="math-inline"><math>G</math></span> is said to be a cyclic group if <span class="math-inline"><math>G = \langle a \rangle = \{ a^n : n \in \mathbb{Z} \}</math></span> for some <span class="math-inline"><math>a \in G</math></span>, i.e., <span class="math-inline"><math>G</math></span> can be generated by a single element <span class="math-inline"><math>a \in G</math></span>.</p> | ||
| + | <p>We will now prove an important theorem - every subgroup of a cyclic group is also cyclic.</p> | ||
| + | <blockquote style="background: white; border: 1px solid black; padding: 1em;"> | ||
| + | <td><strong>Theorem 1:</strong> Let <span class="math-inline"><math>G</math></span> be a cyclic group. Then any subgroup <span class="math-inline"><math>H</math></span> of <span class="math-inline"><math>G</math></span> is also a cyclic group.</td> | ||
| + | </blockquote> | ||
| + | <p><em>The converse of Theorem 1 is not true in general, i.e., even if every proper subgroup <span class="math-inline"><math>H</math></span> of a group <span class="math-inline"><math>G</math></span> is cyclic - it might be the case that <span class="math-inline"><math>G</math></span> is not cyclic. The simplest example of this is the group <span class="math-inline"><math>\mathbb{Z}_2 \times \mathbb{Z}_2</math></span>. The only proper subgroups of this group are the trivial group and <span class="math-inline"><math>\mathbb{Z}_2</math></span> - both of which are cyclic. But it is easy to check that <span class="math-inline"><math>\mathbb{Z}_2 \times \mathbb{Z}_2</math></span> is not cyclic.</em></p> | ||
| + | <ul> | ||
| + | <li><strong>Proof:</strong> Let <span class="math-inline"><math>G</math></span> be a cyclic group. Then there exists an <span class="math-inline"><math>a \in G</math></span> such that <span class="math-inline"><math>G = \langle a \rangle</math></span>. Let <span class="math-inline"><math>H</math></span> be a subgroup of <span class="math-inline"><math>G</math></span>.</li> | ||
| + | </ul> | ||
| + | <ul> | ||
| + | <li>If <span class="math-inline"><math>H</math></span> is the trivial subgroup, then clearly <span class="math-inline"><math>H = \langle e \rangle</math></span>, and so <span class="math-inline"><math>H</math></span> is a cyclic group.</li> | ||
| + | </ul> | ||
| + | <ul> | ||
| + | <li>If <span class="math-inline"><math>H</math></span> is not the trivial subgroup then there exists a <span class="math-inline"><math>b \in H</math></span> such that <span class="math-inline"><math>b \neq e</math></span>. Since <span class="math-inline"><math>b \in H \subseteq G = \langle a \rangle</math></span>, there exists an <span class="math-inline"><math>n \in \mathbb{Z}</math></span> such that <span class="math-inline"><math>b = a^n</math></span>, and <span class="math-inline"><math>n \neq 0</math></span>. Since <span class="math-inline"><math>H</math></span> is itself a group and <span class="math-inline"><math>b \in H</math></span> we have that <span class="math-inline"><math>b^{-1} = (a^n)^{-1} = a^{-n} \in H</math></span> with <span class="math-inline"><math>-n \neq 0</math></span>.</li> | ||
| + | </ul> | ||
| + | <ul> | ||
| + | <li>So there exists an element <span class="math-inline"><math>a^k \in H</math></span> with <span class="math-inline"><math>k > 0</math></span>. Consider the set <span class="math-inline"><math>K = \{ k : a^k \in H, \; k > 0 \}</math></span>. This set is a nonempty subset of <span class="math-inline"><math>\mathbb{N}</math></span>, and so by the Well-Ordering principle, it contains a least element, call it <span class="math-inline"><math>\tilde{k}</math></span>.</li> | ||
| + | </ul> | ||
| + | <ul> | ||
| + | <li>Now since <span class="math-inline"><math>a^{\tilde{k}} \in H</math></span> and <span class="math-inline"><math>H</math></span> is a group, we have that <span class="math-inline"><math>\langle a^{\tilde{k}} \rangle \subseteq H</math></span>. S let <span class="math-inline"><math>h \in H</math></span>. Since <span class="math-inline"><math>H \subseteq G</math></span> we have that <span class="math-inline"><math>h \in G</math></span>. So <span class="math-inline"><math>h = a^m</math></span> for some <span class="math-inline"><math>m \in \mathbb{Z}</math></span>. Using the division algorithm on <span class="math-inline"><math>m</math></span> and <span class="math-inline"><math>\tilde{k}</math></span>, we see that there exists integers <span class="math-inline"><math>q, r</math></span> such that:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad m = \tilde{k}q + r \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>With <span class="math-inline"><math>0 \leq r < \tilde{k}</math></span>. But then:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad h = a^m = a^{\tilde{k}q + r} = a^{\tilde{k}q} a^r = (a^{\tilde{k}})^q a^r = (a^{\tilde{k}})^q a^r \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>Since <span class="math-inline"><math>h \in H</math></span> and <span class="math-inline"><math>(a^{\tilde{k}})^q \in H</math></span> we see that:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad a^r = (a^{\tilde{k}})^{-q} h \in H \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>If <span class="math-inline"><math>r > 0</math></span>, then <span class="math-inline"><math>r \in K = \{ k : a^k \in H, k > 0 \}</math></span>. But <span class="math-inline"><math>r < \tilde{k}</math></span>, which contradicts the minimality of <span class="math-inline"><math>\tilde{k}</math></span> in <span class="math-inline"><math>K</math></span>. So we must have that <span class="math-inline"><math>r = 0</math></span>. So:</li> | ||
| + | </ul> | ||
| + | <div style="text-align: center;"><math>\begin{align} \quad a^0 &= (a^{\tilde{k}})^{-q} h \\ \quad e &= (a^{\tilde{k}})^{-q} h \\ \quad h &= (a^{\tilde{k}})^q \end{align}</math></div> | ||
| + | <ul> | ||
| + | <li>Thus <span class="math-inline"><math>h \in \langle a^{\tilde{k}}</math></span>, showing that <span class="math-inline"><math>H \subseteq \langle a^{\tilde{k}}</math></span>. Thus we conclude that <span class="math-inline"><math>H = \langle a^{\tilde{k}}</math></span>, i.e., <span class="math-inline"><math>H</math></span> is a cyclic group. <span class="math-inline"><math>\blacksquare</math></span></li> | ||
| + | </ul> | ||
== Licensing == | == Licensing == | ||
Content obtained and/or adapted from: | Content obtained and/or adapted from: | ||
* [https://en.wikipedia.org/wiki/Cyclic_group Cyclic group, Wikipedia] under a CC BY-SA license | * [https://en.wikipedia.org/wiki/Cyclic_group Cyclic group, Wikipedia] under a CC BY-SA license | ||
| + | * [http://mathonline.wikidot.com/basic-theorems-regarding-cyclic-groups Basic Theorems Regarding Cyclic Groups, mathonline.wikidot.com] under a CC BY-SA license | ||
Latest revision as of 13:22, 17 November 2021
A cyclic group or monogenous group is a group that is generated by a single element. That is, it is a set of invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as a power of g in multiplicative notation, or as a multiple of g in additive notation. This element g is called a generator of the group.
Every infinite cyclic group is isomorphic to the additive group of Z, the integers. Every finite cyclic group of order n is isomorphic to the additive group of Z/nZ, the integers modulo n. Every cyclic group is an abelian group (meaning that its group operation is commutative), and every finitely generated abelian group is a direct product of cyclic groups.
Every cyclic group of prime order is a simple group, which cannot be broken down into smaller groups. In the classification of finite simple groups, one of the three infinite classes consists of the cyclic groups of prime order. The cyclic groups of prime order are thus among the building blocks from which all groups can be built.
Contents
Definition and notation
For any element g in any group G, one can form a subgroup of all integer powers ⟨g⟩ = {gk | k ∈ Z}, called a cyclic subgroup of g. The order of g is the number of elements in ⟨g⟩; that is, the order of an element is equal to the order of its cyclic subgroup.
A cyclic group is a group which is equal to one of its cyclic subgroups: G = ⟨g⟩ for some element g, called a generator.
For a finite cyclic group G of order n we have G = {e, g, g2, ... , gn−1}, where e is the identity element and gi = gj whenever i ≡ j (mod n); in particular gn = g0 = e, and g−1 = gn−1. An abstract group defined by this multiplication is often denoted Cn, and we say that G is isomorphic to the standard cyclic group Cn. Such a group is also isomorphic to Z/nZ, the group of integers modulo n with the addition operation, which is the standard cyclic group in additive notation. Under the isomorphism χ defined by χ(gi) = i the identity element e corresponds to 0, products correspond to sums, and powers correspond to multiples.
For example, the set of complex 6th roots of unity
forms a group under multiplication. It is cyclic, since it is generated by the primitive root that is, G = ⟨z⟩ = { 1, z, z2, z3, z4, z5 } with z6 = 1. Under a change of letters, this is isomorphic to (structurally the same as) the standard cyclic group of order 6, defined as C6 = ⟨g⟩ = { e, g, g2, g3, g4, g5 } with multiplication gj · gk = gj+k (mod 6), so that g6 = g0 = e. These groups are also isomorphic to Z/6Z = {0,1,2,3,4,5} with the operation of addition modulo 6, with zk and gk corresponding to k. For example, 1 + 2 ≡ 3 (mod 6) corresponds to z1 · z2 = z3, and 2 + 5 ≡ 1 (mod 6) corresponds to z2 · z5 = z7 = z1, and so on. Any element generates its own cyclic subgroup, such as ⟨z2⟩ = { e, z2, z4 } of order 3, isomorphic to C3 and Z/3Z; and ⟨z5⟩ = { e, z5, z10 = z4, z15 = z3, z20 = z2, z25 = z } = G, so that z5 has order 6 and is an alternative generator of G.
Instead of the quotient] notations Z/nZ, Z/(n), or Z/n, some authors denote a finite cyclic group as Zn, but this conflicts with the notation of number theory, where Zp denotes a p-adic number ring, or localization at a prime ideal.
| *∞∞]]) | p11g, (22∞) |
|---|---|

|

|
| Two frieze groups are isomorphic to Z. With one generator, p1 has translations and p11g has glide reflections. | |
On the other hand, in an infinite cyclic group G = ⟨g⟩, the powers gk give distinct elements for all integers k, so that G = { ... , g−2, g−1, e, g, g2, ... }, and G is isomorphic to the standard group C = C∞ and to Z, the additive group of the integers. An example is the first frieze group. Here there are no finite cycles, and the name "cyclic" may be misleading.
To avoid this confusion, Bourbaki introduced the term monogenous group for a group with a single generator and restricted "cyclic group" to mean a finite monogenous group, avoiding the term "infinite cyclic group".
Examples
Integer and modular addition
The set of integers Z, with the operation of addition, forms a group. It is an infinite cyclic group, because all integers can be written by repeatedly adding or subtracting the single number 1. In this group, 1 and −1 are the only generators. Every infinite cyclic group is isomorphic to Z.
For every positive integer n, the set of integers modulo n, again with the operation of addition, forms a finite cyclic group, denoted Z/nZ. A modular integer i is a generator of this group if i is relatively prime to n, because these elements can generate all other elements of the group through integer addition. (The number of such generators is φ(n), where φ is the Euler totient function.) Every finite cyclic group G is isomorphic to Z/nZ, where n = |G| is the order of the group.
The addition operations on integers and modular integers, used to define the cyclic groups, are the addition operations of commutative rings, also denoted Z and Z/nZ or Z/(n). If p is a prime, then Z/pZ is a finite field, and is usually denoted Fp or GF(p) for Galois field.
Modular multiplication
For every positive integer n, the set of the integers modulo n that are relatively prime to n is written as (Z/nZ)×; it forms a group under the operation of multiplication. This group is not always cyclic, but is so whenever n is 1, 2, 4, a power of an odd prime, or twice a power of an odd prime.
This is the multiplicative group of units of the ring Z/nZ; there are φ(n) of them, where again φ is the Euler totient function. For example, (Z/6Z)× = {1,5}, and since 6 is twice an odd prime this is a cyclic group. In contrast, (Z/8Z)× = {1,3,5,7} is a Klein 4-group and is not cyclic. When (Z/nZ)× is cyclic, its generators are called primitive roots modulo n.
For a prime number p, the group (Z/pZ)× is always cyclic, consisting of the non-zero elements of the finite field of order p. More generally, every finite subgroup of the multiplicative group of any field is cyclic.
Rotational symmetries
The set of rotational symmetries of a polygon forms a finite cyclic group. If there are n different ways of moving the polygon to itself by a rotation (including the null rotation) then this symmetry group is isomorphic to Z/nZ. In three or higher dimensions there exist other finite symmetry groups that are cyclic, but which are not all rotations around an axis, but instead rotoreflections.
The group of all rotations of a circle S1 (the circle group, also denoted S1) is not cyclic, because there is no single rotation whose integer powers generate all rotations. In fact, the infinite cyclic group C∞ is countable, while S1 is not. The group of rotations by rational angles is countable, but still not cyclic.
Galois theory
An nth root of unity is a complex number whose nth power is 1, a root of the polynomial xn − 1. The set of all nth roots of unity form a cyclic group of order n under multiplication. For example, the polynomial z3 − 1 factors as (z − 1)(z − ω)(z − ω2), where ω = e2πi/3; the set {1, ω, ω2} = {ω0, ω1, ω2} forms a cyclic group under multiplication. The Galois group of the field extension of the rational numbers generated by the nth roots of unity forms a different group, isomorphic to the multiplicative group (Z/nZ)× of order φ(n), which is cyclic for some but not all n (see above).
A field extension is called a cyclic extension if its Galois group is cyclic. For fields of characteristic zero, such extensions are the subject of Kummer theory, and are intimately related to solvability by radicals. For an extension of finite fields of characteristic p, its Galois group is always finite and cyclic, generated by a power of the Frobenius mapping.
Subgroups
All subgroups and quotient groups of cyclic groups are cyclic. Specifically, all subgroups of Z are of the form ⟨m⟩ = mZ, with m a positive integer. All of these subgroups are distinct from each other, and apart from the trivial group {0} = 0Z, they all are isomorphic to Z. The lattice of subgroups of Z is isomorphic to the dual of the lattice of natural numbers ordered by divisibility. Thus, since a prime number p has no nontrivial divisors, pZ is a maximal proper subgroup, and the quotient group Z/pZ is simple; in fact, a cyclic group is simple if and only if its order is prime.
All quotient groups Z/nZ are finite, with the exception Z/0Z = Z/{0}. For every positive divisor d of n, the quotient group Z/nZ has precisely one subgroup of order d, generated by the residue class of n/d. There are no other subgroups.
Additional properties
Every cyclic group is abelian. That is, its group operation is commutative: gh = hg (for all g and h in G). This is clear for the groups of integer and modular addition since r + s ≡ s + r (mod n), and it follows for all cyclic groups since they are all isomorphic to these standard groups. For a finite cyclic group of order n, gn is the identity element for any element g. This again follows by using the isomorphism to modular addition, since kn ≡ 0 (mod n) for every integer k. (This is also true for a general group of order n, due to Lagrange's theorem.)
For a prime power pk, the group Z/pkZ is called a primary cyclic group. The fundamental theorem of abelian groups states that every finitely generated abelian group is a finite direct product of primary cyclic and infinite cyclic groups.
Because a cyclic group is abelian, each of its conjugacy classes consists of a single element. A cyclic group of order n therefore has n conjugacy classes.
If d is a divisor of n, then the number of elements in Z/nZ which have order d is φ(d), and the number of elements whose order divides d is exactly d. If G is a finite group in which, for each n > 0, G contains at most n elements of order dividing n, then G must be cyclic. (And observe that when n is prime, there is exactly one element whose order is a proper divisor of n, namely the identity.)}} The order of an element m in Z/nZ is n/gcd(n,m).
If n and m are coprime, then the direct product of two cyclic groups Z/nZ and Z/mZ is isomorphic to the cyclic group Z/nmZ, and the converse also holds: this is one form of the Chinese remainder theorem. For example, Z/12Z is isomorphic to the direct product Z/3Z × Z/4Z under the isomorphism (k mod 12) → (k mod 3, k mod 4); but it is not isomorphic to Z/6Z × Z/2Z, in which every element has order at most 6.
If p is a prime number, then any group with p elements is isomorphic to the simple group Z/pZ. A number n is called a cyclic number if Z/nZ is the only group of order n, which is true exactly when gcd(n,φ(n)) = 1. The cyclic numbers include all primes, but some are composite such as 15. However, all cyclic numbers are odd except 2. The cyclic numbers are:
- 1, 2, 3, 5, 7, 11, 13, 15, 17, 19, 23, 29, 31, 33, 35, 37, 41, 43, 47, 51, 53, 59, 61, 65, 67, 69, 71, 73, 77, 79, 83, 85, 87, 89, 91, 95, 97, 101, 103, 107, 109, 113, 115, 119, 123, 127, 131, 133, 137, 139, 141, 143, ...
The definition immediately implies that cyclic groups have group presentation and for finite n.
Associated objects
Representations
The representation theory of the cyclic group is a critical base case for the representation theory of more general finite groups. In the complex case, a representation of a cyclic group decomposes into a direct sum of linear characters, making the connection between character theory and representation theory transparent. In the positive characteristic case, the indecomposable representations of the cyclic group form a model and inductive basis for the representation theory of groups with cyclic Sylow subgroups and more generally the representation theory of blocks of cyclic defect.
Cycle graph
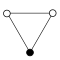
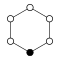
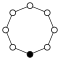
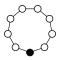
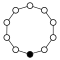
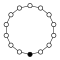
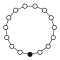
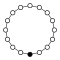
A cycle graph illustrates the various cycles of a group and is particularly useful in visualizing the structure of small finite groups. A cycle graph for a cyclic group is simply a circular graph, where the group order is equal to the number of nodes. A single generator defines the group as a directional path on the graph, and the inverse generator defines a backwards path. Trivial paths (identity) can be drawn as a loop but are usually suppressed. Z2 is sometimes drawn with two curved edges as a multigraph.
A cyclic groups Zn, with order n, corresponds to a single cycle graphed simply as an n-sided polygon with the elements at the vertices.

|
|

|

|
|

|
| |
| Z1 | Z2 | Z3 | Z4 | Z5 | Z6 = Z3×Z2 | Z7 | Z8 |
|
|

|

|

|
|
|
|
| Z9 | Z10 = Z5×Z2 | Z11 | Z12 = Z4×Z3 | Z13 | Z14 = Z7×Z2 | Z15 = Z5×Z3 | Z16 |

|

|

|

|

|

|

|

|
| Z17 | Z18 = Z9×Z2 | Z19 | Z20 = Z5×Z4 | Z21 = Z7×Z3 | Z22 = Z11×Z2 | Z23 | Z24 = Z8×Z3 |
Cayley graph
A Cayley graph is a graph defined from a pair (G,S) where G is a group and S is a set of generators for the group; it has a vertex for each group element, and an edge for each product of an element with a generator. In the case of a finite cyclic group, with its single generator, the Cayley graph is a cycle graph, and for an infinite cyclic group with its generator the Cayley graph is a doubly infinite path graph. However, Cayley graphs can be defined from other sets of generators as well. The Cayley graphs of cyclic groups with arbitrary generator sets are called circulant graphs. These graphs may be represented geometrically as a set of equally spaced points on a circle or on a line, with each point connected to neighbors with the same set of distances as each other point. They are exactly the vertex-transitive graphs whose symmetry group includes a transitive cyclic group.
Endomorphisms
The endomorphism ring of the abelian group Z/nZ is isomorphic to Z/nZ itself as a ring. Under this isomorphism, the number r corresponds to the endomorphism of Z/nZ that maps each element to the sum of r copies of it. This is a bijection if and only if r is coprime with n, so the automorphism group of Z/nZ is isomorphic to the unit group (Z/nZ)×.
Similarly, the endomorphism ring of the additive group of Z is isomorphic to the ring Z. Its automorphism group is isomorphic to the group of units of the ring Z, which is ({−1, +1}, ×) ≅ C2.
Basic Theorems Regarding Cyclic Groups
If is a group then is said to be cyclic if there exists an such that , that is, every element of is of the form for some . We will now look at some basic results regarding cyclic groups.
Theorem 1: If is an infinite cyclic group then is isomorphic to .
- Proof: Let be an infinite cyclic group and write . If then there exists a unique such that . Immediately, we see that is countably infinite.
- Let be defined for each by:
- Then is a homomorphism from to since for all we have by the laws of exponents that:
- Let and suppose that . Then , so , so is injective.
- Furthermore, if then is such that , so is surjective.
- Thus is an isomorphism of to .
Theorem 2: If is a finite cyclic group of order then is isomorphic to .
- Proof: Suppose that . Then . Let be defined by:
- Then is a homomorphism since if is such that then:
- And if is such that then we can write where and (by the division algorithm) so that:
- It is easy to see that is injective and surjective, so is an isomorphism of and .
Proposition 3: Two finite cyclic groups and are isomorphic if and only if they are of the same order.
Proposition 4: If is a cyclic group and is a subgroup of then is also cyclic group. Furthermore, if is a finite cyclic group of order then for each with there exists a unique subgroup of with .
Proposition 5: Let be a finite cyclic group of order with . Then is generated by if and only if .
Subgroups of Cyclic Groups are Cyclic Groups
A group is said to be a cyclic group if for some , i.e., can be generated by a single element .
We will now prove an important theorem - every subgroup of a cyclic group is also cyclic.
Theorem 1: Let be a cyclic group. Then any subgroup of is also a cyclic group.
The converse of Theorem 1 is not true in general, i.e., even if every proper subgroup of a group is cyclic - it might be the case that is not cyclic. The simplest example of this is the group . The only proper subgroups of this group are the trivial group and - both of which are cyclic. But it is easy to check that is not cyclic.
- Proof: Let be a cyclic group. Then there exists an such that . Let be a subgroup of .
- If is the trivial subgroup, then clearly , and so is a cyclic group.
- If is not the trivial subgroup then there exists a such that . Since , there exists an such that , and . Since is itself a group and we have that with .
- So there exists an element with . Consider the set . This set is a nonempty subset of , and so by the Well-Ordering principle, it contains a least element, call it .
- Now since and is a group, we have that . S let . Since we have that . So for some . Using the division algorithm on and , we see that there exists integers such that:
- With . But then:
- Since and we see that:
- If , then . But , which contradicts the minimality of in . So we must have that . So:
- Thus , showing that . Thus we conclude that , i.e., is a cyclic group.
Licensing
Content obtained and/or adapted from:
- Cyclic group, Wikipedia under a CC BY-SA license
- Basic Theorems Regarding Cyclic Groups, mathonline.wikidot.com under a CC BY-SA license






























![{\displaystyle {\begin{aligned}\quad \varphi (a^{i})=[i]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5137e9c975cc3b8247522bf22f166dab0b0fdde9)


![{\displaystyle {\begin{aligned}\quad \varphi (a^{i}\cdot a^{j})=\varphi (a^{i+j})=[i]+[j]=\varphi (a^{i})+\varphi (a^{j})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6389b70bdec693019e0b21795cef72356d9b6016)




![{\displaystyle {\begin{aligned}\quad \varphi (a^{i}\cdot a^{j})=\varphi (a^{i+j})=\varphi (a^{qn+r})=\varphi ((a^{n})^{q}a^{r})=\varphi (1^{q}a^{r})=\varphi (a^{r})=[r]=[qn+r]=[i+j]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac8b42568323d060f5e2ff148f1161fd0b5e40b4)














































