Sequences:Limits

The sequence given by the perimeters of regular n-sided polygons that circumscribe the unit circle has a limit equal to the perimeter of the circle, i.e. $2\pi r.$ The corresponding sequence for inscribed polygons has the same limit.

n	n sin(1/n)
1	0.841471
2	0.958851
...
10	0.998334
...
100	0.999983

As the positive integer $n$ becomes larger and larger, the value $n\cdot \sin \left({\tfrac {1}{n}}\right)$ becomes arbitrarily close to $1.$ We say that "the limit of the sequence $n\cdot \sin \left({\tfrac {1}{n}}\right)$ equals $1.$"

In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to", and is often denoted using the $\lim$ symbol (e.g., $\lim _{n\to \infty }a_{n}$). If such a limit exists, the sequence is called convergent. A sequence that does not converge is said to be divergent. The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests.

Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers.

Real numbers

The plot of a convergent sequence {a_n} is shown in blue. Here, one can see that the sequence is converging to the limit 0 as n increases.

In the real numbers, a number $L$ is the limit of the sequence $(x_{n}),$ if the numbers in the sequence become closer and closer to $L$—and not to any other number.

Examples

• If $x_{n}=c$ for constant c, then $x_{n}\to c.$

• If $x_{n}={\frac {1}{n}},$ then $x_{n}\to 0.$

• If $x_{n}=1/n$ when $n$ is even, and $x_{n}={\frac {1}{n^{2}}}$ when $n$ is odd, then $x_{n}\to 0.$ (The fact that $x_{n+1}>x_{n}$ whenever $n$ is odd is irrelevant.)

• Given any real number, one may easily construct a sequence that converges to that number by taking decimal approximations. For example, the sequence $0.3,0.33,0.333,0.3333,\dots$ converges to $1/3.$ Note that the decimal representation $0.3333...$ is the limit of the previous sequence, defined by
  $$0.3333...:=\lim _{n\to \infty }\sum _{i=1}^{n}{\frac {3}{10^{i}}}.$$
• Finding the limit of a sequence is not always obvious. Two examples are $\lim _{n\to \infty }\left(1+{\tfrac {1}{n}}\right)^{n}$ (the limit of which is the number e) and the Arithmetic–geometric mean. The squeeze theorem is often useful in the establishment of such limits.

Formal definition

We call $x$ the limit of the sequence $(x_{n})$ if the following condition holds:

• For each real number $\varepsilon >0,$ there exists a natural number $N$ such that, for every natural number $n\geq N,$ we have $|x_{n}-x|<\varepsilon .$

In other words, for every measure of closeness $\varepsilon ,$ the sequence's terms are eventually that close to the limit. The sequence $(x_{n})$ is said to converge to or tend to the limit $x,$ written $x_{n}\to x$ or $\lim _{n\to \infty }x_{n}=x.$

Symbolically, this is:

$$\forall \varepsilon >0\left(\exists N\in \mathbb {N} \left(\forall n\in \mathbb {N} \left(n\geq N\implies |x_{n}-x|<\varepsilon \right)\right)\right).$$

If a sequence $(x_{n})$ converges to some limit $x,$ then it is convergent and $x$ is the only limit; otherwise $(x_{n})$ is divergent. A sequence that has zero as its limit is sometimes called a null sequence.

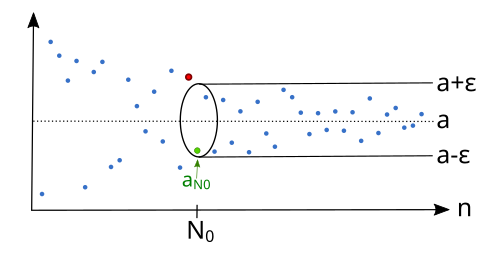
Illustration

• 

  Example of a sequence which converges to the limit $a.$

• 

  Regardless which $\varepsilon >0$ we have, there is an index $N_{0},$ so that the sequence lies afterwards completely in the epsilon tube $(a-\varepsilon ,a+\varepsilon ).$

• 

  There is also for a smaller $\epsilon _{1}>0$ an index $N_{1},$ so that the sequence is afterwards inside the epsilon tube $(a-\varepsilon _{1},a+\varepsilon _{1}).$

• 

  For each $\varepsilon >0$ there are only finitely many sequence members outside the epsilon tube.

Properties

Limits of sequences behave well with respect to the usual arithmetic operations. If $a_{n}\to a$ and $b_{n}\to b,$ then $a_{n}+b_{n}\to a+b,$ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n\cdot b_n \to ab} and, if neither b nor any Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_n} is zero, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_n}{b_n} \to \frac{a}{b}.}

For any continuous function f, if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n \to x} then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_n) \to f(x).} In fact, any real-valued function f is continuous if and only if it preserves the limits of sequences (though this is not necessarily true when using more general notions of continuity).

Some other important properties of limits of real sequences include the following (provided, in each equation below, that the limits on the right exist).

• The limit of a sequence is unique.
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} (a_n \pm b_n) = \lim_{n\to\infty} a_n \pm \lim_{n\to\infty} b_n}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} c a_n = c \cdot \lim_{n\to\infty} a_n}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} (a_n \cdot b_n) = (\lim_{n\to\infty} a_n)\cdot( \lim_{n\to\infty} b_n)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} \left(\frac{a_n}{b_n}\right) = \frac{\lim\limits_{n\to\infty} a_n}{\lim\limits_{n\to\infty} b_n}} provided Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} b_n \ne 0}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} a_n^p = \left[ \lim_{n\to\infty} a_n \right]^p}
• If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n \leq b_n} for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} greater than some Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N,} then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} a_n \leq \lim_{n\to\infty} b_n .}
• (Squeeze theorem) If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n \leq c_n \leq b_n} for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n > N,} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} a_n = \lim_{n\to\infty} b_n = L,} then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty} c_n = L.}
• If a sequence is bounded and monotonic, then it is convergent.
• A sequence is convergent if and only if every subsequence is convergent.
• If every subsequence of a sequence has its own subsequence which converges to the same point, then the original sequence converges to that point.

These properties are extensively used to prove limits, without the need to directly use the cumbersome formal definition. For example. once it is proven that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/n \to 0,} it becomes easy to show—using the properties above—that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a}{b+\frac{c}{n}} \to \frac{a}{b}} (assuming that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \ne 0} ).

Infinite limits

A sequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_n)} is said to tend to infinity, written Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n \to \infty} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty}x_n = \infty,} if for every K, there is an N such that for every Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \geq N,} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n > K} ; that is, the sequence terms are eventually larger than any fixed K.

Similarly, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n \to -\infty} if for every K, there is an N such that for every Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \geq N,} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n < K.} If a sequence tends to infinity or minus infinity, then it is divergent. However, a divergent sequence need not tend to plus or minus infinity, and the sequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n=(-1)^n} provides one such example.

Metric spaces

Definition

A point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} of the metric space Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X, d)} is the limit of the sequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_n)} if for all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon > 0,} there is an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} such that, for every Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \geq N,} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d(x_n, x) < \epsilon.} This coincides with the definition given for real numbers when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X = \R} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d(x, y) = |x-y|.}

Properties

For any continuous function f, if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n \to x} then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_n) \to f(x).} In fact, a function f is continuous if and only if it preserves the limits of sequences.

Limits of sequences are unique when they exist, as distinct points are separated by some positive distance, so for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} less than half this distance, sequence terms cannot be within a distance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} of both points.

Topological spaces

Definition

A point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in X} of the topological space Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X, \tau)} is a limit or limit point of the sequence $\left(x_{n}\right)_{n\in \mathbb {N} }$ if for every neighborhood Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,} there exists some Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \in \N} such that for every Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \geq N,} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n \in U.} This coincides with the definition given for metric spaces, if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X, d)} is a metric space and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} is the topology generated by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d.}

A limit of a sequence of points Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(x_n\right)_{n \in \N}} in a topological space Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} is a special case of a limit of a function: the domain is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \N} in the space Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \N \cup \lbrace + \infty \rbrace,} with the induced topology of the affinely extended real number system, the range is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T,} and the function argument Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} tends to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\infty,} which in this space is a limit point of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \N.}

Properties

In a Hausdorff space, limits of sequences are unique whenever they exist. Note that this need not be the case in non-Hausdorff spaces; in particular, if two points Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are topologically indistinguishable, then any sequence that converges to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} must converge to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} and vice versa.

Licensing

Content obtained and/or adapted from:

• Limit of a sequence, Wikipedia under a CC BY-SA license