Definition of Supremum and Infimum
Definition: Let  be a set that is bounded above. We say that the supremum of
be a set that is bounded above. We say that the supremum of  denoted
denoted  is a number
is a number  that satisfies the conditions that
that satisfies the conditions that  is an upper bound of
is an upper bound of  and
and  is the least upper bound of
is the least upper bound of  , that is for any
, that is for any  that is also an upper bound of
that is also an upper bound of  then
then  .
.
Definition: Let  be a set that is bounded below. We say that the infimum of
be a set that is bounded below. We say that the infimum of  denoted
denoted  is a number
is a number  that satisfies the conditions that
that satisfies the conditions that  is a lower bound of
is a lower bound of  and
and  is the greatest lower bound of
is the greatest lower bound of  , that is for any
, that is for any  that is also a lower bound of
that is also a lower bound of  then
then  .
.
We will now reformulate these definitions with an equivalent statement that may be useful to apply in certain situations in showing that an upper bound  is the supremum of a set, or showing that a lower bound
is the supremum of a set, or showing that a lower bound  is the infimum of a set.
is the infimum of a set.
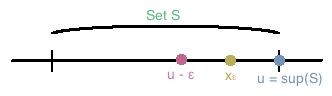
Theorem 1: Let  be a nonempty subset of the real numbers that is bounded above. The upper bound
be a nonempty subset of the real numbers that is bounded above. The upper bound  is said to be the supremum of
is said to be the supremum of  if and only if
if and only if  there exists an element
there exists an element  such that
such that  .
.
- Proof:
 Let
Let  be a nonempty subset of the real numbers that is bounded above. We first want to show that if
be a nonempty subset of the real numbers that is bounded above. We first want to show that if  is an upper bound such that
is an upper bound such that  there exists an element
there exists an element  such that
such that  , then
, then  . Let
. Let  be an upper bound of
be an upper bound of  that satisfies the condition stated above, and suppose that
that satisfies the condition stated above, and suppose that  . Then choose
. Then choose  , and so
, and so  and so there exists an element
and so there exists an element  such that
such that  , and thus,
, and thus,  .
.
 We now want to show that if
We now want to show that if  then
then  there exists an element
there exists an element  such that
such that  . Let
. Let  and let
and let  . We note that
. We note that  and so
and so  is not an upper bound of the set
is not an upper bound of the set  . Therefore by the definition that
. Therefore by the definition that  , there exists some element
, there exists some element  such that
such that  .
. 
Theorem 2: Let  be a nonempty subset of the real numbers that is bounded below. The lower bound
be a nonempty subset of the real numbers that is bounded below. The lower bound  is said to be the infimum of
is said to be the infimum of  if and only if
if and only if  there exists an element
there exists an element  such that
such that  .
.
- Proof:
 Let
Let  be a nonempty subset of the real numbers that is bounded below. We first want to show that if
be a nonempty subset of the real numbers that is bounded below. We first want to show that if  is a lower bound such that
is a lower bound such that  there exists an element
there exists an element  such that
such that  , then
, then  . Let
. Let  be a lower bound of
be a lower bound of  that satisfies the condition stated above, and suppose that
that satisfies the condition stated above, and suppose that  . Then choose
. Then choose  , and so
, and so  and so there exists an element
and so there exists an element  such that
such that  , and thus,
, and thus,  .
.
 We now want to show that if
We now want to show that if  then
then  there exists an element
there exists an element  such that
such that  . Let
. Let  and let
and let  . We note that
. We note that  and so
and so  is not a lower bound of the set
is not a lower bound of the set  . Therefore by the definition that
. Therefore by the definition that  , there exists some element
, there exists some element  such that
such that  .
. 
The Supremum and Infimum of a Function
We will now begin to look at some applications of the definition of a supremum and infimum with regards to functions.
Definition: Let  be a function. Then define the supremum of
be a function. Then define the supremum of  to be
to be  , and define the infimum of
, and define the infimum of  to be
to be  where
where  is the range of
is the range of  .
.
From the definition above, we acknowledge that the supremum and infimum of a function  pertain to the set
pertain to the set  that is the range of
that is the range of  . The diagram below illustrates the supremum and infimum of a function:
. The diagram below illustrates the supremum and infimum of a function:
We will now look at some important theorems.
Theorem 1: Let  and
and  be functions such that
be functions such that  is bounded above. If
is bounded above. If  for all
for all  , then
, then  .
.
- Proof: Let
 . Let
. Let  be a function that is bounded above. Since the range of
be a function that is bounded above. Since the range of  is nonempty we have that for all
is nonempty we have that for all  ,
,  . Now since
. Now since  for all
for all  , we have that
, we have that  .
.
- Furthermore we note that since
 for all
for all  , then
, then  is bounded below by
is bounded below by  , and so
, and so  and thus
and thus  .
. 
Theorem 2: Let  and
and  be functions such that
be functions such that  is bounded below. If
is bounded below. If  for all
for all  , then
, then  .
.
- Proof: Let
 be a function that is bounded below. Let
be a function that is bounded below. Let  . Since the range of
. Since the range of  is nonempty we have that for all
is nonempty we have that for all  ,
,  . Now since
. Now since  for all
for all  we have that
we have that  .
.
- Furthermore we note that since
 for all
for all  , then
, then  is bounded above by
is bounded above by  , and so
, and so  and thus
and thus  .
. 
Theorem 3: Let  be a bounded function and let
be a bounded function and let  . If
. If  then
then  , and
, and  . If
. If  then
then  , and
, and  .
.
Theorem 3 immediately follows from the theorems we've already proven on <a href="/the-supremum-and-infimum-of-the-bounded-set-as">The Supremum and Infimum of The Bounded Set (aS)</a> page where  .
.
The Completeness Property of The Real Numbers
We will now look at yet again another crucially important property of the real numbers which will allow us to call the set of  numbers under the operations of addition and multiplication a complete ordered field. This property will ensure that there is no "gaps" in the real number line, that is the real number line is continuous. The property is as follows.
numbers under the operations of addition and multiplication a complete ordered field. This property will ensure that there is no "gaps" in the real number line, that is the real number line is continuous. The property is as follows.
The Completeness Property of The Real Numbers: Every nonempty subset  of the real numbers that is bounded above has a supremum in
of the real numbers that is bounded above has a supremum in  .
.
The Completeness Property is also often called the "Least Upper Bound Property".
The completeness property above is a crucial axiom. A similar theorem regarding nonempty subsets  of the real numbers that are bounded below exists and is proven below.
of the real numbers that are bounded below exists and is proven below.
Theorem 1: Every nonempty subset  of the real numbers that is bounded below has an infimum in
of the real numbers that is bounded below has an infimum in  .
.
- Proof: Let
 be a nonempty subset of real numbers that is bounded below. Then there exists a lower bound
be a nonempty subset of real numbers that is bounded below. Then there exists a lower bound  such that
such that  for every
for every  .
.
- Define the set
 by:
by:

- Then observe that
 for every
for every  . So
. So  is a nonempty subset of real numbers that is bounded above. By the completeness property of the real numbers we have that
is a nonempty subset of real numbers that is bounded above. By the completeness property of the real numbers we have that  has a supremum in
has a supremum in  . Let
. Let  . Then
. Then  for every
for every  and if
and if  is any other upper bound of
is any other upper bound of  then
then  .
.
- So observe that
 for every
for every  and if
and if  is any other lower bound of
is any other lower bound of  then
then  . So
. So  . In other words,
. In other words,  has an infimum in
has an infimum in  .
. 
Licensing
Content obtained and/or adapted from: