Difference between revisions of "The Cartiesian Product"
(Created page with "File:Cartesian Product qtl1.svg|thumb|Cartesian product <math>\scriptstyle A \times B</math> of the sets <math>\scriptstyle A=\{x,y,z\}</math> and <math>\scriptstyle B=\{1,2...") |
|||
| Line 96: | Line 96: | ||
: <math>(A \times B)^\complement = \left(A^\complement \times B^\complement\right) \cup \left(A^\complement \times B\right) \cup \left(A \times B^\complement\right)\!,</math><ref name="planetmath"/> | : <math>(A \times B)^\complement = \left(A^\complement \times B^\complement\right) \cup \left(A^\complement \times B\right) \cup \left(A \times B^\complement\right)\!,</math><ref name="planetmath"/> | ||
| − | where <math>A^\complement</math> denotes the | + | where <math>A^\complement</math> denotes the absolute complement of ''A''. |
| − | Other properties related with | + | Other properties related with subsets are: |
:<math>\text{if } A \subseteq B \text{, then } A \times C \subseteq B \times C;</math> | :<math>\text{if } A \subseteq B \text{, then } A \times C \subseteq B \times C;</math> | ||
:<math>\text{if both } A,B \neq \emptyset \text{, then } A \times B \subseteq C \times D \!\iff\! A \subseteq C \text{ and } B \subseteq D.</math><ref>Cartesian Product of Subsets. (February 15, 2011). ''ProofWiki''. Retrieved 05:06, August 1, 2011 from https://proofwiki.org/w/index.php?title=Cartesian_Product_of_Subsets&oldid=45868</ref><!-- Better replace citation with a non-wiki site. --> | :<math>\text{if both } A,B \neq \emptyset \text{, then } A \times B \subseteq C \times D \!\iff\! A \subseteq C \text{ and } B \subseteq D.</math><ref>Cartesian Product of Subsets. (February 15, 2011). ''ProofWiki''. Retrieved 05:06, August 1, 2011 from https://proofwiki.org/w/index.php?title=Cartesian_Product_of_Subsets&oldid=45868</ref><!-- Better replace citation with a non-wiki site. --> | ||
| Line 105: | Line 105: | ||
{{See also|Cardinal arithmetic}} | {{See also|Cardinal arithmetic}} | ||
| − | The | + | The cardinality of a set is the number of elements of the set. For example, defining two sets: {{nowrap|1=''A'' = {a, b} }} and {{nowrap|1=''B'' = {5, 6}.}} Both set ''A'' and set ''B'' consist of two elements each. Their Cartesian product, written as {{nowrap|''A'' × ''B''}}, results in a new set which has the following elements: |
: ''A'' × ''B'' = {(a,5), (a,6), (b,5), (b,6)}. | : ''A'' × ''B'' = {(a,5), (a,6), (b,5), (b,6)}. | ||
| Line 118: | Line 118: | ||
and so on. | and so on. | ||
| − | The set {{nowrap|''A'' × ''B''}} is | + | The set {{nowrap|''A'' × ''B''}} is infinite if either ''A'' or ''B'' is infinite, and the other set is not the empty set.<ref>Peter S. (1998). A Crash Course in the Mathematics of Infinite Sets. ''St. John's Review, 44''(2), 35–59. Retrieved August 1, 2011, from http://www.mathpath.org/concepts/infinity.htm</ref> |
== Cartesian products of several sets == | == Cartesian products of several sets == | ||
| Line 127: | Line 127: | ||
: <math>X_1\times\cdots\times X_n = \{(x_1, \ldots, x_n) \mid x_i \in X_i \ \text{for every} \ i \in \{1, \ldots, n\} \}</math> | : <math>X_1\times\cdots\times X_n = \{(x_1, \ldots, x_n) \mid x_i \in X_i \ \text{for every} \ i \in \{1, \ldots, n\} \}</math> | ||
| − | of | + | of ''n''-tuples. If tuples are defined as nested ordered pairs, it can be identified with {{nowrap|(''X''<sub>1</sub> × ⋯ × ''X''<sub>''n''−1</sub>) × ''X<sub>n</sub>''}}. If a tuple is defined as a function on {{nowrap|{1, 2, …, ''n''} }} that takes its value at ''i'' to be the ''i''th element of the tuple, then the Cartesian product ''X''<sub>1</sub>×⋯×''X''<sub>''n''</sub> is the set of functions |
: <math>\{ x:\{1,\ldots,n\}\to X_1\cup\cdots\cup X_n \ | \ x(i)\in X_i \ \text{for every} \ i \in \{1, \ldots, n\} \}.</math> | : <math>\{ x:\{1,\ldots,n\}\to X_1\cup\cdots\cup X_n \ | \ x(i)\in X_i \ \text{for every} \ i \in \{1, \ldots, n\} \}.</math> | ||
| Line 133: | Line 133: | ||
=== ''n''-ary Cartesian power === | === ''n''-ary Cartesian power === | ||
The '''Cartesian square''' of a set ''X'' is the Cartesian product {{nowrap|1=''X''<sup>2</sup> = ''X'' × ''X''}}. | The '''Cartesian square''' of a set ''X'' is the Cartesian product {{nowrap|1=''X''<sup>2</sup> = ''X'' × ''X''}}. | ||
| − | An example is the 2-dimensional | + | An example is the 2-dimensional plane {{nowrap|1='''R'''<sup>2</sup> = '''R''' × '''R'''}} where '''R''' is the set of real numbers:<ref name=":1" /> '''R'''<sup>2</sup> is the set of all points {{nowrap|(''x'',''y'')}} where ''x'' and ''y'' are real numbers. |
The ''' ''n''-ary Cartesian power''' of a set ''X'', denoted <math>X^n</math>, can be defined as | The ''' ''n''-ary Cartesian power''' of a set ''X'', denoted <math>X^n</math>, can be defined as | ||
| Line 141: | Line 141: | ||
An example of this is {{nowrap|1='''R'''<sup>3</sup> = '''R''' × '''R''' × '''R'''}}, with '''R''' again the set of real numbers,<ref name=":1" /> and more generally '''R'''<sup>''n''</sup>. | An example of this is {{nowrap|1='''R'''<sup>3</sup> = '''R''' × '''R''' × '''R'''}}, with '''R''' again the set of real numbers,<ref name=":1" /> and more generally '''R'''<sup>''n''</sup>. | ||
| − | The ''n''-ary Cartesian power of a set ''X'' is | + | The ''n''-ary Cartesian power of a set ''X'' is isomorphic to the space of functions from an ''n''-element set to ''X''. As a special case, the 0-ary Cartesian power of ''X'' may be taken to be a singleton set, corresponding to the empty function with codomain ''X''. |
=== Infinite Cartesian products === | === Infinite Cartesian products === | ||
| − | It is possible to define the Cartesian product of an arbitrary (possibly | + | It is possible to define the Cartesian product of an arbitrary (possibly infinite) indexed family of sets. If ''I'' is any index set, and <math>\{X_i\}_{i\in I}</math> is a family of sets indexed by ''I'', then the Cartesian product of the sets in <math>\{X_i\}_{i\in I}</math> is defined to be |
: <math>\prod_{i \in I} X_i = \left\{\left. f: I \to \bigcup_{i \in I} X_i\ \right|\ (\forall i)(f(i) \in X_i)\right\},</math> | : <math>\prod_{i \in I} X_i = \left\{\left. f: I \to \bigcup_{i \in I} X_i\ \right|\ (\forall i)(f(i) \in X_i)\right\},</math> | ||
| − | that is, the set of all functions defined on the | + | that is, the set of all functions defined on the index set such that the value of the function at a particular index ''i'' is an element of ''X<sub>i</sub>''. Even if each of the ''X<sub>i</sub>'' is nonempty, the Cartesian product may be empty if the axiom of choice, which is equivalent to the statement that every such product is nonempty, is not assumed. |
For each ''j'' in ''I'', the function | For each ''j'' in ''I'', the function | ||
: <math> \pi_{j}: \prod_{i \in I} X_i \to X_{j},</math> | : <math> \pi_{j}: \prod_{i \in I} X_i \to X_{j},</math> | ||
| − | defined by <math>\pi_{j}(f) = f(j)</math> is called the '''''j''th | + | defined by <math>\pi_{j}(f) = f(j)</math> is called the '''''j''th projection map'''. |
'''Cartesian power''' is a Cartesian product where all the factors ''X<sub>i</sub>'' are the same set ''X''. In this case, | '''Cartesian power''' is a Cartesian product where all the factors ''X<sub>i</sub>'' are the same set ''X''. In this case, | ||
: <math>\prod_{i \in I} X_i = \prod_{i \in I} X</math> | : <math>\prod_{i \in I} X_i = \prod_{i \in I} X</math> | ||
| − | is the set of all functions from ''I'' to ''X'', and is frequently denoted ''X<sup>I</sup>''. This case is important in the study of | + | is the set of all functions from ''I'' to ''X'', and is frequently denoted ''X<sup>I</sup>''. This case is important in the study of cardinal exponentiation. An important special case is when the index set is <math>\mathbb{N}</math>, the natural numbers: this Cartesian product is the set of all infinite sequences with the ''i''th term in its corresponding set ''X<sub>i</sub>''. For example, each element of |
: <math>\prod_{n = 1}^\infty \mathbb R = \mathbb R \times \mathbb R \times \cdots</math> | : <math>\prod_{n = 1}^\infty \mathbb R = \mathbb R \times \mathbb R \times \cdots</math> | ||
| − | can be visualized as a | + | can be visualized as a vector with countably infinite real number components. This set is frequently denoted <math>\mathbb{R}^\omega</math>, or <math>\mathbb{R}^{\mathbb{N}}</math>. |
== Other forms == | == Other forms == | ||
| Line 169: | Line 169: | ||
: <math>(f\times g)(a, x) = (f(a), g(x)).</math> | : <math>(f\times g)(a, x) = (f(a), g(x)).</math> | ||
| − | This can be extended to | + | This can be extended to tuples and infinite collections of functions. |
This is different from the standard Cartesian product of functions considered as sets. | This is different from the standard Cartesian product of functions considered as sets. | ||
| Line 175: | Line 175: | ||
Let <math>A</math> be a set and <math>B \subseteq A</math>. Then the ''cylinder'' of <math>B</math> with respect to <math>A</math> is the Cartesian product <math>B \times A</math> of <math>B</math> and <math>A</math>. | Let <math>A</math> be a set and <math>B \subseteq A</math>. Then the ''cylinder'' of <math>B</math> with respect to <math>A</math> is the Cartesian product <math>B \times A</math> of <math>B</math> and <math>A</math>. | ||
| − | Normally, <math>A</math> is considered to be the | + | Normally, <math>A</math> is considered to be the universe of the context and is left away. For example, if <math>B</math> is a subset of the natural numbers <math>\mathbb{N}</math>, then the cylinder of <math>B</math> is <math>B \times \mathbb{N}</math>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 13:36, 9 November 2021
The Cartesian product of two sets A and B, denoted ATemplate:Hair space×Template:Hair spaceB, is the set of all ordered pairs Template:Nowrap where a is in A and b is in B. In terms of set-builder notation, that is
A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product Template:Nowrap is taken, the cells of the table contain ordered pairs of the form Template:Nowrap.
One can similarly define the Cartesian product of n sets, also known as an n-fold Cartesian product, which can be represented by an n-dimensional array, where each element is an n-tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets.
The Cartesian product is named after René Descartes, whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product.
Contents
Examples
A deck of cards
An illustrative example is the standard 52-card deck. The standard playing card ranks {A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2} form a 13-element set. The card suits Template:Nowrap form a four-element set. The Cartesian product of these sets returns a 52-element set consisting of 52 ordered pairs, which correspond to all 52 possible playing cards.
Template:Nowrap returns a set of the form {(A, ♠), (A, Template:Color), (A, Template:Color), (A, ♣), (K, ♠), …, (3, ♣), (2, ♠), (2, Template:Color), (2, Template:Color), (2, ♣)}.
Template:Nowrap returns a set of the form {(♠, A), (♠, K), (♠, Q), (♠, J), (♠, 10), …, (♣, 6), (♣, 5), (♣, 4), (♣, 3), (♣, 2)}.
These two sets are distinct, even disjoint.
A two-dimensional coordinate system
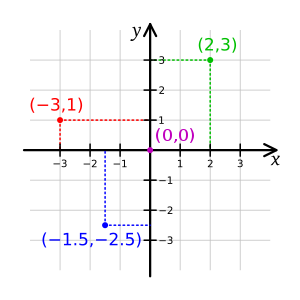
The main historical example is the Cartesian plane in analytic geometry. In order to represent geometrical shapes in a numerical way, and extract numerical information from shapes' numerical representations, René Descartes assigned to each point in the plane a pair of real numbers, called its coordinates. Usually, such a pair's first and second components are called its x and y coordinates, respectively (see picture). The set of all such pairs (i.e., the Cartesian product Template:Nowrap, with ℝ denoting the real numbers) is thus assigned to the set of all points in the plane.Template:Cn
Most common implementation (set theory)
A formal definition of the Cartesian product from set-theoretical principles follows from a definition of ordered pair. The most common definition of ordered pairs, Kuratowski's definition, is . Under this definition, is an element of , and is a subset of that set, where represents the power set operator. Therefore, the existence of the Cartesian product of any two sets in ZFC follows from the axioms of pairing, union, power set, and specification. Since functions are usually defined as a special case of relations, and relations are usually defined as subsets of the Cartesian product, the definition of the two-set Cartesian product is necessarily prior to most other definitions.
Non-commutativity and non-associativity
Let A, B, C, and D be sets.
The Cartesian product Template:Nowrap is not commutative,
because the ordered pairs are reversed unless at least one of the following conditions is satisfied:
- A is equal to B, or
- A or B is the empty set.
For example:
- A = {1,2}; B = {3,4}
- A × B = {1,2} × {3,4} = {(1,3), (1,4), (2,3), (2,4)}
- B × A = {3,4} × {1,2} = {(3,1), (3,2), (4,1), (4,2)}
- A = B = {1,2}
- A × B = B × A = {1,2} × {1,2} = {(1,1), (1,2), (2,1), (2,2)}
- A = {1,2}; B = ∅
- A × B = {1,2} × ∅ = ∅
- B × A = ∅ × {1,2} = ∅
Strictly speaking, the Cartesian product is not associative (unless one of the involved sets is empty).
If for example A = {1}, then Template:Nowrap Template:Nowrap.
Intersections, unions, and subsets
Script error: No such module "Multiple_image". The Cartesian product satisfies the following property with respect to intersections (see middle picture).
In most cases, the above statement is not true if we replace intersection with union (see rightmost picture).
In fact, we have that:
For the set difference, we also have the following identity:
Here are some rules demonstrating distributivity with other operators (see leftmost picture):[2]
where denotes the absolute complement of A.
Other properties related with subsets are:
Cardinality
The cardinality of a set is the number of elements of the set. For example, defining two sets: Template:Nowrap and Template:Nowrap Both set A and set B consist of two elements each. Their Cartesian product, written as Template:Nowrap, results in a new set which has the following elements:
- A × B = {(a,5), (a,6), (b,5), (b,6)}.
where each element of A is paired with each element of B, and where each pair makes up one element of the output set. The number of values in each element of the resulting set is equal to the number of sets whose Cartesian product is being taken; 2 in this case. The cardinality of the output set is equal to the product of the cardinalities of all the input sets. That is,
- |A × B| = |A| · |B|.[1]
In this case, |A × B| = 4
Similarly
- |A × B × C| = |A| · |B| · |C|
and so on.
The set Template:Nowrap is infinite if either A or B is infinite, and the other set is not the empty set.[5]
Cartesian products of several sets
n-ary Cartesian product
The Cartesian product can be generalized to the n-ary Cartesian product over n sets X1, ..., Xn as the set
of n-tuples. If tuples are defined as nested ordered pairs, it can be identified with Template:Nowrap. If a tuple is defined as a function on Template:Nowrap that takes its value at i to be the ith element of the tuple, then the Cartesian product X1×⋯×Xn is the set of functions
n-ary Cartesian power
The Cartesian square of a set X is the Cartesian product Template:Nowrap. An example is the 2-dimensional plane Template:Nowrap where R is the set of real numbers:[6] R2 is the set of all points Template:Nowrap where x and y are real numbers.
The n-ary Cartesian power of a set X, denoted , can be defined as
An example of this is Template:Nowrap, with R again the set of real numbers,[6] and more generally Rn.
The n-ary Cartesian power of a set X is isomorphic to the space of functions from an n-element set to X. As a special case, the 0-ary Cartesian power of X may be taken to be a singleton set, corresponding to the empty function with codomain X.
Infinite Cartesian products
It is possible to define the Cartesian product of an arbitrary (possibly infinite) indexed family of sets. If I is any index set, and is a family of sets indexed by I, then the Cartesian product of the sets in is defined to be
that is, the set of all functions defined on the index set such that the value of the function at a particular index i is an element of Xi. Even if each of the Xi is nonempty, the Cartesian product may be empty if the axiom of choice, which is equivalent to the statement that every such product is nonempty, is not assumed.
For each j in I, the function
defined by is called the jth projection map.
Cartesian power is a Cartesian product where all the factors Xi are the same set X. In this case,
is the set of all functions from I to X, and is frequently denoted XI. This case is important in the study of cardinal exponentiation. An important special case is when the index set is , the natural numbers: this Cartesian product is the set of all infinite sequences with the ith term in its corresponding set Xi. For example, each element of
can be visualized as a vector with countably infinite real number components. This set is frequently denoted , or .
Other forms
Abbreviated form
If several sets are being multiplied together (e.g., X1, X2, X3, …), then some authors[7] choose to abbreviate the Cartesian product as simply ×Xi.
Cartesian product of functions
If f is a function from A to B and g is a function from X to Y, then their Cartesian product Template:Nowrap is a function from Template:Nowrap to Template:Nowrap with
This can be extended to tuples and infinite collections of functions. This is different from the standard Cartesian product of functions considered as sets.
Cylinder
Let be a set and . Then the cylinder of with respect to is the Cartesian product of and .
Normally, is considered to be the universe of the context and is left away. For example, if is a subset of the natural numbers , then the cylinder of is .
- ↑ 1.0 1.1 Cite error: Invalid
<ref>tag; no text was provided for refs named:2 - ↑ Singh, S. (August 27, 2009). Cartesian product. Retrieved from the Connexions Web site: http://cnx.org/content/m15207/1.5/
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedplanetmath - ↑ Cartesian Product of Subsets. (February 15, 2011). ProofWiki. Retrieved 05:06, August 1, 2011 from https://proofwiki.org/w/index.php?title=Cartesian_Product_of_Subsets&oldid=45868
- ↑ Peter S. (1998). A Crash Course in the Mathematics of Infinite Sets. St. John's Review, 44(2), 35–59. Retrieved August 1, 2011, from http://www.mathpath.org/concepts/infinity.htm
- ↑ 6.0 6.1 Cite error: Invalid
<ref>tag; no text was provided for refs named:1 - ↑ Osborne, M., and Rubinstein, A., 1994. A Course in Game Theory. MIT Press.















![{\displaystyle (A\times C)\cup (B\times D)=[(A\setminus B)\times C]\cup [(A\cap B)\times (C\cup D)]\cup [(B\setminus A)\times D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67cfa315894265914c23ed2d555d05e6255d98a4)
![{\displaystyle (A\times C)\setminus (B\times D)=[A\times (C\setminus D)]\cup [(A\setminus B)\times C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/401c029889c8cdaaa16d20a38c311158b98cfd41)























