Difference between revisions of "The Law of Cosines"
Rylee.taylor (talk | contribs) (fixing link to go straight to pdf) |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Law of Cosines== | ||
| + | [[Image:Law-of-cosines1.svg]] | ||
| + | |||
| + | The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines: | ||
| + | |||
| + | :<math>a^2+b^2-2ab\cos(\theta)=c^2</math> | ||
| + | where <math>\theta</math> is the angle between sides <math>a</math> and <math>b</math> . | ||
| + | |||
| + | ===Does the formula make sense?=== | ||
| + | This formula had better agree with the Pythagorean Theorem when <math>\theta=90^\circ</math> . | ||
| + | |||
| + | So try it... | ||
| + | |||
| + | When <math>\theta=90^\circ</math> , <math>\cos(\theta)=\cos(90^\circ)=0</math> | ||
| + | |||
| + | The <math>-2ab\cos(\theta)=0</math> and the formula reduces to the usual Pythagorean theorem. | ||
| + | |||
| + | ==Permutations== | ||
| + | For any triangle with angles <math>A,B,C</math> and corresponding opposite side lengths <math>a,b,c</math> , the Law of Cosines states that | ||
| + | :<math>a^2=b^2+c^2-2bc\cdot\cos(A)</math> | ||
| + | :<math>b^2=a^2+c^2-2ac\cdot\cos(B)</math> | ||
| + | :<math>c^2=a^2+b^2-2ab\cdot\cos(C)</math> | ||
| + | |||
| + | ===Proof=== | ||
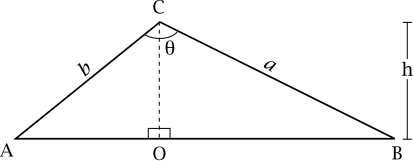
| + | [[Image:Law-of-cosines2.svg]] | ||
| + | |||
| + | Dropping a perpendicular <math>OC</math> from vertex <math>C</math> to intersect <math>AB</math> (or <math>AB</math> extended) at <math>O</math> splits this triangle into two right-angled triangles <math>AOC</math> and <math>BOC</math> , with altitude <math>h</math> from side <math>c</math> . | ||
| + | |||
| + | First we will find the lengths of the other two sides of triangle <math>AOC</math> in terms of known quantities, using triangle <math>BOC</math> . | ||
| + | |||
| + | :<math>h=a\sin(B)</math> | ||
| + | Side <math>c</math> is split into two segments, with total length <math>c</math> . | ||
| + | :<math>\overline{OB}</math> has length <math>\overline{BC}\cos(B)=a\cos(B)</math> | ||
| + | :<math>\overline{AO}=\overline{AB}-\overline{OB}</math> has length <math>c-a\cos(B)</math> | ||
| + | |||
| + | Now we can use the Pythagorean Theorem to find <math>b</math> , since <math>b^2=\overline{AO}^2+h^2</math> . | ||
| + | :{| | ||
| + | |<math>b^2</math> | ||
| + | |<math>=\bigl(c-a\cos(B)\bigr)^2+a^2\sin^2(B)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=c^2-2ac\cos(B)+a^2\cos^2(B)+a^2\sin^2(B)</math> | ||
| + | |- | ||
| + | | | ||
| + | |<math>=a^2+c^2-2ac\cos(B)</math> | ||
| + | |} | ||
| + | |||
| + | The corresponding expressions for <math>a</math> and <math>c</math> can be proved similarly. | ||
| + | |||
| + | The formula can be rearranged: | ||
| + | :<math>\cos(C)=\frac{a^2+b^2-c^2}{2ab}</math> | ||
| + | and similarly for <math>cos(A)</math> and <math>cos(B)</math> . | ||
| + | |||
| + | ==Applications== | ||
| + | This formula can be used to find the third side of a triangle if the other two sides and the angle between them are known. The rearranged formula can be used to find the angles of a triangle if all three sides are known. | ||
| + | |||
| + | |||
| + | ==Resources== | ||
* [https://mathresearch.utsa.edu/wikiFiles/MAT1093/The%20Law%20of%20Cosines/Esparza%201093%20Notes%204.3A.pdf The Law of Cosines]. Written notes created by Professor Esparza, UTSA. | * [https://mathresearch.utsa.edu/wikiFiles/MAT1093/The%20Law%20of%20Cosines/Esparza%201093%20Notes%204.3A.pdf The Law of Cosines]. Written notes created by Professor Esparza, UTSA. | ||
* [https://mathresearch.utsa.edu/wikiFiles/MAT1093/The%20Law%20of%20Cosines/Esparza%201093%20Notes%204.3B.pdf The Law of Cosines Continued]. Written notes created by Professor Esparza, UTSA. | * [https://mathresearch.utsa.edu/wikiFiles/MAT1093/The%20Law%20of%20Cosines/Esparza%201093%20Notes%204.3B.pdf The Law of Cosines Continued]. Written notes created by Professor Esparza, UTSA. | ||
| + | |||
| + | == Licensing == | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikibooks.org/wiki/Trigonometry/Law_of_Cosines Law of Cosines, Wikibooks] under a CC BY-SA license | ||
Latest revision as of 17:00, 28 October 2021
Contents
Law of Cosines
The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:
where is the angle between sides and .
Does the formula make sense?
This formula had better agree with the Pythagorean Theorem when .
So try it...
When ,
The and the formula reduces to the usual Pythagorean theorem.
Permutations
For any triangle with angles and corresponding opposite side lengths , the Law of Cosines states that
Proof
Dropping a perpendicular from vertex to intersect (or extended) at splits this triangle into two right-angled triangles and , with altitude from side .
First we will find the lengths of the other two sides of triangle in terms of known quantities, using triangle .
Side is split into two segments, with total length .
- has length
- has length
Now we can use the Pythagorean Theorem to find , since .
The corresponding expressions for and can be proved similarly.
The formula can be rearranged:
and similarly for and .
Applications
This formula can be used to find the third side of a triangle if the other two sides and the angle between them are known. The rearranged formula can be used to find the angles of a triangle if all three sides are known.
Resources
- The Law of Cosines. Written notes created by Professor Esparza, UTSA.
- The Law of Cosines Continued. Written notes created by Professor Esparza, UTSA.
Licensing
Content obtained and/or adapted from:
- Law of Cosines, Wikibooks under a CC BY-SA license