Difference between revisions of "The Topology of Higher Dimensions: interior, closure and boundary"
| Line 5: | Line 5: | ||
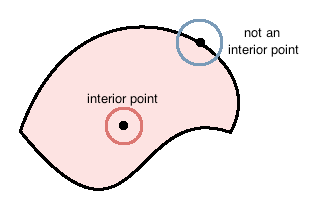
<p>In the case where <span class="math-inline"><math>n = 2</math></span> and we have some subset <span class="math-inline"><math>S \subseteq \mathbb{R}^2</math></span> (like the one illustrated below), then we say that a point <span class="math-inline"><math>\mathbf{a} \in \mathbb{R}^2</math></span> is an interior point if there exists an open disk of some positive radius <span class="math-inline"><math>r > 0</math></span> that is entirely contained in <span class="math-inline"><math>S</math></span>.</p> | <p>In the case where <span class="math-inline"><math>n = 2</math></span> and we have some subset <span class="math-inline"><math>S \subseteq \mathbb{R}^2</math></span> (like the one illustrated below), then we say that a point <span class="math-inline"><math>\mathbf{a} \in \mathbb{R}^2</math></span> is an interior point if there exists an open disk of some positive radius <span class="math-inline"><math>r > 0</math></span> that is entirely contained in <span class="math-inline"><math>S</math></span>.</p> | ||
| − | [[File:Interior point.png| | + | [[File:Interior point.png|center|Interior point]] |
<p>In the illustration above, we see that the point on the boundary of this subset is not an interior point. If we take a disk centered at this point of ANY positive radius then there will exist points in this disk that are always not contained within the pink region.</p> | <p>In the illustration above, we see that the point on the boundary of this subset is not an interior point. If we take a disk centered at this point of ANY positive radius then there will exist points in this disk that are always not contained within the pink region.</p> | ||
| Line 13: | Line 13: | ||
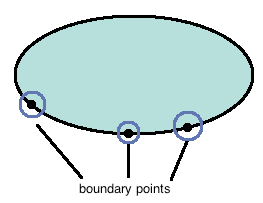
<p>For <span class="math-inline"><math>n = 1</math></span>, <span class="math-inline"><math>\mathrm{bdry} (S)</math></span> comprises the endpoints of <span class="math-inline"><math>S</math></span>. For <span class="math-inline"><math>n = 2</math></span>, <span class="math-inline"><math>\mathrm{bdry} (S)</math></span> comprises the border of <span class="math-inline"><math>S</math></span> as illustrated below:</p> | <p>For <span class="math-inline"><math>n = 1</math></span>, <span class="math-inline"><math>\mathrm{bdry} (S)</math></span> comprises the endpoints of <span class="math-inline"><math>S</math></span>. For <span class="math-inline"><math>n = 2</math></span>, <span class="math-inline"><math>\mathrm{bdry} (S)</math></span> comprises the border of <span class="math-inline"><math>S</math></span> as illustrated below:</p> | ||
| − | [[File:Boundary points.png| | + | [[File:Boundary points.png|center|Boundary points]] |
<p>For <span class="math-inline"><math>n = 3</math></span>, <span class="math-inline"><math>\mathrm{bdry} (S)</math></span> comprises the surface of <span class="math-inline"><math>S</math></span>.</p> | <p>For <span class="math-inline"><math>n = 3</math></span>, <span class="math-inline"><math>\mathrm{bdry} (S)</math></span> comprises the surface of <span class="math-inline"><math>S</math></span>.</p> | ||
| Line 21: | Line 21: | ||
<p>For <span class="math-inline"><math>n = 2</math></span>, a visualization of some exterior points of a set of points (in green) is illustrated below:</p> | <p>For <span class="math-inline"><math>n = 2</math></span>, a visualization of some exterior points of a set of points (in green) is illustrated below:</p> | ||
| − | [[File:Exterior points.png| | + | [[File:Exterior points.png|center|Exterior points]] |
Revision as of 14:31, 9 November 2021
We are now going to discuss some important classifications of points regarding a subset of which we define below.
Definition: Let . A point is said to be an Interior Point of if there exists an such that , i.e., there exists an open ball centered at for some positive radius that is a subset of . The set of all interior points of is denoted by .
In the case where and we have some subset (like the one illustrated below), then we say that a point is an interior point if there exists an open disk of some positive radius that is entirely contained in .
In the illustration above, we see that the point on the boundary of this subset is not an interior point. If we take a disk centered at this point of ANY positive radius then there will exist points in this disk that are always not contained within the pink region.
Definition: Let . A point is said to be a Boundary Point of if for every for every with there exists such that and , i.e., in every ball centered at there exists a point contained in and a point contained in the complement . The set of all boundary points of is denoted .
For , comprises the endpoints of . For , comprises the border of as illustrated below:
For , comprises the surface of .
Definition: Let . A point is said to be an Exterior Point of if . The set of all exterior points of is denoted .
For , a visualization of some exterior points of a set of points (in green) is illustrated below: