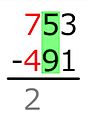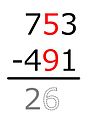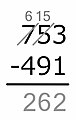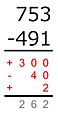Whole numbers subtraction models and properties
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, −. For example, in the adjacent picture, there are 5 − 2 peaches—meaning 5 peaches with 2 taken away, resulting in a total of 3 peaches. Therefore, the difference of 5 and 2 is 3; that is, 5 − 2 = 3. While primarily associated with natural numbers in arithmetic, subtraction can also represent removing or decreasing physical and abstract quantities using different kinds of objects including negative numbers, fractions, irrational numbers, vectors, decimals, functions, and matrices.
Subtraction follows several important patterns. It is anticommutative, meaning that changing the order changes the sign of the answer. It is also not associative, meaning that when one subtracts more than two numbers, the order in which subtraction is performed matters. Because 0 is the additive identity, subtraction of it does not change a number. Subtraction also obeys predictable rules concerning related operations, such as addition and multiplication. All of these rules can be proven, starting with the subtraction of integers and generalizing up through the real numbers and beyond. General binary operations that follow these patterns are studied in abstract algebra.
Performing subtraction on natural numbers is one of the simplest numerical tasks. Subtraction of very small numbers is accessible to young children. In primary education for instance, students are taught to subtract numbers in the decimal system, starting with single digits and progressively tackling more difficult problems.
In advanced algebra and in computer algebra, an expression involving subtraction like A − B is generally treated as a shorthand notation for the addition A + (−B). Thus, A − B contains two terms, namely A and −B. This allows an easier use of associativity and commutativity.
Notation and terminology
Subtraction is usually written using the minus sign "−" between the terms; that is, in infix notation. The result is expressed with an equals sign. For example,
- (pronounced as "two minus one equals one")
- (pronounced as "four minus two equals two")
- (pronounced as "six minus three equals three")
- (pronounced as "four minus six equals negative two")
There are also situations where subtraction is "understood", even though no symbol appears:
- A column of two numbers, with the lower number in red, usually indicates that the lower number in the column is to be subtracted, with the difference written below, under a line. This is most common in accounting.
Formally, the number being subtracted is known as the subtrahend, while the number it is subtracted from is the minuend. The result is the difference. That is,
- .
All of this terminology derives from Latin. "Subtraction" is an English word derived from the Latin verb subtrahere, which in turn is a compound of sub "from under" and trahere "to pull". Thus, to subtract is to draw from below, or to take away. Using the gerundive suffix -nd results in "subtrahend", "thing to be subtracted". Likewise, from minuere "to reduce or diminish", one gets "minuend", which means "thing to be diminished".
Properties
Anti-commutativity
Subtraction is anti-commutative, meaning that if one reverses the terms in a difference left-to-right, the result is the negative of the original result. Symbolically, if a and b are any two numbers, then
- a − b = −(b − a).
Non-associativity
Subtraction is non-associative, which comes up when one tries to define repeated subtraction. In general, the expression
- "a − b − c"
can be defined to mean either (a − b) − c or a − (b − c), but these two possibilities lead to different answers. To resolve this issue, one must establish an order of operations, with different orders yielding different results.
Predecessor
In the context of integers, subtraction of one also plays a special role: for any integer a, the integer (a − 1) is the largest integer less than a, also known as the predecessor of a.
Subtraction by hand
Austrian method
Example:
Subtraction from left to right
Example:
American method
In this method, each digit of the subtrahend is subtracted from the digit above it starting from right to left. If the top number is too small to subtract the bottom number from it, we add 10 to it; this 10 is "borrowed" from the top digit to the left, which we subtract 1 from. Then we move on to subtracting the next digit and borrowing as needed, until every digit has been subtracted. Example:
Trade first
A variant of the American method where all borrowing is done before all subtraction.
Example:
Partial differences
The partial differences method is different from other vertical subtraction methods because no borrowing or carrying takes place. In their place, one places plus or minus signs depending on whether the minuend is greater or smaller than the subtrahend. The sum of the partial differences is the total difference.
Example:
Nonvertical methods
Counting up
Instead of finding the difference digit by digit, one can count up the numbers between the subtrahend and the minuend.
Example: 1234 − 567 = can be found by the following steps:
- 567 + 3 = 570
- 570 + 30 = 600
- 600 + 400 = 1000
- 1000 + 234 = 1234
Add up the value from each step to get the total difference: 3 + 30 + 400 + 234 = 667.
Breaking up the subtraction
Another method that is useful for mental arithmetic is to split up the subtraction into small steps.
Example: 1234 − 567 = can be solved in the following way:
- 1234 − 500 = 734
- 734 − 60 = 674
- 674 − 7 = 667
Same change
The same change method uses the fact that adding or subtracting the same number from the minuend and subtrahend does not change the answer. One simply adds the amount needed to get zeros in the subtrahend.
Example:
"1234 − 567 =" can be solved as follows:
- 1234 − 567 = 1237 − 570 = 1267 − 600 = 667
Licensing
Content obtained and/or adapted from:
- Subtraction, Wikipedia under a CC BY-SA license