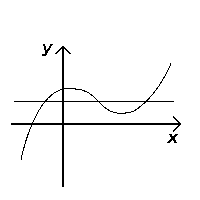One-to-one functions

$A$ is the domain of the function while $B$ is the range. This transformation from set $A$ to $B$ is an example of one-to-one function.

To make it simple, for the function $f(x)$, all of the possible $x$ values constitute the domain, and all of the values $f(x)$ ($y$ on the x-y plane) constitute the range. To put it in more formal terms, a function $f$ is a mapping of some element $a\in A$, called the domain, to exactly one element $b\in B$, called the range, such that $f:A\to B$. The image below should help explain the modern definition of a function:

A function is considered one-to-one if an element $a\in A$ from domain $A$ of function $f$, leads to exactly one element $b\in B$ from range $B$ of the function. By definition, since only one element $b$ is mapped by function $f$ from some element $a$, $f:A\to B$ implies that there exists only one element $b$ from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to Figure 1.

The horizontal line and the algebraic 1-1 test

Similarly, the horizontal line test, though does not test if an equation is a function, tests if a function is injective (one-to-one). If any horizontal line ever touches the graph at more than one point, then the function is not one-to-one; if the line always touches at most one point on the graph, then the function is one-to-one.

A one-to-one function passes the horizontal line test

This function does NOT pass the horiontal line test

The algebraic 1-1 test is the non-geometric way to see if a function is one-to-one. The basic concept is that:

Assume there is a function $f$. If:

$f(a)=f(b)$, and $a=b$, then

function $f$ is one-to-one.

Here is an example: prove that $f(x)={\frac {1-2x}{1+x}}$ is injective.

Since the notation is the notation for a function, the equation is a function. So we only need to prove that it is injective. Let $a$ and $b$ be the inputs of the function and that $f(a)=f(b)$. Thus,

${\frac {1-2a}{1+a}}={\frac {1-2b}{1+b}}$

$\Leftrightarrow (1+b)(1-2a)=(1+a)(1-2b)$

$\Leftrightarrow 1-2a+b-2ab=1-2b+a-2ab$
$\Leftrightarrow 1-2a+b=1-2b+a$

$\Leftrightarrow 1-2a+3b=1+a$

$\Leftrightarrow 1+3b=1+3a$

$\Leftrightarrow a=b$

So, the result is $a=b$, proving that the function is injective.

Another example is proving that $g(x)=x^{2}$ is not injective.

Using the same method, one can find that $a=\pm b$, which is not $a=b$. So, the function is not injective.

Resources

• One-to-one functions. Written notes created by Professor Esparza, UTSA.
• Functions, Wikibooks: Calculus
• One-to-one Functions and Inverses, University of Houston