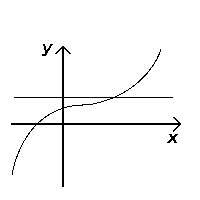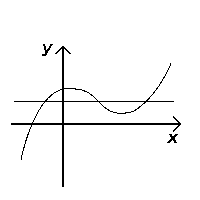One-to-one functions
To make it simple, for the function , all of the possible values constitute the domain, and all of the values ( on the x-y plane) constitute the range. To put it in more formal terms, a function is a mapping of some element , called the domain, to exactly one element , called the range, such that . The image below should help explain the modern definition of a function:
- A function is considered one-to-one if an element from domain of function , leads to exactly one element from range of the function. By definition, since only one element is mapped by function from some element , implies that there exists only one element from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to Figure 1.
The horizontal line and the algebraic 1-1 test
Similarly, the horizontal line test, though does not test if an equation is a function, tests if a function is injective (one-to-one). If any horizontal line ever touches the graph at more than one point, then the function is not one-to-one; if the line always touches at most one point on the graph, then the function is one-to-one.
The algebraic 1-1 test is the non-geometric way to see if a function is one-to-one. The basic concept is that:
Assume there is a function . If:
, and , then
function is one-to-one.
Here is an example: prove that is injective.
Since the notation is the notation for a function, the equation is a function. So we only need to prove that it is injective. Let and be the inputs of the function and that . Thus,
So, the result is , proving that the function is injective.
Another example is proving that is not injective.
Using the same method, one can find that , which is not . So, the function is not injective.
Resources
- One-to-one functions. Written notes created by Professor Esparza, UTSA.
- Functions, Wikibooks: Calculus
- One-to-one Functions and Inverses, University of Houston
Licensing
Content obtained and/or adapted from:
- Functions, Wikibooks: Calculus under a CC BY-SA license