Difference between revisions of "Bounded sets in Higher Dimensions"
| (One intermediate revision by the same user not shown) | |||
| Line 32: | Line 32: | ||
<p><em>In other words, a subset <span class="math-inline"><math>S</math></span> of <span class="math-inline"><math>\mathbb{R}^n</math></span> is bounded if <span class="math-inline"><math>S</math></span> is the subset of some ball in <span class="math-inline"><math>\mathbb{R}^n</math></span>.</em></p> | <p><em>In other words, a subset <span class="math-inline"><math>S</math></span> of <span class="math-inline"><math>\mathbb{R}^n</math></span> is bounded if <span class="math-inline"><math>S</math></span> is the subset of some ball in <span class="math-inline"><math>\mathbb{R}^n</math></span>.</em></p> | ||
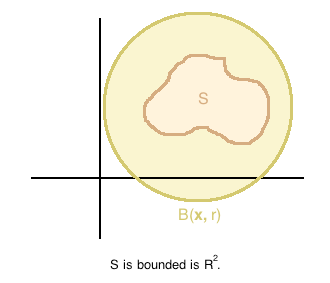
<p>In <span class="math-inline"><math>\mathbb{R}^2</math></span>, a set <span class="math-inline"><math>S \subseteq \mathbb{R}^2</math></span> that is bounded might look something like:</p> | <p>In <span class="math-inline"><math>\mathbb{R}^2</math></span>, a set <span class="math-inline"><math>S \subseteq \mathbb{R}^2</math></span> that is bounded might look something like:</p> | ||
| − | [[File:Bounded set in R2.png|Bounded set in <math>\R^2</math>]] | + | [[File:Bounded set in R2.png|center|Bounded set in <math>\R^2</math>]] |
<p>Meanwhile, a set <span class="math-inline"><math>S</math></span> that is unbounded might look something like:</p> | <p>Meanwhile, a set <span class="math-inline"><math>S</math></span> that is unbounded might look something like:</p> | ||
| − | [[File:Unbounded set in R2.png|Unbounded set in <math>\R^2</math>]] | + | [[File:Unbounded set in R2.png|center|Unbounded set in <math>\R^2</math>]] |
<p>For a more concrete example, consider the subset <span class="math-inline"><math>S = [0, 1) \times [0, 1) \subseteq \mathbb{R}^2</math></span>. Then the ball <span class="math-inline"><math>B(\mathbf{0}, 2)</math></span> is such that <span class="math-inline"><math>S \subseteq B(\mathbf{0}, 2)</math></span>, so <span class="math-inline"><math>S</math></span> is bounded. However, the subset <span class="math-inline"><math>S = \{ (x, y) \in \mathbb{R}^2 : x \geq 0, y \geq 0 \} \subseteq \mathbb{R}^2</math></span> is unbounded. To prove this, set <span class="math-inline"><math>\mathbf{x} = \mathbf{0}</math></span>. Suppose that there exists an <span class="math-inline"><math>r > 0</math></span> such that <span class="math-inline"><math>S \subseteq B(\mathbf{0}, r)</math></span>. now consider the point <span class="math-inline"><math>\mathbf{y} = (r+1, r+1) \in S</math></span>. Then:</p> | <p>For a more concrete example, consider the subset <span class="math-inline"><math>S = [0, 1) \times [0, 1) \subseteq \mathbb{R}^2</math></span>. Then the ball <span class="math-inline"><math>B(\mathbf{0}, 2)</math></span> is such that <span class="math-inline"><math>S \subseteq B(\mathbf{0}, 2)</math></span>, so <span class="math-inline"><math>S</math></span> is bounded. However, the subset <span class="math-inline"><math>S = \{ (x, y) \in \mathbb{R}^2 : x \geq 0, y \geq 0 \} \subseteq \mathbb{R}^2</math></span> is unbounded. To prove this, set <span class="math-inline"><math>\mathbf{x} = \mathbf{0}</math></span>. Suppose that there exists an <span class="math-inline"><math>r > 0</math></span> such that <span class="math-inline"><math>S \subseteq B(\mathbf{0}, r)</math></span>. now consider the point <span class="math-inline"><math>\mathbf{y} = (r+1, r+1) \in S</math></span>. Then:</p> | ||
| Line 40: | Line 40: | ||
<p>Therefore <span class="math-inline"><math>(r + 1, r + 1) \not \in B(\mathbf{0}, r)</math></span> for all <span class="math-inline"><math>r > 0</math></span>, but <span class="math-inline"><math>(r+1, r+1) \in S</math></span> for all <span class="math-inline"><math>r > 0</math></span>, so <span class="math-inline"><math>S \not \subseteq B(\mathbf{0}, r)</math></span> for all <span class="math-inline"><math>r > 0</math></span>, so <span class="math-inline"><math>S</math></span> is unbounded.</p> | <p>Therefore <span class="math-inline"><math>(r + 1, r + 1) \not \in B(\mathbf{0}, r)</math></span> for all <span class="math-inline"><math>r > 0</math></span>, but <span class="math-inline"><math>(r+1, r+1) \in S</math></span> for all <span class="math-inline"><math>r > 0</math></span>, so <span class="math-inline"><math>S \not \subseteq B(\mathbf{0}, r)</math></span> for all <span class="math-inline"><math>r > 0</math></span>, so <span class="math-inline"><math>S</math></span> is unbounded.</p> | ||
| + | |||
| + | == Licensing == | ||
| + | Content obtained and/or adapted from: | ||
| + | * [http://mathonline.wikidot.com/bounded-sets Bounded Sets, mathonline.wikidot.com] under a CC BY-SA license | ||
| + | * [http://mathonline.wikidot.com/bounded-subsets-in-euclidean-space Bounded Subsets in Euclidean Space, mathonline.wikidot.com] under a CC BY-SA license | ||
Latest revision as of 09:12, 8 November 2021
Bounded Sets
Consider the set . As you might imagine, there is no "largest" element in this set. If we were to claim that some element was the largest element in , then we note that and . There is a least element in this set though, namely . We can say that every element is such that . We could alternatively say that every element is such that or . We will now formally define this sort of idea.
Definition: Let where . We say that is bounded above by if for all , . We say that is bounded below by if for all , . We say that is bounded if it is both bounded above and bounded below, and we say that is unbounded if it is not both bounded above and below.
From this definition, we can intuitively say that the set of natural numbers is bounded below by any number . However, we note that is not bounded above since such as does not exist. Therefore in general we say that the set of natural numbers is not bounded.
Another example is the set . As we can guess, this set is bounded below by and bounded above by . Therefore we say that is bounded.
Sometimes a set might not be bounded above and might also not be bounded below. For example consider the set of integers which is clearly a subset of . This set is not bounded below and not bounded above.
We will now look at some theorems regarding bounded sets.
| Theorem 1: If and is a bounded set then is a bounded set. Further, if and is an unbounded set then is an unbounded set. |
- Proof: Let .
- For the first part of the proof, let be a bounded set and let be any lower bound to and let be any upper bound to . Then if , then , but we have that , and so , so is a bounded set.
- For the second part of the proof, let be an unbounded set and suppose instead that is a bounded set. Let be any lower bound to and let be any upper bound to . Then if , then , but we have that , and so , , so is bounded, but that contradicts the fact that is an unbounded set, so our assumption that was bounded is false. Therefore is an unbounded set.
Note that in the proof of Theorem 1, we could have omitted the second part of the proof since it is the contrapositive of the first part.
Bounded Subsets in Euclidean Space
Definition: Let . The set is said to be Bounded if there exists a and a positive real number such that and is said to be Unbounded otherwise.
In other words, a subset of is bounded if is the subset of some ball in .
In , a set that is bounded might look something like:
Meanwhile, a set that is unbounded might look something like:
For a more concrete example, consider the subset . Then the ball is such that , so is bounded. However, the subset is unbounded. To prove this, set . Suppose that there exists an such that . now consider the point . Then:
Therefore for all , but for all , so for all , so is unbounded.
Licensing
Content obtained and/or adapted from:
- Bounded Sets, mathonline.wikidot.com under a CC BY-SA license
- Bounded Subsets in Euclidean Space, mathonline.wikidot.com under a CC BY-SA license