Bounded sets in Higher Dimensions

Bounded Sets

Consider the set $\mathbb {N} =\{1,2,3,...\}$ . As you might imagine, there is no "largest" element in this set. If we were to claim that some element $u\in \mathbb {N}$ was the largest element in $\mathbb {N}$ , then we note that $u+1\in \mathbb {N}$ and $u<u+1$ . There is a least element in this set though, namely $1$ . We can say that every element $n\in \mathbb {N}$ is such that $1\leq n$ . We could alternatively say that every element $n\in \mathbb {N}$ is such that $0\leq n$ or $-3234\leq n$ . We will now formally define this sort of idea.

Definition: Let $S\subseteq \mathbb {R}$ where $S\neq \emptyset$ . We say that $S$ is bounded above by $M$ if for all $x\in \mathbb {S}$ , $x\leq M$ . We say that $S$ is bounded below by $m$ if for all $x\in \mathbb {S}$ , $m\leq x$ . We say that $S$ is bounded if it is both bounded above and bounded below, and we say that $S$ is unbounded if it is not both bounded above and below.

From this definition, we can intuitively say that the set of natural numbers $\mathbb {N}$ is bounded below by any number $m\leq 1$ . However, we note that $\mathbb {N}$ is not bounded above since such as $M$ does not exist. Therefore in general we say that the set of natural numbers is not bounded.

Another example is the set $S:=\{x\in \mathbb {R} :-2\leq x\leq 2\}$ . As we can guess, this set $S$ is bounded below by $m=-2$ and bounded above by $M=2$ . Therefore we say that $S$ is bounded.

Sometimes a set might not be bounded above and might also not be bounded below. For example consider the set of integers $\mathbb {Z}$ which is clearly a subset of $\mathbb {R}$ . This set is not bounded below and not bounded above.

We will now look at some theorems regarding bounded sets.

Theorem 1: If

A\subseteq B

and

B

is a bounded set then

A

is a bounded set. Further, if

A\subseteq B

and

A

is an unbounded set then

B

is an unbounded set.

Proof: Let $A\subseteq B$ .

For the first part of the proof, let $B$ be a bounded set and let $m$ be any lower bound to $B$ and let $M$ be any upper bound to $B$ . Then if $x\in A$ , then $x\in B$ , but $\forall x\in B$ we have that $m\leq x\leq M$ , and so $\forall x\in A$ , $m\leq x\leq M$ so $A$ is a bounded set.

For the second part of the proof, let $A$ be an unbounded set and suppose instead that $B$ is a bounded set. Let $m$ be any lower bound to $B$ and let $M$ be any upper bound to $B$ . Then if $x\in A$ , then $x\in B$ , but $\forall x\in B$ we have that $m\leq x\leq M$ , and so $\forall x\in A$ , $m\leq x\leq M$ , so $A$ is bounded, but that contradicts the fact that $A$ is an unbounded set, so our assumption that $B$ was bounded is false. Therefore $B$ is an unbounded set. $\blacksquare$

Note that in the proof of Theorem 1, we could have omitted the second part of the proof since it is the contrapositive of the first part.

Bounded Subsets in Euclidean Space

Definition: Let $S\subseteq \mathbb {R} ^{n}$ . The set $S$ is said to be Bounded if there exists a $\mathbf {x} \in \mathbb {R} ^{n}$ and a positive real number $r>0$ such that $S\subseteq B(\mathbf {x} ,r)$ and $S$ is said to be Unbounded otherwise.

In other words, a subset $S$ of $\mathbb {R} ^{n}$ is bounded if $S$ is the subset of some ball in $\mathbb {R} ^{n}$ .

In $\mathbb {R} ^{2}$ , a set $S\subseteq \mathbb {R} ^{2}$ that is bounded might look something like:

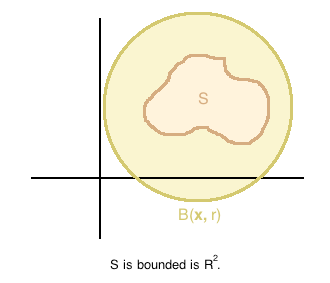
Bounded set in '"`UNIQ--postMath-00000053-QINU`"'

Meanwhile, a set $S$ that is unbounded might look something like:

Unbounded set in '"`UNIQ--postMath-00000055-QINU`"'

For a more concrete example, consider the subset $S=[0,1)\times [0,1)\subseteq \mathbb {R} ^{2}$ . Then the ball $B(\mathbf {0} ,2)$ is such that $S\subseteq B(\mathbf {0} ,2)$ , so $S$ is bounded. However, the subset $S=\{(x,y)\in \mathbb {R} ^{2}:x\geq 0,y\geq 0\}\subseteq \mathbb {R} ^{2}$ is unbounded. To prove this, set $\mathbf {x} =\mathbf {0}$ . Suppose that there exists an $r>0$ such that $S\subseteq B(\mathbf {0} ,r)$ . now consider the point $\mathbf {y} =(r+1,r+1)\in S$ . Then:

{\begin{aligned}\quad \|\mathbf {r} -\mathbf {0} \|={\sqrt {(r+1)^{2}+(r+1)^{2}}}={\sqrt {2}}\mid r+1\mid >r\end{aligned}}

Therefore $(r+1,r+1)\not \in B(\mathbf {0} ,r)$ for all $r>0$ , but $(r+1,r+1)\in S$ for all $r>0$ , so $S\not \subseteq B(\mathbf {0} ,r)$ for all $r>0$ , so $S$ is unbounded.