Difference between revisions of "Angles and their measure"
Rylee.taylor (talk | contribs) (fixing link to go straight to pdf) |
|||
| Line 1: | Line 1: | ||
| + | ==Angular Measurement and Circular Sectors== | ||
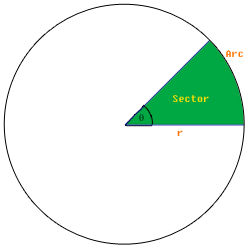
| + | A section of a circle is known as a sector. One side of the sector is the radius. The portion of the cirumference that is included in the sector is known as an arc. | ||
| + | |||
| + | [[Image:SectorArc.png]] | ||
| + | |||
| + | ===Angular Degree=== | ||
| + | A circle has 360 degrees. Each degree can have 60 minutes (designated as ' ) and each minute can have 60 seconds (designated as " ). Since we can not convert minutes or seconds into radians directly we need to convert the minutes and seconds into a decimal number. Here is the formula:<p> | ||
| + | Convert <math>X^\circ</math> Y' Z" into degrees. | ||
| + | |||
| + | <math>X + \left (Y \times \frac{1}{60} \right ) + \left (Z \times \frac{1}{3600} \right ) = X + \frac{Y}{60}+ \frac{Z}{3600}</math> | ||
| + | |||
| + | For a practical example, convert <math>23^\circ</math> 18' 38" into degrees. | ||
| + | |||
| + | <math>23 + \frac{18}{60}+ \frac{38}{3600} = 23.3106</math> | ||
| + | |||
| + | == Classification of Angles by Degree Measure == | ||
| + | '''Acute Angle''' | ||
| + | *an angle is said to be acute if it measures between 0 and 90 degrees, exclusive. | ||
| + | [[File:Ángulo agudo.svg|150px|Acute Angle]] | ||
| + | |||
| + | '''Right Angle''' | ||
| + | *an angle is said to be right if it measures 90 degrees. | ||
| + | *notice the small box placed in the corner of a right angle, unless the box is present it is not assumed the angle is 90 degrees. | ||
| + | *all right angles are congruent | ||
| + | [[File:Right angle.svg|100px]] | ||
| + | |||
| + | '''Obtuse Angle''' | ||
| + | *an angle is said to be obtuse if it measures between 90 and 180 degrees, exclusive. | ||
| + | [[File:Ángulo obtuso.svg|150px|Obtuse Angle]] | ||
| + | |||
| + | ===Angular Radian=== | ||
| + | A radian is the angle subtended at the centre of a circle by an arc of its circumference equal in length to the radius of the circle. Since we know that that the formula for the circumference of a circle is <math>C = 2 \pi r</math> we can determine that there are <math>2 \pi</math> radians in a circle. We abbreviate radians as rad. | ||
| + | |||
| + | ===Conversion Between Degrees and Radians=== | ||
| + | Mathematics requires us to use radians for most angular measurements. Therefore we need to know how to convert from degrees to radians Since we know that there are <math>360^\circ</math> degrees or <math>2 \pi</math> radians in a circle. We can determine these equations: | ||
| + | <math>1^\circ = \frac {\pi }{180}</math> | ||
| + | |||
| + | <math>1\ radian = \frac {180}{\pi }</math> | ||
| + | |||
| + | So we can write these general formulae. | ||
| + | |||
| + | <math>X^\circ = \frac {X \times \pi }{180}</math> | ||
| + | |||
| + | <math>X\ radian \left(s \right ) = \frac {X \times 180}{\pi }</math> | ||
| + | |||
| + | Here is an example convert <math>20^\circ</math> into radians | ||
| + | |||
| + | <math>20^\circ = \frac {20 \times \pi }{180} = \frac{1}{9} \pi\ rad</math> | ||
| + | |||
| + | Convert <math>\frac{1}{9} \pi</math> into degrees. | ||
| + | |||
| + | <math>\frac{1}{9} \pi\ radian \left(s \right ) = \frac {\frac{1}{9} \pi \times 180}{\pi } = 20^\circ </math> | ||
| + | |||
| + | ==The unit circle== | ||
| + | [[File:Unit Circle Definitions of Six Trigonometric Functions.png|thumb|264x264px|The center of the unit circle is the origin <math>O</math>, point <math>A=(x_A,y_A)</math>. Creating line segments starting from point <math>A</math> to <math>x</math> on the <math>x</math>-axis will create two line segments. From this, we learn that, in terms of <math>\theta</math>, point <math>A=(\cos\theta,\sin\theta)</math>and other properties.]] | ||
| + | A circle with the equation <math>x^2+y^2=1</math> is called a ''unit circle''. Imagine a circle with center at the origin of a [[wikipedia:Cartesian_coordinate_system|Cartesian coordinate system]]. | ||
| + | |||
| + | Rotating a ray from the direction of the positive half of the ''x''-axis by an angle <math>\theta</math> (counterclockwise for <math>\theta > 0,</math> and clockwise for <math>\theta < 0</math>) yields intersection points of this ray with the unit {{nowrap|circle: <math>\mathrm{A} = (x_\mathrm{A},y_\mathrm{A})</math>,}} and, by extending the ray to a line if necessary, with the {{nowrap|line <math> \text{“}x=1\text{”}:\;\mathrm{B} = (x_\mathrm{B},y_\mathrm{B}),</math>}} and with the {{nowrap|line <math> \text{“}y=1\text{”}:\;\mathrm{C} = (x_\mathrm{C},y_\mathrm{C}).</math>}} The tangent line to the unit circle in point {{math|A}}, which is orthogonal to this ray, intersects the ''y''- and ''x''-axis at points <math>\mathrm{D} = (0,y_\mathrm{D})</math> and <math>\mathrm{E} = (x_\mathrm{E},0)</math>. The coordinate values of these points give all the existing values of the trigonometric functions for arbitrary real values of <math>\theta</math> in the following manner: | ||
| + | <center> | ||
| + | {| class="wikitable" | ||
| + | |+Trigonometric functions and the unit circle | ||
| + | !Function | ||
| + | !Right-triangle definition | ||
| + | !Unit circle definition | ||
| + | |- | ||
| + | !<math>\sin\theta</math> | ||
| + | |align=center|{{sfrac|opposite|hypotenuse}} | ||
| + | |<math>y_A</math> | ||
| + | |- | ||
| + | !<math>\cos\theta</math> | ||
| + | |align=center|{{sfrac|adjacent|hypotenuse}} | ||
| + | |<math>x_A</math> | ||
| + | |- | ||
| + | !<math>\tan\theta</math> | ||
| + | |align=center|{{Sfrac|opposite|adjacent}} | ||
| + | |<math>y_B=\frac{y_A}{x_A}</math> | ||
| + | |- | ||
| + | !<math>\csc\theta</math> | ||
| + | |align=center|{{Sfrac|hypotenuse|opposite}} | ||
| + | |<math>y_D=\frac{1}{y_A}</math> | ||
| + | |- | ||
| + | !<math>\sec\theta</math> | ||
| + | |align=center|{{Sfrac|hypotenuse|adjacent}} | ||
| + | |<math>x_E=\frac{1}{x_A}</math> | ||
| + | |- | ||
| + | !<math>\cot\theta</math> | ||
| + | |align=center|{{Sfrac|adjacent|opposite}} | ||
| + | |<math>x_C=\frac{x_A}{y_A}</math> | ||
| + | |} | ||
| + | </center> | ||
| + | The importance of the unit circle is that it expands the definitions of trigonometric functions. Before, those values are constrained within a right triangle. Now, the functions can be used on any radian as their input. | ||
| + | |||
| + | ==Resources== | ||
* [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Angles%20and%20their%20measure/Esparza%201093%20Notes%202.1.pdf Angles and their measure]. Written notes created by Professor Esparza, UTSA. | * [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Angles%20and%20their%20measure/Esparza%201093%20Notes%202.1.pdf Angles and their measure]. Written notes created by Professor Esparza, UTSA. | ||
Revision as of 14:12, 5 October 2021
Contents
Angular Measurement and Circular Sectors
A section of a circle is known as a sector. One side of the sector is the radius. The portion of the cirumference that is included in the sector is known as an arc.
Angular Degree
A circle has 360 degrees. Each degree can have 60 minutes (designated as ' ) and each minute can have 60 seconds (designated as " ). Since we can not convert minutes or seconds into radians directly we need to convert the minutes and seconds into a decimal number. Here is the formula:
Convert Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^\circ} Y' Z" into degrees. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X + \left (Y \times \frac{1}{60} \right ) + \left (Z \times \frac{1}{3600} \right ) = X + \frac{Y}{60}+ \frac{Z}{3600}} For a practical example, convert 18' 38" into degrees.
Classification of Angles by Degree Measure
Acute Angle
- an angle is said to be acute if it measures between 0 and 90 degrees, exclusive.
Right Angle
- an angle is said to be right if it measures 90 degrees.
- notice the small box placed in the corner of a right angle, unless the box is present it is not assumed the angle is 90 degrees.
- all right angles are congruent
Obtuse Angle
- an angle is said to be obtuse if it measures between 90 and 180 degrees, exclusive.
Angular Radian
A radian is the angle subtended at the centre of a circle by an arc of its circumference equal in length to the radius of the circle. Since we know that that the formula for the circumference of a circle is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = 2 \pi r} we can determine that there are radians in a circle. We abbreviate radians as rad.
Conversion Between Degrees and Radians
Mathematics requires us to use radians for most angular measurements. Therefore we need to know how to convert from degrees to radians Since we know that there are degrees or radians in a circle. We can determine these equations: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1^\circ = \frac {\pi }{180}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1\ radian = \frac {180}{\pi }}
So we can write these general formulae.
Here is an example convert into radians
Convert into degrees.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{9} \pi\ radian \left(s \right ) = \frac {\frac{1}{9} \pi \times 180}{\pi } = 20^\circ }
The unit circle

A circle with the equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+y^2=1} is called a unit circle. Imagine a circle with center at the origin of a Cartesian coordinate system.
Rotating a ray from the direction of the positive half of the x-axis by an angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} (counterclockwise for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta > 0,} and clockwise for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta < 0} ) yields intersection points of this ray with the unit Template:Nowrap and, by extending the ray to a line if necessary, with the Template:Nowrap and with the Template:Nowrap The tangent line to the unit circle in point A, which is orthogonal to this ray, intersects the y- and x-axis at points Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{D} = (0,y_\mathrm{D})} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{E} = (x_\mathrm{E},0)} . The coordinate values of these points give all the existing values of the trigonometric functions for arbitrary real values of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} in the following manner:
| Function | Right-triangle definition | Unit circle definition |
|---|---|---|
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin\theta} | Template:Sfrac | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_A} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\theta} | Template:Sfrac | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_A} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan\theta} | Template:Sfrac | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_B=\frac{y_A}{x_A}} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \csc\theta} | Template:Sfrac | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_D=\frac{1}{y_A}} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sec\theta} | Template:Sfrac | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_E=\frac{1}{x_A}} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cot\theta} | Template:Sfrac | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_C=\frac{x_A}{y_A}} |
The importance of the unit circle is that it expands the definitions of trigonometric functions. Before, those values are constrained within a right triangle. Now, the functions can be used on any radian as their input.
Resources
- Angles and their measure. Written notes created by Professor Esparza, UTSA.