Polar Coordinates

A polar grid with several angles labeled in degrees

The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by an angle and a distance. The polar coordinate system is especially useful in situations where the relationship between two points is most easily expressed in terms of angles and distance; in the more familiar Cartesian coordinate system or rectangular coordinate system, such a relationship can only be found through trigonometric formulae.

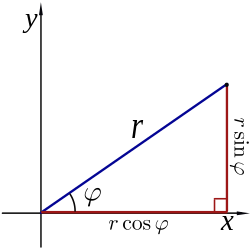
As the coordinate system is two-dimensional, each point is determined by two polar coordinates: the radial coordinate and the angular coordinate. The radial coordinate (usually denoted as $r$) denotes the point's distance from a central point known as the pole (equivalent to the origin in the Cartesian system). The angular coordinate (also known as the polar angle or the azimuth angle, and usually denoted by $\theta$ or $t$) denotes the positive or anticlockwise (counterclockwise) angle required to reach the point from the 0° ray or polar axis (which is equivalent to the positive $x$-axis in the Cartesian coordinate plane).

Plotting points with polar coordinates

The points (3,60°) and (4,210°) on a polar coordinate system

Each point in the polar coordinate system can be described with the two polar coordinates, which are usually called $r$ (the radial coordinate) and θ (the angular coordinate, polar angle, or azimuth angle, sometimes represented as $\phi$ or $t$). The $r$ coordinate represents the radial distance from the pole, and the θ coordinate represents the anticlockwise (counterclockwise) angle from the $0^{\circ }$ ray (sometimes called the polar axis), known as the positive $x$-axis on the Cartesian coordinate plane.

For example, the polar coordinates $(3,60^{\circ })$ would be plotted as a point 3 units from the pole on the $60^{\circ }$ ray. The coordinates $(-3,240^{\circ })$ would also be plotted at this point because a negative radial distance is measured as a positive distance on the opposite ray (the ray reflected about the origin, which differs from the original ray by $180^{\circ }$).

One important aspect of the polar coordinate system, not present in the Cartesian coordinate system, is that a single point can be expressed with an infinite number of different coordinates. This is because any number of multiple revolutions can be made around the central pole without affecting the actual location of the point plotted. In general, the point $(r,\theta )$ can be represented as $(r,\theta \pm 360^{\circ }k)$ or $(-r,\theta \pm (2k+1)180^{\circ })$ , where $k$ is any integer.

The arbitrary coordinates $(0,\theta )$ are conventionally used to represent the pole, as regardless of the θ coordinate, a point with radius 0 will always be on the pole. To get a unique representation of a point, it is usual to limit $r$ to negative and non-negative numbers $r\geq 0$ and $\theta$ to the interval $[0,360^{\circ })$ or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-180^\circ,180^\circ]} (or, in radian measure, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,2\pi)} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-\pi,\pi]} ).

Angles in polar notation are generally expressed in either degrees or radians, using the conversion Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi\ \text{rad}=360^\circ} . The choice depends largely on the context. Navigation applications use degree measure, while some physics applications (specifically rotational mechanics) and almost all mathematical literature on calculus use radian measure.

Converting between polar and Cartesian coordinates

A diagram illustrating the conversion formulae

The two polar coordinates Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r,\theta} can be converted to the Cartesian coordinates Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,y} by using the trigonometric functions sine and cosine:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=r\cos(\theta)}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=r\sin(\theta)}

while the two Cartesian coordinates Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,y} can be converted to polar coordinate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} by

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\sqrt{x^2+y^2}} (by a simple application of the Pythagorean theorem).

To determine the angular coordinate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} , the following two ideas must be considered:

• For Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=0} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} can be set to any real value.
• For Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\ne0} , to get a unique representation for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} , it must be limited to an interval of size Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi} . Conventional choices for such an interval are Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,2\pi)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-\pi,\pi]} .

To obtain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} in the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,2\pi)} , the following may be used (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \arctan} denotes the inverse of the tangent function):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta= \begin{cases} \arctan\left(\frac{y}{x}\right)&\text{if }x>0\text{ and }y\ge0\\ \arctan\left(\frac{y}{x}\right)+2\pi&\text{if }x>0\text{ and }y<0\\ \arctan\left(\frac{y}{x}\right)+\pi&\text{if }x<0\\ \frac{\pi}{2}&\text{if }x=0\text{ and }y>0\\ \frac{3\pi}{2}&\text{if }x=0\text{ and }y<0 \end{cases}}

To obtain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} in the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-\pi,\pi]} , the following may be used:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta= \begin{cases} \arctan\left(\frac{y}{x}\right)&\text{if }x>0\\ \arctan\left(\frac{y}{x}\right)+\pi&\text{if }x<0\text{ and }y\ge0\\ \arctan\left(\frac{y}{x}\right)-\pi&\text{if }x<0\text{ and }y<0\\ \frac{\pi}{2}&\text{if }x=0\text{ and }y>0\\ -\frac{\pi}{2}&\text{if }x=0\text{ and }y<0 \end{cases}}

One may avoid having to keep track of the numerator and denominator signs by use of the atan2 function, which has separate arguments for the numerator and the denominator.

Polar equations

The equation defining an algebraic curve expressed in polar coordinates is known as a polar equation. In many cases, such an equation can simply be specified by defining Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} as a function of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} . The resulting curve then consists of points of the form ${\big (}r(\theta ),\theta {\big )}$ and can be regarded as the graph of the polar function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} .

Different forms of symmetry can be deduced from the equation of a polar function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} . If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(-\theta)=r(\theta)} the curve will be symmetrical about the horizontal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0^\circ/180^\circ)} ray, if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\pi-\theta)=r(\theta)} it will be symmetric about the vertical Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (90^\circ/270^\circ)} ray, and if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta-\alpha^\circ)=r(\theta)} it will be rotationally symmetric Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha^\circ} counterclockwise about the pole.

Because of the circular nature of the polar coordinate system, many curves can be described by a rather simple polar equation, whereas their Cartesian form is much more intricate. Among the best known of these curves are the polar rose, Archimedean spiral, lemniscate, limaçon, and cardioid.

For the circle, line, and polar rose below, it is understood that there are no restrictions on the domain and range of the curve.

Circle

A circle with equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta)=1}

The general equation for a circle with a center at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (r_0,\phi)} and radius Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r^2-2rr_0\cos(\theta-\phi)+r_0^2=a^2}

This can be simplified in various ways, to conform to more specific cases, such as the equation

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta)=a}

for a circle with a center at the pole and radius Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} .

Line

Radial lines (those running through the pole) are represented by the equation

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\phi}

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} is the angle of elevation of the line; that is, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=\arctan(m)} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the slope of the line in the Cartesian coordinate system. The non-radial line that crosses the radial line Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\phi} perpendicularly at the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (r_0,\phi)} has the equation

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta)=r_0\sec(\theta-\phi)}

Polar rose

A polar rose with equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta)=2\sin(4\theta)}

A polar rose is a famous mathematical curve that looks like a petaled flower, and that can be expressed as a simple polar equation,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta)=a\cos(k\theta+\phi_0)}

for any constant Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_0} (including 0). If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is an integer, these equations will produce a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -petaled rose if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is odd, or a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2k} -petaled rose if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is even. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is rational but not an integer, a rose-like shape may form but with overlapping petals. Note that these equations never define a rose with 2, 6, 10, 14, etc. petals. The variable Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} represents the length of the petals of the rose.

Archimedean spiral

One arm of an Archimedean spiral with equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta)=\theta} for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\in(0,6\pi)}

The Archimedean spiral is a famous spiral that was discovered by Archimedes, which also can be expressed as a simple polar equation. It is represented by the equation

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(\theta)=a+b\theta}

Changing the parameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} will turn the spiral, while Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} controls the distance between the arms, which for a given spiral is always constant. The Archimedean spiral has two arms, one for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta>0} and one for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta<0} . The two arms are smoothly connected at the pole. Taking the mirror image of one arm across the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 90^\circ/270^\circ} line will yield the other arm. This curve is notable as one of the first curves, after the conic sections, to be described in a mathematical treatise, and as being a prime example of a curve that is best defined by a polar equation.

Conic sections

Ellipse, showing semi-latus rectum

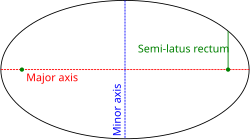
A conic section with one focus on the pole and the other somewhere on the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0^\circ} ray (so that the conic's semi-major axis lies along the polar axis) is given by:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\frac{\ell}{1+\epsilon\cos(\theta)}}

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} is the eccentricity and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell} is the semi-latus rectum (the perpendicular distance at a focus from the major axis to the curve).

1. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon>1} , this equation defines a hyperbola.
2. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=1} , it defines a parabola.
3. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<\epsilon<1} , it defines an ellipse. The special case Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=0} of the latter results in a circle of radius Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell} .

Resources

• Polar Coordinates. Written notes created by Professor Esparza, UTSA.
• Polar Coordinates Basic Introduction, Conversion to Rectangular, How to Plot Points, Negative R Value Video by The Organic Chemistry Tutor 2017
• Polar Coordinates - The Basics Video by patrickJMT 2018

Licensing

Content obtained and/or adapted from:

• Polar Introduction, Wikibooks under a CC BY-SA license