Abstract Algebra: Preliminaries
Contents
Natural numbers
The natural numbers are those numbers used for counting (as in "there are six coins on the table") and ordering (as in "this is the third largest city in the country"). In common mathematical terminology, words colloquially used for counting are "cardinal numbers", and words used for ordering are "ordinal numbers". The natural numbers can, at times, appear as a convenient set of codes (labels or "names"), that is, as what linguists call nominal numbers, forgoing many or all of the properties of being a number in a mathematical sense.
Some definitions begin the natural numbers with 0, corresponding to the non-negative integers {0, 1, 2, 3, ...}, whereas others start with 1, corresponding to the positive integers {1, 2, 3, ...}. Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers).
The natural numbers are a basis from which many other number sets may be built by extension: the integers, by including (if not yet in) the neutral element 0 and an additive inverse (−n) for each nonzero natural number n; the rational numbers, by including a multiplicative inverse () for each nonzero integer n (and also the product of these inverses by integers); the real numbers by including with the rationals the limits of (converging) Cauchy sequences of rationals; the complex numbers, by including with the real numbers the unresolved square root of minus one (and also the sums and products thereof); and so on. This chain of extensions make the natural numbers canonically embedded (identified) in the other number systems.
In common language, particularly in primary school education, natural numbers may be called counting numbers to intuitively exclude the negative integers and zero, and also to contrast the discreteness of counting to the continuity of measurement — a hallmark characteristic of real numbers.
Well-ordering principle
Consider the following set which we define to be the set of natural numbers:
Now consider any subset of . For example, let us consider the subsets , , and . The subset describes a finite set containing two integers. The subset describes the infinite set of all odd natural numbers, and the subset describes the infinite set of all even natural numbers. Notice that in each of these cases we can identify a least element of the subset. For example, the least element in is , the least element in is , and the least element in is .
In fact, it is impossible to construct a nonempty subset of that does not contain a least element. We describe this very important result below in the following theorem.
Theorem 1 (The Well-Ordering Principle of the Natural Numbers): Let be a nonempty subset of the natural numbers . Then there exists a least element , that is, for all .
We do not have the tools to prove Theorem 1 although it is a rather intuitively obvious result. Nevertheless, we should note that while Theorem 1 holds true for the set of natural numbers, it does not hold true for all sets of real numbers. For example, consider the set of rational numbers :
Any subset of the rational numbers need not have a least element. For example, consider the following subset of rational numbers between and noninclusive, that is, . We claim that has no least element. To prove this, assume that does have a least element, say is such that for all . Since we have that where Since we must have that too since and so:
Consider the number in the middle of and . This number is . Since and we have that and , so indeed, and which is a contradiction to our assumption that a least element exists in .
It's important to note that while not every subset of the rational numbers contains a least element, there are still subsets of that do contain a least element.
Induction
Mathematical induction is a mathematical proof technique. It is essentially used to prove that a statement P(n) holds for every natural number n = 0, 1, 2, 3, . . . ; that is, the overall statement is a sequence of infinitely many cases P(0), P(1), P(2), P(3), . . . . Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder:
"Mathematical induction proves that we can climb as high as we like on a ladder, by proving that we can climb onto the bottom rung (the basis) and that from each rung we can climb up to the next one (the step)."
- — Concrete Mathematics, page 3 margins.
A proof by induction consists of two cases. The first, the base case (or basis), proves the statement for n = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that if the statement holds for any given case n = k, then it must also hold for the next case n = k + 1. These two steps establish that the statement holds for every natural number n. The base case does not necessarily begin with n = 0, but often with n = 1, and possibly with any fixed natural number n = N, establishing the truth of the statement for all natural numbers n ≥ N.
Description
The simplest and most common form of mathematical induction infers that a statement involving a natural number n (that is, an integer n ≥ 0 or 1) holds for all values of n. The proof consists of two steps:
- The initial or base case: prove that the statement holds for 0, or 1.
- The induction step, inductive step, or step case: prove that for every n, if the statement holds for n, then it holds for n + 1. In other words, assume that the statement holds for some arbitrary natural number n, and prove that the statement holds for n + 1.
The hypothesis in the inductive step, that the statement holds for a particular n, is called the induction hypothesis or inductive hypothesis. To prove the inductive step, one assumes the induction hypothesis for n and then uses this assumption to prove that the statement holds for n + 1.
Authors who prefer to define natural numbers to begin at 0 use that value in the base case; those who define natural numbers to begin at 1 use that value.
Example
Mathematical induction can be used to prove the following statement P(n) for all natural numbers n.
This states a general formula for the sum of the natural numbers less than or equal to a given number; in fact an infinite sequence of statements: , , , etc.
Proposition. For any ,
Proof. Let P(n) be the statement We give a proof by induction on n.
Base case: Show that the statement holds for the smallest natural number n = 0.
P(0) is clearly true:
Inductive step: Show that for any k ≥ 0, if P(k) holds, then P(k+1) also holds.
Assume the induction hypothesis that for a particular k, the single case n = k holds, meaning P(k) is true:
It follows that:
Algebraically, the right hand side simplifies as:
Equating the extreme left hand and right hand sides, we deduce that:
That is, the statement P(k+1) also holds true, establishing the inductive step.
Conclusion: Since both the base case and the inductive step have been proved as true, by mathematical induction the statement P(n) holds for every natural number n. ∎
Integers
The set of integers consists of zero (0), the positive natural numbers (1, 2, 3, ...), also called whole numbers or counting numbers, and their additive inverses (the negative integers, i.e., −1, −2, −3, ...). The set of integers is often denoted by the boldface (Z) or blackboard bold letter "Z"—standing originally for the German word Zahlen ("numbers").
is a subset of the set of all rational numbers , which in turn is a subset of the real numbers . Like the natural numbers, is countably infinite.
Algebraic properties
Like the natural numbers, is closed under the operations of addition and multiplication, that is, the sum and product of any two integers is an integer. However, with the inclusion of the negative natural numbers (and importantly, 0), , unlike the natural numbers, is also closed under subtraction.
The integers form a unital ring which is the most basic one, in the following sense: for any unital ring, there is a unique ring homomorphism from the integers into this ring. This universal property, namely to be an initial object in the category of rings, characterizes the ring .
is not closed under division, since the quotient of two integers (e.g., 1 divided by 2) need not be an integer. Although the natural numbers are closed under exponentiation, the integers are not (since the result can be a fraction when the exponent is negative).
The following table lists some of the basic properties of addition and multiplication for any integers a, b and c:
| Addition | Multiplication | |
|---|---|---|
| Closure: | a + b is an integer | a × b is an integer |
| Associativity: | a + (b + c) (a + b) + c | a × (b × c) (a × b) × c |
| Commutativity: | a + b b + a | a × b b × a |
| Existence of an identity element: | a + 0 a | a × 1 a |
| Existence of inverse elements: | a + (−a) 0 | The only invertible integers (called units) are −1 and 1. |
| Distributivity: | a × (b + c) (a × b) + (a × c) and (a + b) × c (a × c) + (b × c) | |
| No zero divisors: | If a × b 0, then a 0 or b 0 (or both) | |
The first five properties listed above for addition say that , under addition, is an abelian group. It is also a cyclic group, since every non-zero integer can be written as a finite sum 1 + 1 + ... + 1 or (−1) + (−1) + ... + (−1). In fact, under addition is the only infinite cyclic group—in the sense that any infinite cyclic group is isomorphic to .
The first four properties listed above for multiplication say that under multiplication is a commutative monoid. However, not every integer has a multiplicative inverse (as is the case of the number 2), which means that under multiplication is not a group.
All the rules from the above property table (except for the last), when taken together, say that together with addition and multiplication is a commutative ring with unity. It is the prototype of all objects of such algebraic structure. Only those equalities of expressions are true in for all values of variables, which are true in any unital commutative ring. Certain non-zero integers map to zero in certain rings.
The lack of zero divisors in the integers (last property in the table) means that the commutative ring is an integral domain.
The lack of multiplicative inverses, which is equivalent to the fact that is not closed under division, means that is not a field. The smallest field containing the integers as a subring is the field of rational numbers. The process of constructing the rationals from the integers can be mimicked to form the field of fractions of any integral domain. And back, starting from an algebraic number field (an extension of rational numbers), its ring of integers can be extracted, which includes as its subring.
Although ordinary division is not defined on , the division "with remainder" is defined on them. It is called Euclidean division, and possesses the following important property: given two integers a and b with b ≠ 0, there exist unique integers q and r such that a q × b + r and 0 ≤ r < |b|, where |b| denotes the absolute value of b. The integer q is called the quotient and r is called the remainder of the division of a by b. The Euclidean algorithm for computing greatest common divisors works by a sequence of Euclidean divisions.
The above says that is a Euclidean domain. This implies that is a principal ideal domain, and any positive integer can be written as the products of primes in an essentially unique way. This is the fundamental theorem of arithmetic.
Construction
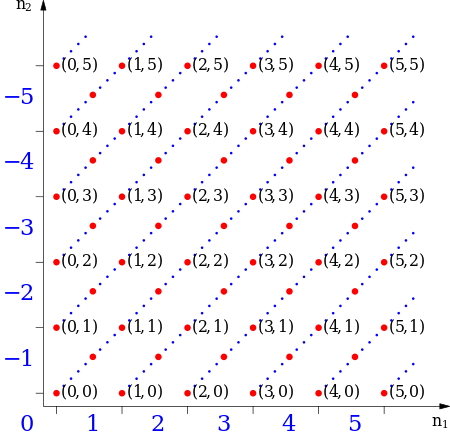
In elementary school teaching, integers are often intuitively defined as the (positive) natural numbers, zero, and the negations of the natural numbers. However, this style of definition leads to many different cases (each arithmetic operation needs to be defined on each combination of types of integer) and makes it tedious to prove that integers obey the various laws of arithmetic. Therefore, in modern set-theoretic mathematics, a more abstract construction allowing one to define arithmetical operations without any case distinction is often used instead. The integers can thus be formally constructed as the equivalence classes of ordered pairs of natural numbers (a,b).
The intuition is that (a,b) stands for the result of subtracting b from a. To confirm our expectation that 1 − 2 and 4 − 5 denote the same number, we define an equivalence relation ~ on these pairs with the following rule:
precisely when
Addition and multiplication of integers can be defined in terms of the equivalent operations on the natural numbers; by using [(a,b)] to denote the equivalence class having (a,b) as a member, one has:
The negation (or additive inverse) of an integer is obtained by reversing the order of the pair:
Hence subtraction can be defined as the addition of the additive inverse:
The standard ordering on the integers is given by:
- if and only if
It is easily verified that these definitions are independent of the choice of representatives of the equivalence classes.
Every equivalence class has a unique member that is of the form (n,0) or (0,n) (or both at once). The natural number n is identified with the class [(n,0)] (i.e., the natural numbers are embedded into the integers by map sending n to [(n,0)]), and the class [(0,n)] is denoted −n (this covers all remaining classes, and gives the class [(0,0)] a second time since −0 0.
Thus, [(a,b)] is denoted by
If the natural numbers are identified with the corresponding integers (using the embedding mentioned above), this convention creates no ambiguity.
This notation recovers the familiar representation of the integers as {..., −2, −1, 0, 1, 2, ...} .
Some examples are:
Division algorithm
One rather important aspect of the divisibility of integers is that if then can be written as the product of some quotient with plus a remainder . For example, if and , then where and .
The following theorem known as the Division Algorithm shows us that for any pair of integers where that the form exists and is unique.
Theorem 1 (The Division Algorithm): Let with . Then there exists unique where and such that .
The value of is often called the Remainder when is divided by . That is, is equal to some multiple , known as the Quotient of , plus a remainder for which .
- Proof: Let with and consider the following set :
- Consider of nonnegative elements in . If then and if then , so is a nonempty set. Moreover, is a nonempty subset of integers and so by the Well-Ordering principle there exists a least element of , say is this least element. Since we have that for some and so:
- So if of the form we desire. Now since and every element in is nonnegative then we have that . Suppose that . Then where and so:
- Therefore and so . Since and we have that . But this implies that is not the least element of which is a contradiction, so our assumption that is false, and so .
- We lastly show that and are unique for and . Suppose that and where . Then by subtracting these two equations we get:
- Therefore is a multiple of . Since and we must have that . The only multiple of such that is , so:
- Since , we have that . Since this implies that and so . Therefore can be uniquely expressed in the form where .
Congruence modulo m
Definition: If then we say that is Congruent to modulo denoted if .
The congruence of two integers is an equivalence relation which we can describe in other words. We say that and are said to be congruent modulo if divided by leaves the same remaining as divided by .
For example, since . Notice also that when and are divided by they both leave the same remainder, .
We can denote the remainder of an integer when divided by as simply . For example, since the remaining of when divided by is . We should note that from <a href="/the-division-algorithm">The Division Algorithm</a> that the remainder when an integer is divided by satisfies the inequality . Therefore we note that for all nonnegative integers and positive integers that:
In other words, for all nonnegative integers and positive integers , the set of possible remainders when is divided by is .
Consequentially, we can define the set of odd integers and the set of even numbers in terms of these elements in the set of even integers being congruent to one another and elements in the set of odd numbers being congruent to one another.
Definition: An integer is said to be Odd if or Even if .
We will now look at some basic theorems regarding integer congruence modulo .
Theorem 1: Let . Then:
a) If then .
b) .
c) If and then .
d) If and then .
e) If and then .
- Proof of a) Suppose that . Then so there exists an integer such that:
- Therefore so .
- We have that for any integer . Therefore .
- Proof of c) Suppose that and . Then and and there exists integers and such that:
- From the second equation we have that . Substituting this into the first equation gives us:
- Therefore so .
- Proof of d): Suppose that and . Then and , so there exists integers and such that:
- Adding these equations together gives us:
- Therefore so
- Proof of e): Suppose that and . Then and , so there exists integers and such that:
- Multiplying these equations together yields:
- Therefore so .
Algebra on
Let . Since the relation of congruence modulo n is an equivalence relation on , we can discuss its equivalence classes. Recall that in this situation, we refer to the equivalence classes as congruence classes.
Definition of the integers modulo : Let . The set of congruence classes for the relation of congruence modulo on is the set of integers modulo , or the set of integers mod . We will denote this set of congruence classes by .
.
In addition, we know that each integer is congruent to precisely one of the integers 0, 1, 2, ..., . This tells us that one way to represent is
.
Consequently, even though each integer has a congruence class, the set has only distinct congruence classes.
The set of integers is more than a set. We can add and multiply integers. That is, there are the arithmetic operations of addition and multiplication on the set , and we know that is closed with respect to these two operations.
One of the basic problems dealt with in modern algebra is to determine if the arithmetic operations on one set “transfer” to a related set. In this case, the related set is . For example, in the integers modulo 5, , is it possible to add the congruence classes [4] and [2] as follows?
We have used the symbol ̊ to denote addition in so that we do not confuse it with addition in . This looks simple enough, but there is a problem. The congruence classes [4] and [2] are not numbers, they are infinite sets. We have to make sure that we get the same answer no matter what element of [4] we use and no matter what element of [2] we use. For example,
(mod 5) and so [9] = [4]. Also,
(mod 5) and so [7] = [2].
Do we get the same result if we add [9] and [7] in the way we did when we added [4] and [2]? The following computation confirms that we do:
The left side shows the properties in terms of the congruence relation and the right side shows the properties in terms of the congruence classes.
|
If (mod 6) and (mod 6), then
|
If and in , then
|
These are illustrations of general properties that we have already proved in Theorem 3.28. We repeat the statement of the theorem here because it is so important for defining the operations of addition and multiplication in .
Let be a natural number and let , , , and be integers. Then
- If (mod ) and (mod ), then (mod ).
- If (mod ) and (mod ), then (mod ).
- If (mod ) and , then (mod ).
Since (mod ) if and only if , we can restate the result of this Theorem 3.28 in terms of congruence classes in .
Let be a natural number and let , , , and be integers. Then, in .
- If and , then .
- If and , then .
- If and , then .
Now, we know that the following formal definition of addition and multiplication of congruence classes in is independent of the choice of the elements we choose from each class. We say that these definitions of addition and multiplication are well defined.
GCD, LCM, and Bézout's identity
Greatest Common Divisor
Definition: If then the Greatest Common Divisor of and denoted or is an integer such that:
1. and .
2. If , , and then .
Note that the number has the property such that and for all and so we see that the greatest common divisor of any two integers is always at least . As a result, we only need to compare positive divisors of and . Furthermore, if then it's not hard to verify that .
Let's look at an example of finding the greatest common divisor among two integers .
Consider the integers and . The factors of are and the factors of are . Both and share the factor and it is the largest factor they share, and so:
As we elaborated on just moments ago, the greatest common divisor of any two integers is always at least . We give a special name to pairs of integers for which their greatest common divisor is which we define below.
Definition: If and then and are said to be Relatively Prime to each other.
For example, consider the numbers and . The greatest common divisor between these numbers is:
Therefore and are relatively prime to each other.
Theorem 1: If , , and then .
Lowest Common Multiple
For all , there exists a smallest such that and .
This is called the lowest common multiple of and , and denoted .
Finding GCD and LCM with Prime Decomposition
Let .
Let:
- .
That is, the primes given in these prime decompositions may be divisors of either of the numbers or .
Note that if one of the primes does not appear in the prime decompositions of either one of or , then its corresponding index or will be zero.
Then the following results apply:
Bézout's Identity
Let a and b be integers with greatest common divisor d. Then there exist integers x and y such that ax + by = d. More generally, the integers of the form ax + by are exactly the multiples of d.
Proof
Given any nonzero integers a and b, let The set S is nonempty since it contains either a or –a (with x = ±1 and y = 0). Since S is a nonempty set of positive integers, it has a minimum element , by the Well-ordering principle. To prove that d is the greatest common divisor of a and b, it must be proven that d is a common divisor of a and b, and that for any other common divisor c, one has c ≤ d.
The Euclidean division of a by d may be written
The remainder r is in , because
Thus r is of the form , and hence . However, 0 ≤ r < d, and d is the smallest positive integer in S: the remainder r can therefore not be in S, making r necessarily 0. This implies that d is a divisor of a. Similarly d is also a divisor of b, and d is a common divisor of a and b.
Now, let c be any common divisor of a and b; that is, there exist u and v such that a = cu and b = cv. One has thus
That is c is a divisor of d, and, therefore c ≤ d.
Primes
Recall that an integer is a prime number if the only divisors of are and , and an integer that is not a prime number is called a composite number.
We will now look at a very famous, simple, and important theorem which states that there exists infinitely many primes.
| Theorem 1 (Euclid's Theorem of the Existence of Infinitely Many Primes): There are infinitely many prime numbers. |
- Proof: We will carry this proof out by contradiction. Suppose that instead there are a finite number of primes. Then we can list all of these primes:
- Consider the number . We have already seen that every integer has a prime divisor. Let this divisor be for some . Then and . But this implies that which is a contradiction since all and the only divisors of are .
- Therefore the assumption that there were finitely many primes was false and so there are infinitely many primes.
Euclid's Lemma
Euclid's lemma: If a prime p divides the product ab of two integers a and b, then p must divide at least one of those integers a and b.
For example, if p 19, a 133, b 143, then ab 133 × 143 19019, and since this is divisible by 19, the lemma implies that one or both of 133 or 143 must be as well. In fact, 133 19 × 7.
A common proof of Euclid's lemma involves the Bézout's identity, which was unknown at Euclid's time. Bézout's identity states that if x and y are relatively prime integers (i.e. they share no common divisors other than 1 and -1) there exist integers r and s such that
Let a and n be relatively prime, and assume that n ab. By Bézout's identity, there are r and s making
Multiply both sides by b:
The first term on the left is divisible by n, and the second term is divisible by ab, which by hypothesis is divisible by n. Therefore their sum, b, is also divisible by n. This is the generalization of Euclid's lemma mentioned above.
Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic, also known as the Unique Prime Factorization theorem, is as follows:
Theorem 1 (The Unique Prime Factorization Theorem): If and then can be written as a product of primes uniquely apart from the ordering of the primes in the product ( for unique primes ).
If and then can also be written as a product of primes multiplied by .
- Proof: We first show that if and then can be written as a product of primes. We saw on the <a href="/prime-and-composite-numbers">Prime and Composite Numbers</a> page that if every and is divisible by a prime number. Let be this prime number. Then for some we have that:
- If then and we're done. If is prime then let and so and we're done. If is composite then and so once again, is divisible by a prime, say , where . Therefore:
- If then and we're done. If is prime then let and so and we're done. If is composite then and again, is divisible by a prime, say , where .
- Note that . This sequence of integers is bounded below by and hence must terminate at some point. Therefore, for some we have that:
- Therefore can be written as a product of primes. We will now show that this factorization is unique. Suppose that and so that then:
- Since we must have . Therefore for some . Without loss of generality, assume that . Therefore:
- Since we must also have . Therefore for some . Without loss of generality, assume that . Therefore:
- We continue in this process. We note that we won't run out of primes before primes , otherwise this implies a prime is equal to . Furthermore, we won't run out of primes before primes , otherwise this implies a prime is equal to . Therefore and we eventually get:
- Therefore the prime factorization is unique.
Licensing
Content obtained and/or adapted from:
- Natural number, Wikipedia under a CC BY-SA license
- Integer, Wikipedia under a CC BY-SA license
- Mathematical induction, Wikipedia under a CC BY-SA license
- Euclid's lemma, Wikipedia under a CC BY-SA license
- Prime number, Wikipedia under a CC BY-SA license
- Abstract Algebra, mathonline.wikidot.com under a CC BY-SA license
- Modular Arithmetic, LibreTexts: Mathematics under a CC BY-SA license





















































![{\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ada63de55374aa09013be65caa1c33aa0164ecb3)
![{\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ea8c51ad5f2968fcf5788eb220d4f4463b28588)
![{\displaystyle -[(a,b)]:=[(b,a)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/951d0171ed1edf705e70392352f3d07b94ed4c74)
![{\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef8af489c7cff40fe4cfe66d5a706837fc0a6df6)
![{\displaystyle [(a,b)]<[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5f5d9d3f2ef39e8cf90692589f0b97945454536)


![{\displaystyle {\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/325c6a83a84e4fe08bac03e453f674b1ff83eac1)

























































































![{\displaystyle \mathbb {Z} =[0]\cup [1]\cup [2]\cup \cdot \cdot \cdot \cup [n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8bda09b390d46269f13d399749887b987313ce4)

![{\displaystyle \mathbb {Z} _{n}=\{[0],[1],[2],...[n-1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53239e5d3da2dd3d4a07fba90a5e9d9b04605212)

![{\displaystyle {\begin{array}{rcl}{[4]\oplus [2]}&=&{[4+2]}\\{}&=&{[6]}\\{}&=&{[1].}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf0787980dbf547e85a2a8b774ac9c527c937dcc)


![{\displaystyle {\begin{array}{rcl}{[9]\oplus [7]}&=&{[9+7]}\\{}&=&{[16]}\\{}&=&{[1].}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b7ee3558c56df6d89a8c9ae5780daf1389811ae)




![{\displaystyle [a]=[3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e88c2c3c24ea9de1f8be4c70d7ec0c49eba6a4fb)
![{\displaystyle [b]=[4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f06238b5c0feae4ad4757d766ce3362950bb9c1)

![{\displaystyle [a+b]=[3+4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/990185c884a73ee973298bd2d4c22772f7ffab42)
![{\displaystyle [a\cdot b]=[3\cdot 4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bdb86da38f5a6d50a48adab022804fc6dc316be)









![{\displaystyle [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a)
![{\displaystyle [a]=[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/410d2187c04d4e54d4ccec24556a76fd427a93aa)
![{\displaystyle [c]=[d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2edfa99d27353e231deedbe9ff4aab563d9c8fa9)
![{\displaystyle [a+c]=[b+d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19b2c98aa9cf6b7e2ad46ad8eb5ff501a1fe6401)
![{\displaystyle [a\cdot c]=[b\cdot d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b94cc0617b509524bc85c04a7b5c2178325c2d)
![{\displaystyle [a]^{m}=[b]^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2bb1905338404c4c57bda102dac219e7876974a)










































































































