Base 10, Base 2 & Base 5
In a positional numeral system, the radix or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal/denary system (the most common system in use today) the radix (base number) is ten, because it uses the ten digits from 0 through 9.
In any standard positional numeral system, a number is conventionally written as (x)y with x as the string of digits and y as its base, although for base ten the subscript is usually assumed (and omitted, together with the pair of parentheses), as it is the most common way to express value. For example, (100)10 is equivalent to 100 (the decimal system is implied in the latter) and represents the number one hundred, while (100)2 (in the binary system with base 2) represents the number four.
Contents
In numeral systems
In the system with radix 13, for example, a string of digits such as 398 denotes the (decimal) number 3 × 132 + 9 × 131 + 8 × 130 = 632.
More generally, in a system with radix b (b > 1), a string of digits d1 … dn denotes the number d1bn−1 + d2bn−2 + … + dnb0, where 0 ≤ di < b. In contrast to decimal, or radix 10, which has a ones' place, tens' place, hundreds' place, and so on, radix b would have a ones' place, then a b1s' place, a b2s' place, etc.
Commonly used numeral systems include:
| Base/radix | Name | Description |
|---|---|---|
| 2 | Binary numeral system | Used internally by nearly all computers, is base 2. The two digits are "0" and "1", expressed from switches displaying OFF and ON, respectively. Used in most electric counters. |
| 8 | Octal system | Used occasionally in computing. The eight digits are "0"–"7" and represent 3 bits (23). |
| 10 | Decimal system | Used by humans in the vast majority of cultures. Its ten digits are "0"–"9". Used in most mechanical counters. |
| 12 | Duodecimal (dozenal) system | Sometimes advocated due to divisibility by 2, 3, 4, and 6. It was traditionally used as part of quantities expressed in dozens and grosses. |
| 16 | Hexadecimal system | Often used in computing as a more compact representation of binary (1 hex digit per 4 bits). The sixteen digits are "0"–"9" followed by "A"–"F" or "a"–"f". |
| 20 | Vigesimal system | Traditional numeral system in several cultures, still used by some for counting. Historically also known as the score system in English, now most famous in the phrase "four score and seven years ago" in the Gettysburg Address. |
| 60 | Sexagesimal system | Originated in ancient Sumer and passed to the Babylonians. Used today as the basis of modern circular coordinate system (degrees, minutes, and seconds) and time measuring (minutes, and seconds) by analogy to the rotation of the Earth. |
Base 2
A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method of mathematical expression which uses only two symbols: typically "0" (zero) and "1" (one).
The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language.
Representation
Any number can be represented by a sequence of bits (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states. Any of the following rows of symbols can be interpreted as the binary numeric value of 667:
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| | | ― | | | ― | ― | | | | | ― | | | | |
| ☒ | ☐ | ☒ | ☐ | ☐ | ☒ | ☒ | ☐ | ☒ | ☒ |
| y | n | y | n | n | y | y | n | y | y |
The numeric value represented in each case is dependent upon the value assigned to each symbol. In the earlier days of computing, switches, punched holes and punched paper tapes were used to represent binary values. In a modern computer, the numeric values may be represented by two different voltages; on a magnetic disk, magnetic polarities may be used. A "positive", "yes", or "on" state is not necessarily equivalent to the numerical value of one; it depends on the architecture in use.
In keeping with customary representation of numerals using Arabic numerals, binary numbers are commonly written using the symbols 0 and 1. When written, binary numerals are often subscripted, prefixed or suffixed in order to indicate their base, or radix. The following notations are equivalent:
- 100101 binary (explicit statement of format)
- 100101b (a suffix indicating binary format; also known as Intel convention)
- 100101B (a suffix indicating binary format)
- bin 100101 (a prefix indicating binary format)
- 1001012 (a subscript indicating base-2 (binary) notation)
- %100101 (a prefix indicating binary format; also known as Motorola convention)
- 0b100101 (a prefix indicating binary format, common in programming languages)
- 6b100101 (a prefix indicating number of bits in binary format, common in programming languages)
- #b100101 (a prefix indicating binary format, common in Lisp programming languages)
When spoken, binary numerals are usually read digit-by-digit, in order to distinguish them from decimal numerals. For example, the binary numeral 100 is pronounced one zero zero, rather than one hundred, to make its binary nature explicit, and for purposes of correctness. Since the binary numeral 100 represents the value four, it would be confusing to refer to the numeral as one hundred (a word that represents a completely different value, or amount). Alternatively, the binary numeral 100 can be read out as "four" (the correct value), but this does not make its binary nature explicit.
Counting in binary
Counting in binary is similar to counting in any other number system. Beginning with a single digit, counting proceeds through each symbol, in increasing order. Before examining binary counting, it is useful to briefly discuss the more familiar decimal counting system as a frame of reference.
Decimal counting
Decimal counting uses the ten symbols 0 through 9. Counting begins with the incremental substitution of the least significant digit (rightmost digit) which is often called the first digit. When the available symbols for this position are exhausted, the least significant digit is reset to 0, and the next digit of higher significance (one position to the left) is incremented (overflow), and incremental substitution of the low-order digit resumes. This method of reset and overflow is repeated for each digit of significance. Counting progresses as follows:
- 000, 001, 002, ... 007, 008, 009, (rightmost digit is reset to zero, and the digit to its left is incremented)
- 010, 011, 012, ...
- ...
- 090, 091, 092, ... 097, 098, 099, (rightmost two digits are reset to zeroes, and next digit is incremented)
- 100, 101, 102, ...
Binary counting
Binary counting follows the same procedure, except that only the two symbols 0 and 1 are available. Thus, after a digit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next digit to the left:
- 0000,
- 0001, (rightmost digit starts over, and next digit is incremented)
- 0010, 0011, (rightmost two digits start over, and next digit is incremented)
- 0100, 0101, 0110, 0111, (rightmost three digits start over, and the next digit is incremented)
- 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...
In the binary system, each digit represents an increasing power of 2, with the rightmost digit representing 20, the next representing 21, then 22, and so on. The value of a binary number is the sum of the powers of 2 represented by each "1" digit. For example, the binary number 100101 is converted to decimal form as follows:
- 1001012 = [ ( 1 ) × 25 ] + [ ( 0 ) × 24 ] + [ ( 0 ) × 23 ] + [ ( 1 ) × 22 ] + [ ( 0 ) × 21 ] + [ ( 1 ) × 20 ]
- 1001012 = [ 1 × 32 ] + [ 0 × 16 ] + [ 0 × 8 ] + [ 1 × 4 ] + [ 0 × 2 ] + [ 1 × 1 ]
- 1001012 = 3710
Fractions
Fractions in binary arithmetic terminate only if 2 is the only prime factor in the denominator. As a result, 1/10 does not have a finite binary representation (10 has prime factors 2 and 5). This causes 10 × 0.1 not to precisely equal 1 in floating-point arithmetic. As an example, to interpret the binary expression for 1/3 = .010101..., this means: 1/3 = 0 × 2−1 + 1 × 2−2 + 0 × 2−3 + 1 × 2−4 + ... = 0.3125 + ... An exact value cannot be found with a sum of a finite number of inverse powers of two, the zeros and ones in the binary representation of 1/3 alternate forever.
| Fraction | Decimal | Binary | Fractional approximation |
|---|---|---|---|
| 1/1 | 1 or 0.999... | 1 or 0.111... | 1/2 + 1/4 + 1/8... |
| 1/2 | 0.5 or 0.4999... | 0.1 or 0.0111... | 1/4 + 1/8 + 1/16 . . . |
| 1/3 | 0.333... | 0.010101... | 1/4 + 1/16 + 1/64 . . . |
| 1/4 | 0.25 or 0.24999... | 0.01 or 0.00111... | 1/8 + 1/16 + 1/32 . . . |
| 1/5 | 0.2 or 0.1999... | 0.00110011... | 1/8 + 1/16 + 1/128 . . . |
| 1/6 | 0.1666... | 0.0010101... | 1/8 + 1/32 + 1/128 . . . |
| 1/7 | 0.142857142857... | 0.001001... | 1/8 + 1/64 + 1/512 . . . |
| 1/8 | 0.125 or 0.124999... | 0.001 or 0.000111... | 1/16 + 1/32 + 1/64 . . . |
| 1/9 | 0.111... | 0.000111000111... | 1/16 + 1/32 + 1/64 . . . |
| 1/10 | 0.1 or 0.0999... | 0.000110011... | 1/16 + 1/32 + 1/256 . . . |
| 1/11 | 0.090909... | 0.00010111010001011101... | 1/16 + 1/64 + 1/128 . . . |
| 1/12 | 0.08333... | 0.00010101... | 1/16 + 1/64 + 1/256 . . . |
| 1/13 | 0.076923076923... | 0.000100111011000100111011... | 1/16 + 1/128 + 1/256 . . . |
| 1/14 | 0.0714285714285... | 0.0001001001... | 1/16 + 1/128 + 1/1024 . . . |
| 1/15 | 0.0666... | 0.00010001... | 1/16 + 1/256 . . . |
| 1/16 | 0.0625 or 0.0624999... | 0.0001 or 0.0000111... | 1/32 + 1/64 + 1/128 . . . |
Binary arithmetic
Arithmetic in binary is much like arithmetic in other numeral systems. Addition, subtraction, multiplication, and division can be performed on binary numerals.
Addition
The simplest arithmetic operation in binary is addition. Adding two single-digit binary numbers is relatively simple, using a form of carrying:
- 0 + 0 → 0
- 0 + 1 → 1
- 1 + 0 → 1
- 1 + 1 → 0, carry 1 (since 1 + 1 = 2 = 0 + (1 × 21) )
Adding two "1" digits produces a digit "0", while 1 will have to be added to the next column. This is similar to what happens in decimal when certain single-digit numbers are added together; if the result equals or exceeds the value of the radix (10), the digit to the left is incremented:
- 5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 101) )
- 7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 101) )
This is known as carrying. When the result of an addition exceeds the value of a digit, the procedure is to "carry" the excess amount divided by the radix (that is, 10/10) to the left, adding it to the next positional value. This is correct since the next position has a weight that is higher by a factor equal to the radix. Carrying works the same way in binary:
1 1 1 1 1 (carried digits)
0 1 1 0 1
+ 1 0 1 1 1
-------------
= 1 0 0 1 0 0 = 36
In this example, two numerals are being added together: 011012 (1310) and 101112 (2310). The top row shows the carry bits used. Starting in the rightmost column, 1 + 1 = 102. The 1 is carried to the left, and the 0 is written at the bottom of the rightmost column. The second column from the right is added: 1 + 0 + 1 = 102 again; the 1 is carried, and 0 is written at the bottom. The third column: 1 + 1 + 1 = 112. This time, a 1 is carried, and a 1 is written in the bottom row. Proceeding like this gives the final answer 1001002 (3610).
When computers must add two numbers, the rule that: x xor y = (x + y) mod 2 for any two bits x and y allows for very fast calculation, as well.
Long carry method
A simplification for many binary addition problems is the Long Carry Method or Brookhouse Method of Binary Addition. This method is generally useful in any binary addition in which one of the numbers contains a long "string" of ones. It is based on the simple premise that under the binary system, when given a "string" of digits composed entirely of n ones (where n is any integer length), adding 1 will result in the number 1 followed by a string of n zeros. That concept follows, logically, just as in the decimal system, where adding 1 to a string of n 9s will result in the number 1 followed by a string of n 0s:
Binary Decimal
1 1 1 1 1 likewise 9 9 9 9 9
+ 1 + 1
——————————— ———————————
1 0 0 0 0 0 1 0 0 0 0 0
Such long strings are quite common in the binary system. From that one finds that large binary numbers can be added using two simple steps, without excessive carry operations. In the following example, two numerals are being added together: 1 1 1 0 1 1 1 1 1 02 (95810) and 1 0 1 0 1 1 0 0 1 12 (69110), using the traditional carry method on the left, and the long carry method on the right:
Traditional Carry Method Long Carry Method
vs.
1 1 1 1 1 1 1 1 (carried digits) 1 ← 1 ← carry the 1 until it is one digit past the "string" below
1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 0 cross out the "string",
+ 1 0 1 0 1 1 0 0 1 1 + 1 0 1 0 1 1 0 0 1 1 and cross out the digit that was added to it
——————————————————————— ——————————————————————
= 1 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1
The top row shows the carry bits used. Instead of the standard carry from one column to the next, the lowest-ordered "1" with a "1" in the corresponding place value beneath it may be added and a "1" may be carried to one digit past the end of the series. The "used" numbers must be crossed off, since they are already added. Other long strings may likewise be cancelled using the same technique. Then, simply add together any remaining digits normally. Proceeding in this manner gives the final answer of 1 1 0 0 1 1 1 0 0 0 12 (164910). In our simple example using small numbers, the traditional carry method required eight carry operations, yet the long carry method required only two, representing a substantial reduction of effort.
Addition table
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10 |
The binary addition table is similar, but not the same, as the truth table of the logical disjunction operation . The difference is that , while .
Subtraction
Subtraction works in much the same way:
- 0 − 0 → 0
- 0 − 1 → 1, borrow 1
- 1 − 0 → 1
- 1 − 1 → 0
Subtracting a "1" digit from a "0" digit produces the digit "1", while 1 will have to be subtracted from the next column. This is known as borrowing. The principle is the same as for carrying. When the result of a subtraction is less than 0, the least possible value of a digit, the procedure is to "borrow" the deficit divided by the radix (that is, 10/10) from the left, subtracting it from the next positional value.
* * * * (starred columns are borrowed from) 1 1 0 1 1 1 0 − 1 0 1 1 1 ---------------- = 1 0 1 0 1 1 1
* (starred columns are borrowed from) 1 0 1 1 1 1 1 - 1 0 1 0 1 1 ---------------- = 0 1 1 0 1 0 0
Subtracting a positive number is equivalent to adding a negative number of equal absolute value. Computers use signed number representations to handle negative numbers—most commonly the two's complement notation. Such representations eliminate the need for a separate "subtract" operation. Using two's complement notation subtraction can be summarized by the following formula:
- A − B = A + not B + 1
Multiplication
Multiplication in binary is similar to its decimal counterpart. Two numbers A and B can be multiplied by partial products: for each digit in B, the product of that digit in A is calculated and written on a new line, shifted leftward so that its rightmost digit lines up with the digit in B that was used. The sum of all these partial products gives the final result.
Since there are only two digits in binary, there are only two possible outcomes of each partial multiplication:
- If the digit in B is 0, the partial product is also 0
- If the digit in B is 1, the partial product is equal to A
For example, the binary numbers 1011 and 1010 are multiplied as follows:
1 0 1 1 (A)
× 1 0 1 0 (B)
---------
0 0 0 0 ← Corresponds to the rightmost 'zero' in B
+ 1 0 1 1 ← Corresponds to the next 'one' in B
+ 0 0 0 0
+ 1 0 1 1
---------------
= 1 1 0 1 1 1 0
Binary numbers can also be multiplied with bits after a binary point:
1 0 1 . 1 0 1 A (5.625 in decimal)
× 1 1 0 . 0 1 B (6.25 in decimal)
-------------------
1 . 0 1 1 0 1 ← Corresponds to a 'one' in B
+ 0 0 . 0 0 0 0 ← Corresponds to a 'zero' in B
+ 0 0 0 . 0 0 0
+ 1 0 1 1 . 0 1
+ 1 0 1 1 0 . 1
---------------------------
= 1 0 0 0 1 1 . 0 0 1 0 1 (35.15625 in decimal)
See also Booth's multiplication algorithm.
Multiplication table
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
The binary multiplication table is the same as the truth table of the logical conjunction operation .
Division
Long division in binary is again similar to its decimal counterpart.
In the example below, the divisor is 1012, or 5 in decimal, while the dividend is 110112, or 27 in decimal. The procedure is the same as that of decimal long division; here, the divisor 1012 goes into the first three digits 1102 of the dividend one time, so a "1" is written on the top line. This result is multiplied by the divisor, and subtracted from the first three digits of the dividend; the next digit (a "1") is included to obtain a new three-digit sequence:
1
___________
1 0 1 ) 1 1 0 1 1
− 1 0 1
-----
0 0 1
The procedure is then repeated with the new sequence, continuing until the digits in the dividend have been exhausted:
1 0 1
___________
1 0 1 ) 1 1 0 1 1
− 1 0 1
-----
1 1 1
− 1 0 1
-----
0 1 0
Thus, the quotient of 110112 divided by 1012 is 1012, as shown on the top line, while the remainder, shown on the bottom line, is 102. In decimal, this corresponds to the fact that 27 divided by 5 is 5, with a remainder of 2.
Aside from long division, one can also devise the procedure so as to allow for over-subtracting from the partial remainder at each iteration, thereby leading to alternative methods which are less systematic, but more flexible as a result.
Square root
The process of taking a binary square root digit by digit is the same as for a decimal square root and is explained here. An example is:
1 0 0 1
---------
√ 1010001
1
---------
101 01
0
--------
1001 100
0
--------
10001 10001
10001
-------
0
Conversion to and from other numeral systems
Decimal to Binary
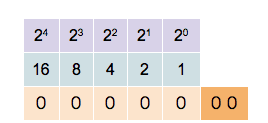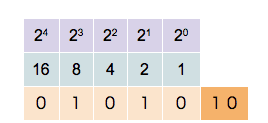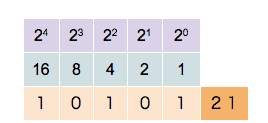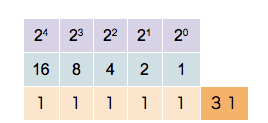
To convert from a base-10 integer to its base-2 (binary) equivalent, the number is divided by two. The remainder is the least-significant bit. The quotient is again divided by two; its remainder becomes the next least significant bit. This process repeats until a quotient of one is reached. The sequence of remainders (including the final quotient of one) forms the binary value, as each remainder must be either zero or one when dividing by two. For example, (357)10 is expressed as (101100101)2.
Binary to Decimal
Conversion from base-2 to base-10 simply inverts the preceding algorithm. The bits of the binary number are used one by one, starting with the most significant (leftmost) bit. Beginning with the value 0, the prior value is doubled, and the next bit is then added to produce the next value. This can be organized in a multi-column table. For example, to convert 100101011012 to decimal:
| Prior value | × 2 + | Next bit | Next value |
|---|---|---|---|
| 0 | × 2 + | 1 | = 1 |
| 1 | × 2 + | 0 | = 2 |
| 2 | × 2 + | 0 | = 4 |
| 4 | × 2 + | 1 | = 9 |
| 9 | × 2 + | 0 | = 18 |
| 18 | × 2 + | 1 | = 37 |
| 37 | × 2 + | 0 | = 74 |
| 74 | × 2 + | 1 | = 149 |
| 149 | × 2 + | 1 | = 299 |
| 299 | × 2 + | 0 | = 598 |
| 598 | × 2 + | 1 | = 1197 |
The result is 119710. The first Prior Value of 0 is simply an initial decimal value. This method is an application of the Horner scheme.
| Binary | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Decimal | 1×210 + | 0×29 + | 0×28 + | 1×27 + | 0×26 + | 1×25 + | 0×24 + | 1×23 + | 1×22 + | 0×21 + | 1×20 = | 1197 |
The fractional parts of a number are converted with similar methods. They are again based on the equivalence of shifting with doubling or halving.
In a fractional binary number such as 0.110101101012, the first digit is , the second , etc. So if there is a 1 in the first place after the decimal, then the number is at least , and vice versa. Double that number is at least 1. This suggests the algorithm: Repeatedly double the number to be converted, record if the result is at least 1, and then throw away the integer part.
For example, 10, in binary, is:
| Converting | Result |
|---|---|
| 0. | |
| 0.0 | |
| 0.01 | |
| 0.010 | |
| 0.0101 |
Thus the repeating decimal fraction ... is equivalent to the repeating binary fraction ... .
Or for example, 0.110, in binary, is:
| Converting | Result |
|---|---|
| 0.1 | 0. |
| 0.1 × 2 = 0.2 < 1 | 0.0 |
| 0.2 × 2 = 0.4 < 1 | 0.00 |
| 0.4 × 2 = 0.8 < 1 | 0.000 |
| 0.8 × 2 = 1.6 ≥ 1 | 0.0001 |
| 0.6 × 2 = 1.2 ≥ 1 | 0.00011 |
| 0.2 × 2 = 0.4 < 1 | 0.000110 |
| 0.4 × 2 = 0.8 < 1 | 0.0001100 |
| 0.8 × 2 = 1.6 ≥ 1 | 0.00011001 |
| 0.6 × 2 = 1.2 ≥ 1 | 0.000110011 |
| 0.2 × 2 = 0.4 < 1 | 0.0001100110 |
This is also a repeating binary fraction ... . It may come as a surprise that terminating decimal fractions can have repeating expansions in binary. It is for this reason that many are surprised to discover that 0.1 + ... + 0.1, (10 additions) differs from 1 in floating point arithmetic. In fact, the only binary fractions with terminating expansions are of the form of an integer divided by a power of 2, which 1/10 is not.
The final conversion is from binary to decimal fractions. The only difficulty arises with repeating fractions, but otherwise the method is to shift the fraction to an integer, convert it as above, and then divide by the appropriate power of two in the decimal base. For example:
Another way of converting from binary to decimal, often quicker for a person familiar with hexadecimal, is to do so indirectly—first converting ( in binary) into ( in hexadecimal) and then converting ( in hexadecimal) into ( in decimal).
For very large numbers, these simple methods are inefficient because they perform a large number of multiplications or divisions where one operand is very large. A simple divide-and-conquer algorithm is more effective asymptotically: given a binary number, it is divided by 10k, where k is chosen so that the quotient roughly equals the remainder; then each of these pieces is converted to decimal and the two are concatenated. Given a decimal number, it can be split into two pieces of about the same size, each of which is converted to binary, whereupon the first converted piece is multiplied by 10k and added to the second converted piece, where k is the number of decimal digits in the second, least-significant piece before conversion.
Hexadecimal
Binary may be converted to and from hexadecimal more easily. This is because the radix of the hexadecimal system (16) is a power of the radix of the binary system (2). More specifically, 16 = 24, so it takes four digits of binary to represent one digit of hexadecimal, as shown in the adjacent table.
To convert a hexadecimal number into its binary equivalent, simply substitute the corresponding binary digits:
- 3A16 = 0011 10102
- E716 = 1110 01112
To convert a binary number into its hexadecimal equivalent, divide it into groups of four bits. If the number of bits isn't a multiple of four, simply insert extra 0 bits at the left (called padding). For example:
- 10100102 = 0101 0010 grouped with padding = 5216
- 110111012 = 1101 1101 grouped = DD16
To convert a hexadecimal number into its decimal equivalent, multiply the decimal equivalent of each hexadecimal digit by the corresponding power of 16 and add the resulting values:
- C0E716 = (12 × 163) + (0 × 162) + (14 × 161) + (7 × 160) = (12 × 4096) + (0 × 256) + (14 × 16) + (7 × 1) = 49,38310
Octal
Binary is also easily converted to the octal numeral system, since octal uses a radix of 8, which is a power of two (namely, 23, so it takes exactly three binary digits to represent an octal digit). The correspondence between octal and binary numerals is the same as for the first eight digits of hexadecimal in the table above. Binary 000 is equivalent to the octal digit 0, binary 111 is equivalent to octal 7, and so forth.
| Octal | Binary |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Converting from octal to binary proceeds in the same fashion as it does for hexadecimal:
- 658 = 110 1012
- 178 = 001 1112
And from binary to octal:
- 1011002 = 101 1002 grouped = 548
- 100112 = 010 0112 grouped with padding = 238
And from octal to decimal:
- 658 = (6 × 81) + (5 × 80) = (6 × 8) + (5 × 1) = 5310
- 1278 = (1 × 82) + (2 × 81) + (7 × 80) = (1 × 64) + (2 × 8) + (7 × 1) = 8710
Representing real numbers
Non-integers can be represented by using negative powers, which are set off from the other digits by means of a radix point (called a decimal point in the decimal system). For example, the binary number 11.012 means:
| 1 × 21 | (1 × 2 = 2) | plus |
| 1 × 20 | (1 × 1 = 1) | plus |
| 0 × 2−1 | (0 × = 0) | plus |
| 1 × 2−2 | (1 × = 0.25) |
For a total of 3.25 decimal.
All dyadic rational numbers have a terminating binary numeral—the binary representation has a finite number of terms after the radix point. Other rational numbers have binary representation, but instead of terminating, they recur, with a finite sequence of digits repeating indefinitely. For instance
The phenomenon that the binary representation of any rational is either terminating or recurring also occurs in other radix-based numeral systems. See, for instance, the explanation in decimal. Another similarity is the existence of alternative representations for any terminating representation, relying on the fact that 0.111111... is the sum of the geometric series 2−1 + 2−2 + 2−3 + ... which is 1.
Binary numerals which neither terminate nor recur represent irrational numbers. For instance,
- 0.10100100010000100000100... does have a pattern, but it is not a fixed-length recurring pattern, so the number is irrational
- 1.0110101000001001111001100110011111110... is the binary representation of , the square root of 2, another irrational. It has no discernible pattern.
Base 5
Quinary /ˈkwaɪnəri/ (base-5 or pental) is a numeral system with five as the base. A possible origination of a quinary system is that there are five digits on either hand.
In the quinary place system, five numerals, from 0 to 4, are used to represent any real number. According to this method, five is written as 10, twenty-five is written as 100 and sixty is written as 220.
As five is a prime number, only the reciprocals of the powers of five terminate, although its location between two highly composite numbers (4 and 6) guarantees that many recurring fractions have relatively short periods.
Today, the main usage of base 5 is as a biquinary system, which is decimal using five as a sub-base. Another example of a sub-base system, is sexagesimal, base 60, which used 10 as a sub-base.
Each quinary digit can hold log25 (approx. 2.32) bits of information.
Comparison to other radices
| × | 1 | 2 | 3 | 4 | 10 | 11 | 12 | 13 | 14 | 20 |
| 1 | 1 | 2 | 3 | 4 | 10 | 11 | 12 | 13 | 14 | 20 |
| 2 | 2 | 4 | 11 | 13 | 20 | 22 | 24 | 31 | 33 | 40 |
| 3 | 3 | 11 | 14 | 22 | 30 | 33 | 41 | 44 | 102 | 110 |
| 4 | 4 | 13 | 22 | 31 | 40 | 44 | 103 | 112 | 121 | 130 |
| 10 | 10 | 20 | 30 | 40 | 100 | 110 | 120 | 130 | 140 | 200 |
| 11 | 11 | 22 | 33 | 44 | 110 | 121 | 132 | 143 | 204 | 220 |
| 12 | 12 | 24 | 41 | 103 | 120 | 132 | 144 | 211 | 223 | 240 |
| 13 | 13 | 31 | 44 | 112 | 130 | 143 | 211 | 224 | 242 | 310 |
| 14 | 14 | 33 | 102 | 121 | 140 | 204 | 223 | 242 | 311 | 330 |
| 20 | 20 | 40 | 110 | 130 | 200 | 220 | 240 | 310 | 330 | 400 |
| Quinary | 0 | 1 | 2 | 3 | 4 | 10 | 11 | 12 | 13 | 14 | 20 | 21 | 22 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Binary | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 |
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Quinary | 23 | 24 | 30 | 31 | 32 | 33 | 34 | 40 | 41 | 42 | 43 | 44 | 100 |
| Binary | 1101 | 1110 | 1111 | 10000 | 10001 | 10010 | 10011 | 10100 | 10101 | 10110 | 10111 | 11000 | 11001 |
| Decimal | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Decimal (periodic part) | Quinary (periodic part) | Binary (periodic part) |
| 1/2 = 0.5 | 1/2 = 0.2 | 1/10 = 0.1 |
| 1/3 = 0.3 | 1/3 = 0.13 | 1/11 = 0.01 |
| 1/4 = 0.25 | 1/4 = 0.1 | 1/100 = 0.01 |
| 1/5 = 0.2 | 1/10 = 0.1 | 1/101 = 0.0011 |
| 1/6 = 0.16 | 1/11 = 0.04 | 1/110 = 0.010 |
| 1/7 = 0.142857 | 1/12 = 0.032412 | 1/111 = 0.001 |
| 1/8 = 0.125 | 1/13 = 0.03 | 1/1000 = 0.001 |
| 1/9 = 0.1 | 1/14 = 0.023421 | 1/1001 = 0.000111 |
| 1/10 = 0.1 | 1/20 = 0.02 | 1/1010 = 0.00011 |
| 1/11 = 0.09 | 1/21 = 0.02114 | 1/1011 = 0.0001011101 |
| 1/12 = 0.083 | 1/22 = 0.02 | 1/1100 = 0.0001 |
| 1/13 = 0.076923 | 1/23 = 0.0143 | 1/1101 = 0.000100111011 |
| 1/14 = 0.0714285 | 1/24 = 0.013431 | 1/1110 = 0.0001 |
| 1/15 = 0.06 | 1/30 = 0.013 | 1/1111 = 0.0001 |
| 1/16 = 0.0625 | 1/31 = 0.0124 | 1/10000 = 0.0001 |
| 1/17 = 0.0588235294117647 | 1/32 = 0.0121340243231042 | 1/10001 = 0.00001111 |
| 1/18 = 0.05 | 1/33 = 0.011433 | 1/10010 = 0.0000111 |
| 1/19 = 0.052631578947368421 | 1/34 = 0.011242141 | 1/10011 = 0.000011010111100101 |
| 1/20 = 0.05 | 1/40 = 0.01 | 1/10100 = 0.000011 |
| 1/21 = 0.047619 | 1/41 = 0.010434 | 1/10101 = 0.000011 |
| 1/22 = 0.045 | 1/42 = 0.01032 | 1/10110 = 0.00001011101 |
| 1/23 = 0.0434782608695652173913 | 1/43 = 0.0102041332143424031123 | 1/10111 = 0.00001011001 |
| 1/24 = 0.0416 | 1/44 = 0.01 | 1/11000 = 0.00001 |
| 1/25 = 0.04 | 1/100 = 0.01 | 1/11001 = 0.00001010001111010111 |
Usage
Many languages use quinary number systems, including Gumatj, Nunggubuyu, Kuurn Kopan Noot, Luiseño and Saraveca. Gumatj is a true "5–25" language, in which 25 is the higher group of 5. The Gumatj numerals are shown below:
| Number | Base 5 | Numeral |
|---|---|---|
| 1 | 1 | wanggany |
| 2 | 2 | marrma |
| 3 | 3 | lurrkun |
| 4 | 4 | dambumiriw |
| 5 | 10 | wanggany rulu |
| 10 | 20 | marrma rulu |
| 15 | 30 | lurrkun rulu |
| 20 | 40 | dambumiriw rulu |
| 25 | 100 | dambumirri rulu |
| 50 | 200 | marrma dambumirri rulu |
| 75 | 300 | lurrkun dambumirri rulu |
| 100 | 400 | dambumiriw dambumirri rulu |
| 125 | 1000 | dambumirri dambumirri rulu |
| 625 | 10000 | dambumirri dambumirri dambumirri rulu |
Biquinary
A decimal system with 2 and 5 as a sub-bases is called biquinary, and is found in Wolof and Khmer. Roman numerals are an early biquinary system. The numbers 1, 5, 10, and 50 are written as I, V, X, and L respectively. Seven is VII and seventy is LXX. The full list is:
| I | V | X | L | C | D | M |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Note that these are not positional number systems. In theory a number such as 73 could be written as IIIXXL without ambiguity as well as LXXIII and it is still not possible to extend it beyond thousands. There is also no sign for zero. But with the introduction of inversions such as IV and IX, it was necessary to keep the order from most to least significant.
Many versions of the abacus, such as the suanpan and soroban, use a biquinary system to simulate a decimal system for ease of calculation. Urnfield culture numerals and some tally mark systems are also biquinary. Units of currencies are commonly partially or wholly biquinary.
Bi-quinary coded decimal is a variant of biquinary that was used on a number of early computers including Colossus and the IBM 650 to represent decimal numbers.
Base 10
The decimal numeral system (also called the base-ten positional numeral system, and occasionally called denary /ˈdiːnəri/ or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as decimal notation.
A decimal numeral (also often just decimal or, less correctly, decimal number), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in 25.9703 or 3,1415). Decimal may also refer specifically to the digits after the decimal separator, such as in "3.14 is the approximation of to two decimals". Zero-digits after a decimal separator serve the purpose of signifying the precision of a value.
The numbers that may be represented in the decimal system are the decimal fractions. That is, fractions of the form a/10n, where a is an integer, and n is a non-negative integer.
The decimal system has been extended to infinite decimals for representing any real number, by using an infinite sequence of digits after the decimal separator (see decimal representation). In this context, the decimal numerals with a finite number of non-zero digits after the decimal separator are sometimes called terminating decimals. A repeating decimal is an infinite decimal that, after some place, repeats indefinitely the same sequence of digits (e.g., 5.123144144144144... = ). An infinite decimal represents a rational number, the quotient of two integers, if and only if it is a repeating decimal or has a finite number of non-zero digits.
Origin
Many numeral systems of ancient civilizations use ten and its powers for representing numbers, possibly because there are ten fingers on two hands and people started counting by using their fingers. Examples are firstly the Egyptian numerals, then the Brahmi numerals, Greek numerals, Hebrew numerals, Roman numerals, and Chinese numerals. Very large numbers were difficult to represent in these old numeral systems, and only the best mathematicians were able to multiply or divide large numbers. These difficulties were completely solved with the introduction of the Hindu–Arabic numeral system for representing integers. This system has been extended to represent some non-integer numbers, called decimal fractions or decimal numbers, for forming the decimal numeral system.
Decimal notation
For writing numbers, the decimal system uses ten decimal digits, a decimal mark, and, for negative numbers, a minus sign "−". The decimal digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; and a comma "," in other countries.
For representing a non-negative number, a decimal numeral consists of
- either a (finite) sequence of digits (such as "2017"), where the entire sequence represents an integer,
- or a decimal mark separating two sequences of digits (such as "20.70828")
- .
If m > 0, that is, if the first sequence contains at least two digits, it is generally assumed that the first digit am is not zero. In some circumstances it may be useful to have one or more 0's on the left; this does not change the value represented by the decimal: for example, 3.14 = 03.14 = 003.14. Similarly, if the final digit on the right of the decimal mark is zero—that is, if bn = 0—it may be removed; conversely, trailing zeros may be added after the decimal mark without changing the represented number; for example, 15 = 15.0 = 15.00 and 5.2 = 5.20 = 5.200.
For representing a negative number, a minus sign is placed before am.
The numeral represents the number
- .
The integer part or integral part of a decimal numeral is the integer written to the left of the decimal separator (see also truncation). For a non-negative decimal numeral, it is the largest integer that is not greater than the decimal. The part from the decimal separator to the right is the fractional part, which equals the difference between the numeral and its integer part.
When the integral part of a numeral is zero, it may occur, typically in computing, that the integer part is not written (for example .1234, instead of 0.1234). In normal writing, this is generally avoided, because of the risk of confusion between the decimal mark and other punctuation.
In brief, the contribution of each digit to the value of a number depends on its position in the numeral. That is, the decimal system is a positional numeral system.
Decimal fractions
Decimal fractions (sometimes called decimal numbers, especially in contexts involving explicit fractions) are the rational numbers that may be expressed as a fraction whose denominator is a power of ten. For example, the decimals represent the fractions , , , and , and are therefore decimal numbers.
More generally, a decimal with n digits after the separator represents the fraction with denominator 10n, whose numerator is the integer obtained by removing the separator.
It follows that a number is a decimal fraction if and only if it has a finite decimal representation.
Expressed as a fully reduced fraction, the decimal numbers are those whose denominator is a product of a power of 2 and a power of 5. Thus the smallest denominators of decimal numbers are
Real number approximation
Decimal numerals do not allow an exact representation for all real numbers, e.g. for the real number . Nevertheless, they allow approximating every real number with any desired accuracy, e.g., the decimal 3.14159 approximates the real , being less than 10−5 off; so decimals are widely used in science, engineering and everyday life.
More precisely, for every real number x and every positive integer n, there are two decimals L and u with at most n digits after the decimal mark such that L ≤ x ≤ u and (u − L) = 10−n.
Numbers are very often obtained as the result of measurement. As measurements are subject to measurement uncertainty with a known upper bound, the result of a measurement is well-represented by a decimal with n digits after the decimal mark, as soon as the absolute measurement error is bounded from above by 10−n. In practice, measurement results are often given with a certain number of digits after the decimal point, which indicate the error bounds. For example, although 0.080 and 0.08 denote the same number, the decimal numeral 0.080 suggests a measurement with an error less than 0.001, while the numeral 0.08 indicates an absolute error bounded by 0.01. In both cases, the true value of the measured quantity could be, for example, 0.0803 or 0.0796 (see also significant figures).
Infinite decimal expansion
For a real number x and an integer n ≥ 0, let [x]n denote the (finite) decimal expansion of the greatest number that is not greater than x that has exactly n digits after the decimal mark. Let di denote the last digit of [x]i. It is straightforward to see that [x]n may be obtained by appending dn to the right of [x]n−1. This way one has
- [x]n = [x]0.d1d2...dn−1dn,
and the difference of [x]n−1 and [x]n amounts to
- ,
which is either 0, if dn = 0, or gets arbitrarily small as n tends to infinity. According to the definition of a limit, x is the limit of [x]n when n tends to infinity. This is written asor
- x = [x]0.d1d2...dn...,
which is called an infinite decimal expansion of x.
Conversely, for any integer [x]0 and any sequence of digits the (infinite) expression [x]0.d1d2...dn... is an infinite decimal expansion of a real number x. This expansion is unique if neither all dn are equal to 9 nor all dn are equal to 0 for n large enough (for all n greater than some natural number N).
If all dn for n > N equal to 9 and [x]n = [x]0.d1d2...dn, the limit of the sequence is the decimal fraction obtained by replacing the last digit that is not a 9, i.e.: dN, by dN + 1, and replacing all subsequent 9s by 0s (see 0.999...).
Any such decimal fraction, i.e.: dn = 0 for n > N, may be converted to its equivalent infinite decimal expansion by replacing dN by dN − 1 and replacing all subsequent 0s by 9s (see 0.999...).
In summary, every real number that is not a decimal fraction has a unique infinite decimal expansion. Each decimal fraction has exactly two infinite decimal expansions, one containing only 0s after some place, which is obtained by the above definition of [x]n, and the other containing only 9s after some place, which is obtained by defining [x]n as the greatest number that is less than x, having exactly n digits after the decimal mark.
Rational numbers
Long division allows computing the infinite decimal expansion of a rational number. If the rational number is a decimal fraction, the division stops eventually, producing a decimal numeral, which may be prolongated into an infinite expansion by adding infinitely many zeros. If the rational number is not a decimal fraction, the division may continue indefinitely. However, as all successive remainders are less than the divisor, there are only a finite number of possible remainders, and after some place, the same sequence of digits must be repeated indefinitely in the quotient. That is, one has a repeating decimal. For example,
- = 0. 012345679 012... (with the group 012345679 indefinitely repeating).
The converse is also true: if, at some point in the decimal representation of a number, the same string of digits starts repeating indefinitely, the number is rational.
| For example, if x is | 0.4156156156... |
| then 10,000x is | 4156.156156156... |
| and 10x is | 4.156156156... |
| so 10,000x − 10x, i.e. 9,990x, is | 4152.000000000... |
| and x is |
or, dividing both numerator and denominator by 6, .
Decimal computation
Most modern computer hardware and software systems commonly use a binary representation internally (although many early computers, such as the ENIAC or the IBM 650, used decimal representation internally). For external use by computer specialists, this binary representation is sometimes presented in the related octal or hexadecimal systems.
For most purposes, however, binary values are converted to or from the equivalent decimal values for presentation to or input from humans; computer programs express literals in decimal by default. (123.1, for example, is written as such in a computer program, even though many computer languages are unable to encode that number precisely.)
Both computer hardware and software also use internal representations which are effectively decimal for storing decimal values and doing arithmetic. Often this arithmetic is done on data which are encoded using some variant of binary-coded decimal, especially in database implementations, but there are other decimal representations in use (including decimal floating point such as in newer revisions of the IEEE 754|IEEE 754 Standard for Floating-Point Arithmetic).
Decimal arithmetic is used in computers so that decimal fractional results of adding (or subtracting) values with a fixed length of their fractional part always are computed to this same length of precision. This is especially important for financial calculations, e.g., requiring in their results integer multiples of the smallest currency unit for book keeping purposes. This is not possible in binary, because the negative powers of have no finite binary fractional representation; and is generally impossible for multiplication (or division). See Arbitrary-precision arithmetic for exact calculations.
Licensing
Content obtained and/or adapted from:
- Radix, Wikipedia under a CC BY-SA license
- Binary number, Wikipedia under a CC BY-SA license
- Quinary, Wikipedia under a CC BY-SA license
- Decimal, Wikipedia under a CC BY-SA license







































![{\displaystyle \left\vert \left[x\right]_{n}-\left[x\right]_{n-1}\right\vert =d_{n}\cdot 10^{-n}<10^{-n+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa97ac58d939553b57b29422c01a1925a436028e)
![{\textstyle \;x=\lim _{n\rightarrow \infty }[x]_{n}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4726bcc43d70340455e0f0340fa72d52ee7e420d)

![{\textstyle \;([x]_{n})_{n=1}^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1ebb69f79147f59b60a7fc1079add44c50c1331)




