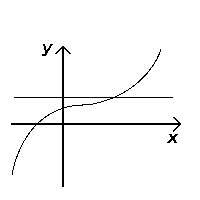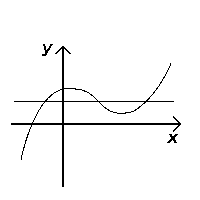Difference between revisions of "One-to-one functions"
Rylee.taylor (talk | contribs) (fixing link to go straight to pdf) |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[File:Function_Definition.svg|alt=The image demonstrates a mapping of some element a (the circle) in A, the domain, to exactly one element b in B, the range.|thumb|<math>A</math> is the domain of the function while <math>B</math> is the range. This transformation from set <math>A</math> to <math>B</math> is an example of one-to-one function.]] | ||
| + | |||
| + | To make it simple, for the function <math>f(x)</math>, all of the possible <math>x</math> values constitute the domain, and all of the values <math>f(x)</math> (<math>y</math> on the x-y plane) constitute the range. To put it in more formal terms, a function <math>f</math> is a mapping of some element <math>a\in A</math>, called the domain, to exactly one element <math>b\in B</math>, called the range, such that <math>f:A\to B</math>. The image below should help explain the modern definition of a function: | ||
| + | |||
| + | : A function is considered '''one-to-one''' if an element <math>a\in A</math> from domain <math>A</math> of function <math>f</math>, leads to exactly one element <math>b\in B</math> from range <math>B</math> of the function. By definition, since only one element <math>b</math> is mapped by function <math>f</math> from some element <math>a</math>, <math>f:A\to B</math> implies that there exists only one element <math>b</math> from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to '''''Figure 1'''''. | ||
| + | |||
| + | ===The horizontal line and the algebraic 1-1 test=== | ||
| + | Similarly, the horizontal line test, though does not test if an equation is a function, tests if a function is injective (one-to-one). If any horizontal line ever touches the graph at more than one point, then the function is not one-to-one; if the line always touches at most one point on the graph, then the function is one-to-one. | ||
| + | |||
| + | [[File:Horizontal-test-ok.png|thumb|A one-to-one function passes the horizontal line test]] | ||
| + | |||
| + | [[File:Horizontal-test-fail.png|thumb|This function does NOT pass the horiontal line test]] | ||
| + | |||
| + | The algebraic 1-1 test is the non-geometric way to see if a function is one-to-one. The basic concept is that: | ||
| + | |||
| + | Assume there is a function <math>f</math>. If:<blockquote><math>f(a)=f(b)</math>, and <math>a=b</math>, then</blockquote>function <math>f</math> is one-to-one. | ||
| + | |||
| + | Here is an example: prove that <math>f(x)=\frac{1-2x}{1+x}</math> is injective. | ||
| + | |||
| + | Since the notation is the notation for a function, the equation is a function. So we only need to prove that it is injective. Let <math>a</math> and <math>b</math> be the inputs of the function and that <math>f(a)=f(b)</math>. Thus, | ||
| + | |||
| + | :<math>\frac{1-2a}{1+a}=\frac{1-2b}{1+b}</math> | ||
| + | :<math>\Leftrightarrow(1+b)(1-2a)=(1+a)(1-2b)</math> | ||
| + | :<math>\Leftrightarrow1-2a+b-2ab=1-2b+a-2ab</math><br><math>\Leftrightarrow1-2a+b=1-2b+a</math> | ||
| + | :<math>\Leftrightarrow1-2a+3b=1+a</math> | ||
| + | :<math>\Leftrightarrow1+3b=1+3a</math> | ||
| + | :<math>\Leftrightarrow a=b</math> | ||
| + | |||
| + | So, the result is <math>a=b</math>, proving that the function is injective. | ||
| + | |||
| + | Another example is proving that <math>g(x)=x^2</math> is not injective. | ||
| + | |||
| + | Using the same method, one can find that <math>a=\pm b</math>, which is not <math>a=b</math>. So, the function is not injective. | ||
| + | |||
| + | ==Resources== | ||
* [https://mathresearch.utsa.edu/wikiFiles/MAT1093/One-to-one%20functions/Esparza%201093%20Notes%201.7.pdf One-to-one functions]. Written notes created by Professor Esparza, UTSA. | * [https://mathresearch.utsa.edu/wikiFiles/MAT1093/One-to-one%20functions/Esparza%201093%20Notes%201.7.pdf One-to-one functions]. Written notes created by Professor Esparza, UTSA. | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Functions Functions], Wikibooks: Calculus | ||
| + | * [https://www.math.uh.edu/~jiwenhe/Math1432/lectures/lecture01_handout.pdf One-to-one Functions and Inverses], University of Houston | ||
| + | |||
| + | ==Licensing== | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikibooks.org/wiki/Calculus/Functions Functions, Wikibooks: Calculus] under a CC BY-SA license | ||
Latest revision as of 12:29, 25 October 2021
To make it simple, for the function , all of the possible values constitute the domain, and all of the values ( on the x-y plane) constitute the range. To put it in more formal terms, a function is a mapping of some element , called the domain, to exactly one element , called the range, such that . The image below should help explain the modern definition of a function:
- A function is considered one-to-one if an element from domain of function , leads to exactly one element from range of the function. By definition, since only one element is mapped by function from some element , implies that there exists only one element from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to Figure 1.
The horizontal line and the algebraic 1-1 test
Similarly, the horizontal line test, though does not test if an equation is a function, tests if a function is injective (one-to-one). If any horizontal line ever touches the graph at more than one point, then the function is not one-to-one; if the line always touches at most one point on the graph, then the function is one-to-one.
The algebraic 1-1 test is the non-geometric way to see if a function is one-to-one. The basic concept is that:
Assume there is a function . If:
, and , then
function is one-to-one.
Here is an example: prove that is injective.
Since the notation is the notation for a function, the equation is a function. So we only need to prove that it is injective. Let and be the inputs of the function and that . Thus,
So, the result is , proving that the function is injective.
Another example is proving that is not injective.
Using the same method, one can find that , which is not . So, the function is not injective.
Resources
- One-to-one functions. Written notes created by Professor Esparza, UTSA.
- Functions, Wikibooks: Calculus
- One-to-one Functions and Inverses, University of Houston
Licensing
Content obtained and/or adapted from:
- Functions, Wikibooks: Calculus under a CC BY-SA license