Difference between revisions of "Trigonometric Functions: Unit Circle Approach"
| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The Unit Circle | + | ==The Unit Circle== |
| + | Consider an angle in standard position, such that the point (''x'', ''y'') on the terminal side of the angle is a point on a circle with radius 1. | ||
| − | [[File: | + | :[[File:Defining Trigonometric Functions Figure 4.svg|500px]] |
| − | + | This circle is called the '''unit circle'''. With ''r'' = 1, we can define the trigonometric functions in the unit circle: | |
| − | {{ | + | {| style="background:transparent;" cellpadding="5" |
| + | | style="padding-right:30px;" | <math>\cos \theta = \frac{x}{r} = \frac{x}{1} = x</math> || <math>\sec \theta = \frac{r}{x} = \frac{1}{x}</math> | ||
| + | |- | ||
| + | | <math>\sin \theta = \frac{y}{r} = \frac{y}{1} = y</math> || <math>\csc \theta = \frac{r}{y} = \frac{1}{y}</math> | ||
| + | |- | ||
| + | | <math>\tan \theta = \frac{y}{x}</math> || <math>\cot \theta = \frac{x}{y}</math> | ||
| + | |} | ||
| − | + | Notice that in the unit circle, the sine and cosine of an angle are the ''x'' and ''y'' coordinates of the point on the terminal side of the angle. Now we can find the values of the trigonometric functions of any angle of rotation, even the quadrantal angles, which are not angles in triangles. | |
| − | |||
| − | |||
| − | |||
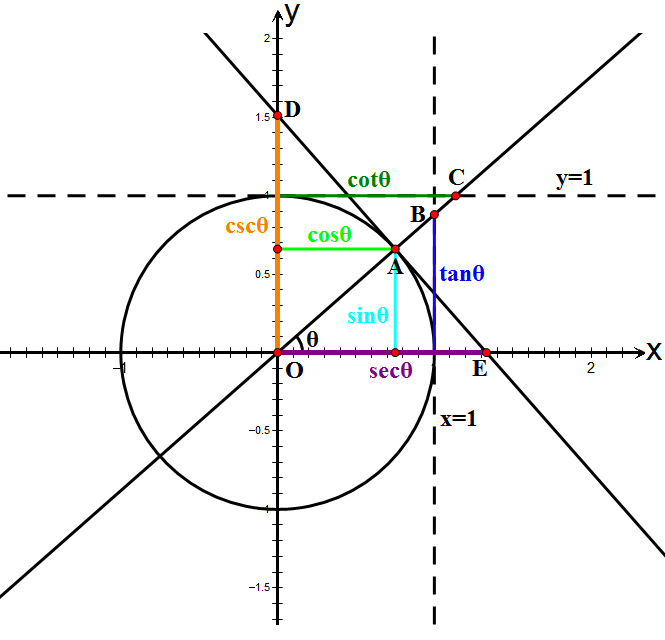
| − | + | [[File:Unit Circle Definitions of Six Trigonometric Functions.png|The center of the unit circle is the origin <math>O</math>, point <math>A=(x_A,y_A)</math>. Creating line segments starting from point <math>A</math> to <math>x</math> on the <math>x</math>-axis will create two line segments. From this, we learn that, in terms of <math>\theta</math>, point <math>A=(\cos\theta,\sin\theta)</math>and other properties.]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math>\ | + | The center of the unit circle is the origin <math>O</math>, point <math>A=(x_A,y_A)</math>. Creating line segments starting from point <math>A</math> to <math>x</math> on the <math>x</math>-axis will create two line segments. From this, we learn that, in terms of <math>\theta</math>, point <math>A=(\cos\theta,\sin\theta)</math>and other properties. |
| − | |||
| − | |||
| − | + | [[File:Unit_circle_angles.svg|Labeled unit circle]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We can use the figure above to determine values of the trig functions for the quadrantal angles. For example, <math>\sin{90^\circ} = y = 1</math>. <math>\sec{45^\circ} = \frac{1}{x} = \frac{2}{\sqrt{2}} = \sqrt{2}</math>. | |
| − | == | + | ===Example 1=== |
| − | + | Use the unit circle above to find each value: | |
| − | + | a. cos 90° | |
| − | |||
| − | + | b. cot 180° | |
| − | |||
| − | + | c. sec 0° | |
| − | + | ---- | |
| − | + | '''Solution''': | |
| − | + | a. cos 90° = 0 | |
| − | + | :The ordered pair for this angle is (0, 1). The cosine value is the ''x'' coordinate, 0. | |
| − | |||
| − | The | + | b. cot 180° is undefined |
| + | : The ordered pair for this angle is (-1, 0). The ratio <math>\tfrac{x}{y}</math> is <math>\tfrac{-1}{0}</math>, which is undefined. | ||
| − | + | c. sec 0° = 1 | |
| + | : The ordered pair for this angle is (1, 0). The ratio is <math>\tfrac{1}{x}</math> is <math>\tfrac{1}{1}</math> = 1. | ||
| − | + | There are several important angles in the unit circle that you will work with extensively in your study of trigonometry: 30°, 45°, and 60°. To find the values of the trigonometric functions of these angles, we need to know the ordered pairs. Let's begin with 30°. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The terminal side of the angle intersects the unit circle at the point <math>\tfrac{\sqrt{3}}{2}, \tfrac{1}{2}</math>. (You will prove this in one of | |
| − | {{ | + | the review exercises.). Therefore we can find the values of any of the trig functions of 30°. For example, the cosine value is the ''x''-coordinate, so cos (30°) = <math>\tfrac{\sqrt{3}}{2}</math>. Because the coordinates are fractions, we have to do a bit more work in order to find the tangent value: |
| − | + | :<math>\tan (30^\circ) = \frac{y}{x} = \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{2} \cdot \frac{2}{\sqrt{3}} = \frac{1}{\sqrt{3}}</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | In the review exercises you will find the values of the remaining four trig functions of this angle. The table below summarizes the ordered pairs for 30°, 45°, and 60° on the unit circle. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Table 1.10 | ||
| + | ! scope="col" | Angle | ||
| + | ! scope="col" | ''x'' coordinate | ||
| + | ! scope="col" | ''y'' coordinate | ||
| + | |- | ||
| + | | 30° || <math>\tfrac{\sqrt{3}}{2}</math> || <math>\tfrac{1}{2}</math> | ||
| + | |- | ||
| + | | 45° || <math>\tfrac{\sqrt{2}}{2}</math> || <math>\tfrac{\sqrt{2}}{2}</math> | ||
| + | |- | ||
| + | | 60° || <math>\tfrac{1}{2}</math> || <math>\tfrac{\sqrt{3}}{2}</math> | ||
| + | |} | ||
| + | |||
| + | We can use these values to find the values of any of the six trig functions of these angles. | ||
| + | |||
| + | ===Example 2=== | ||
| + | Find the value of each function. | ||
| + | |||
| + | a. cos (45°) | ||
| + | |||
| + | b. sin (60°) | ||
| + | |||
| + | c. tan (45°) | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Solution''': | ||
| + | |||
| + | a. cos (45°) = <math>\tfrac{\sqrt{2}}{2}</math> | ||
| + | : The cosine value is the ''x'' coordinate of the point. | ||
| + | |||
| + | b. sin (60°) = <math>\tfrac{\sqrt{3}}{2}</math> | ||
| + | : The sine value is the ''y'' coordinate of the point. | ||
| + | |||
| + | c. tan (45°) = 1 | ||
| + | : The tangent value is the ratio of the ''y'' coordinate to the ''x'' coordinate. Because the ''x'' and ''y'' coordinates are the same for this angle, the tangent ratio is 1. | ||
| Line 95: | Line 104: | ||
==Resources== | ==Resources== | ||
* [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Trigonometric%20Functions_%20Unit%20Circle%20Approach/Esparza%201093%20Notes%202.2.pdf Trigonometric Functions: Unit Circle Approach]. Written notes created by Professor Esparza, UTSA. | * [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Trigonometric%20Functions_%20Unit%20Circle%20Approach/Esparza%201093%20Notes%202.2.pdf Trigonometric Functions: Unit Circle Approach]. Written notes created by Professor Esparza, UTSA. | ||
| + | * [https://en.wikibooks.org/wiki/High_School_Trigonometry/Defining_Trigonometric_Functions Defining Trigonometric Functions], WikiBooks: High School Trigonometry | ||
| + | * [https://en.wikibooks.org/wiki/Trigonometry/The_Unit_Circle The Unit Circle], WikiBooks: Trigonometry | ||
| + | |||
| + | ==Licensing== | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikibooks.org/wiki/Trigonometry/The_Unit_Circle The Unit Circle, WikiBooks: Trigonometry] under a CC BY-SA license | ||
| + | * [https://en.wikibooks.org/wiki/High_School_Trigonometry/Defining_Trigonometric_Functions Defining Trigonometric Functions, WikiBooks: High School Trigonometry] under a CC BY-SA license | ||
Latest revision as of 12:53, 25 October 2021
The Unit Circle
Consider an angle in standard position, such that the point (x, y) on the terminal side of the angle is a point on a circle with radius 1.
This circle is called the unit circle. With r = 1, we can define the trigonometric functions in the unit circle:
Notice that in the unit circle, the sine and cosine of an angle are the x and y coordinates of the point on the terminal side of the angle. Now we can find the values of the trigonometric functions of any angle of rotation, even the quadrantal angles, which are not angles in triangles.
The center of the unit circle is the origin , point . Creating line segments starting from point to on the -axis will create two line segments. From this, we learn that, in terms of , point and other properties.
We can use the figure above to determine values of the trig functions for the quadrantal angles. For example, . .
Example 1
Use the unit circle above to find each value:
a. cos 90°
b. cot 180°
c. sec 0°
Solution:
a. cos 90° = 0
- The ordered pair for this angle is (0, 1). The cosine value is the x coordinate, 0.
b. cot 180° is undefined
- The ordered pair for this angle is (-1, 0). The ratio is , which is undefined.
c. sec 0° = 1
- The ordered pair for this angle is (1, 0). The ratio is is = 1.
There are several important angles in the unit circle that you will work with extensively in your study of trigonometry: 30°, 45°, and 60°. To find the values of the trigonometric functions of these angles, we need to know the ordered pairs. Let's begin with 30°.
The terminal side of the angle intersects the unit circle at the point . (You will prove this in one of the review exercises.). Therefore we can find the values of any of the trig functions of 30°. For example, the cosine value is the x-coordinate, so cos (30°) = . Because the coordinates are fractions, we have to do a bit more work in order to find the tangent value:
In the review exercises you will find the values of the remaining four trig functions of this angle. The table below summarizes the ordered pairs for 30°, 45°, and 60° on the unit circle.
| Angle | x coordinate | y coordinate |
|---|---|---|
| 30° | ||
| 45° | ||
| 60° |
We can use these values to find the values of any of the six trig functions of these angles.
Example 2
Find the value of each function.
a. cos (45°)
b. sin (60°)
c. tan (45°)
Solution:
a. cos (45°) =
- The cosine value is the x coordinate of the point.
b. sin (60°) =
- The sine value is the y coordinate of the point.
c. tan (45°) = 1
- The tangent value is the ratio of the y coordinate to the x coordinate. Because the x and y coordinates are the same for this angle, the tangent ratio is 1.
Resources
- Trigonometric Functions: Unit Circle Approach. Written notes created by Professor Esparza, UTSA.
- Defining Trigonometric Functions, WikiBooks: High School Trigonometry
- The Unit Circle, WikiBooks: Trigonometry
Licensing
Content obtained and/or adapted from:
- The Unit Circle, WikiBooks: Trigonometry under a CC BY-SA license
- Defining Trigonometric Functions, WikiBooks: High School Trigonometry under a CC BY-SA license